树上倍增(LCA)
第2题 [模板] LCA 查看测评数据信息
模板题:求 LCA(最近公共祖先)。
以 1 号节点为树的根。
输入格式
第一行两个正整数 n, m,表示树的节点数和询问的个数。
接下来 n - 1 行,每行两个正整数 u, v,表示树上有一条连接节点 u 和 v 的边。
接下来 m 行,每行两个正整数 u, v,表示询问节点 u 和 v 的最近公共祖先。
对于 40% 的数据,满足 1 ≤ n, m ≤ 100。
对于 60% 的数据,满足 1 ≤ n, m ≤ 104,数据随机生成。
对于 100% 的数据,满足 1 ≤ n, m ≤ 105。
输出格式
输出共 m 行,每行一个整数表示答案。
输入/输出例子1
输入:
5 2
1 2
1 3
2 4
2 5
1 4
5 4
输出:
1
2
样例解释
无
闲笔:笔者于2024.7.19 重新翻回此文章,并以此做修改
详解
主要讲一下深度做法
思路:
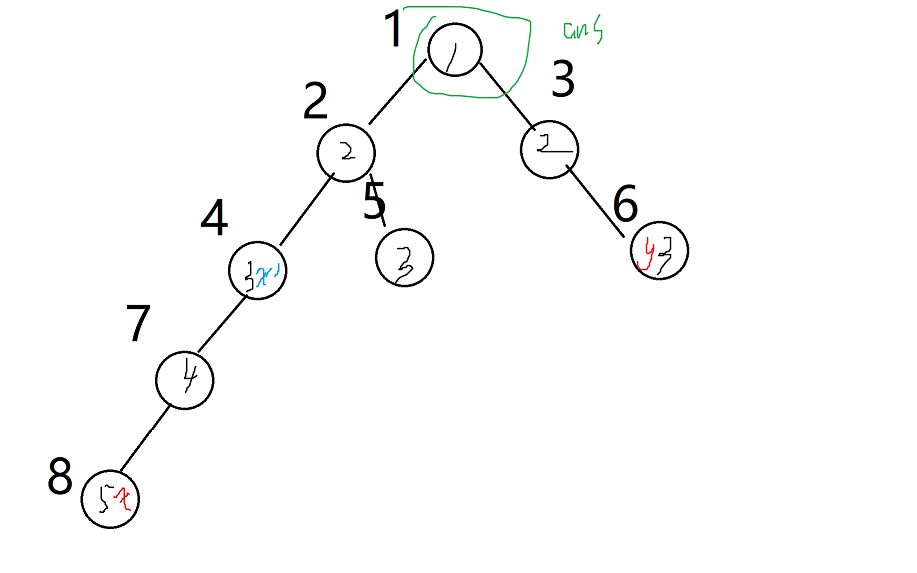
以此图为例,图中节点中心数字为深度(dep),旁边的数字为编号。我们现在要求x与y的最近公共祖先(ans,也就是1)
1.先把x,y抬到同一高度,最终有dep[x]==dep[y],即x到了x',图中蓝色地方
注意,如果此时x和y是同一个点,那么答案就出来了,就是这个点
2.x,y同时往上跳,最终到深度为2的节点,此时深度为2的节点的父亲就是所求
对于第1步,我们要预处理dep,这个跑一遍dfs即可。
但是我们要能以O(1)时间内知道x跳多少步能到什么节点,也就是预处理
一步一步暴力来看太慢了,采用倍增的思想,每次跳2^k步,可以优化很多时间,对于为什么是对的,可以看下面的解释
定 f[i][j] 表示 i节点跳2^j步,能到的节点.这样我们就可以dfs的时候处理一下了,可以理解为dp
初始化很好想,f[u][0]=fa,即一个节点的孩子节点跳2^0步可以到这个节点
转移方程:我们可以折半来想,跳2^j步换一种方式表示
2^j = 2^(j-1)*2 = 2^(j-1) + 2^(j-1)
那么我们可以推出
f[i][j] = f[ f[i][j-1] ][j-1]
对于第2步,我们不能直接跳到他们的LCA节点,可能会误判,注意这点之后直接做就好,具体为什么可以看下面的解释
模拟一下这个图求LCA;
第一步:x : 8 -> 4
第二步:(x)4 -> 2 (y)6 -> 3
输出答案 f[2][0] = 1
一些问题和解释
为什么每次跳2^k步可以正好跳到目标点?为什么跳的时候k从大往小试?
我们先解释后者。
从小向大跳,5≠1+2+4,所以我们还要回溯一步,然后才能得出5=1+4
而从大向小跳,直接可以得出5=4+1。
这也可以拿二进制为例,5(101),从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填,否则就填上,这个过程是很好操作的。
解释完后者,前者也就出来了。
任何数都可以用二进制表示,例如:13,他的二进制就是8+4+1即1101,我们从大往小去试,一定试可以得出
例子:
64>13,跳过
32>13,跳过
16>13,跳过
8<13,我们选择8,此时还差5
4<5,我们选择4,此时还差1
2>1,跳过
1<=1,我们选择1,此时凑齐了
所以,13=8+4+1
所以不用担心跳过头的情况。
为什么x,y一起跳的时候要跳到最近公共祖先点的下面一个点,也就是儿子节点?
如果x,y想要一开始就跳到最近公共祖先,那么可能会成为公共祖先,但不是“最近”,因为无法确定那个节点是最近的
但是如果跳到最近公共祖先的儿子节点,这是很好判断的,因此此时x和y肯定不在同一个点上,就有 f[x][i] != f[y][i] ,那么一定能正确找到“最近”公共祖先
Code
#include <bits/stdc++.h>
using namespace std;
const int N=500005, M=22;
int n, m, u1, v1, root, dep[N], f[N][M];
vector<int> a[N];
void dfs(int u, int fa)
{
dep[u]=dep[fa]+1;
f[u][0]=fa;
for (int i=1; i<=20; i++)
f[u][i]=f[f[u][i-1]][i-1];
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v!=fa) dfs(v, u);
}
}
int lca(int x, int y)
{
if (dep[x]<dep[y]) swap(x, y);
for (int i=20; i>=0; i--)
if (dep[f[x][i]]>=dep[y]) x=f[x][i];
if (x==y) return x;
for (int i=20; i>=0; i--)
if (f[x][i]!=f[y][i]) x=f[x][i], y=f[y][i];
return f[x][0];
}
int main()
{
scanf("%d%d%d", &n, &m, &root);
for (int i=1; i<n; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back(v1);
a[v1].push_back(u1);
}
dfs(root, -1);
while (m--)
{
scanf("%d%d", &u1, &v1);
printf("%d\n", lca(u1, v1));
}
return 0;
}
用法/总结
复杂度分析
基于倍增,LCA函数是O(logn)的复杂度的,预处理也就是O(n)内完成,如果有q次询问,那总体就是 O(n+qlogn)
求树上两点的距离
LCA可以求树上两点间的距离,例如求A,B间的距离,就是 dep[A]+dep[B]-2*dep[lac(A, B)] (备注:这样算是dep[root]=0的情况)
例如下图:

算A,B的距离,就是A到根节点的距离(绿线)+B到根节点的距离(蓝线)- AB的公共祖先到根节点的距离*2(紫线)
因为我们只需要算A,B的距离,不用算A,B到根节点的距离,所以减去AB公共祖先到根节点的距离即可,注意乘上二,因为A,B分别都要减去一次。
如果你根节点的dep值是1,那么算式是:(dep[x]+dep[y]-1*2)-2*(dep[lca(x, y)]-1)
例题:https://www.luogu.com.cn/problem/P10076
技巧总结
一些题目用LCA做,都类似于”树上容斥”,因为树上两点间路径唯一,先加总体再减重复(最近公共祖先之前即为重复)。
之前的文章
以下内容为之前写的了,可以不用看了,不过可以看看时间戳的做法,也挺详细的。
深度做法:
#include<bits/stdc++.h>
using namespace std;
int h[1000005],f[500005][20],n,m,s,x,y,k,dep[1000005];
struct vv{
int r,pre;
}d[1000005];
void cun(int x,int y){
d[++k].r=y;
d[k].pre=h[x];
h[x]=k;
}
void dfs(int x,int y){
dep[x]=dep[y]+1;
for(int i=h[x];i;i=d[i].pre){
int j=d[i].r;
if(j==y) continue;
f[j][0]=x;
for(int k=1;(1<<k)<=dep[x];k++){
f[j][k]=f[f[j][k-1]][k-1];
}
dfs(j,x);
}
}
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=19;i>=0;i--){
if(dep[f[x][i]]>=dep[y]){
x=f[x][i];
}
}
if(x==y) return y;
for(int i=19;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
int main(){
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<n;i++){
scanf("%d%d",&x,&y);
cun(x,y); cun(y,x);
}
dfs(s,0);
while(m--){
scanf("%d%d",&x,&y);
int tem=lca(x,y);
printf("%d\n",tem);
}
return 0;
}
解释1:https://www.luogu.com.cn/problem/solution/P3379 (第一篇题解详细解释,按深度做)
解释2:按时间戳做
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5, M=32;
int n, m, u1, v1, vis[N], f[N][M], cnt=0;
//vis[i]:节点i访问时间
//f[i][j]:从节点f,走2^j步,能到的点
vector<int> a[N];
void dfs(int u, int fa) //u:当前节点 fa:他的父亲节点
{
vis[u]=++cnt; //访问时间
f[u][0]=fa; //u点走1步到父亲
for (int i=1; i<=20; i++) //2^20就行,看题目范围
f[u][i]=f[f[u][i-1]][i-1]; //拆两半,u节点跳2^i步=u节点跳2^(i-1)步+u节点跳2^(i-1)步=f [ f[u][i-1] ] [i-1]
//意思是u的2^i祖先等于u的2^(i-1)祖先的2^(i-1)祖先
//2^i = 2^(i-1) + 2^(i-1)
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v!=fa) dfs(v, u);
}
}
int lca(int u, int v)
{
if (vis[u]>vis[v]) swap(u, v); //保证v访问时间是大的
if (u==v) return u; //别忘了加
for (int i=20; i>=0; i--)//从后往前推。原因如下
//从小向大跳,5≠1+2+4,所以我们还要回溯一步,然后才能得出5=1+4;而从大向小跳,直接可以得出5=4+1。这也可以拿二进制为例,5(101),从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填,这个过程是很好操作的。
if (vis[f[v][i]]>vis[u]) //见下 解释1
v=f[v][i];
return f[v][0]; //距离u,v最近公共祖先还差一步
}
int main()
{
scanf("%d%d", &n, &m);
for (int i=1; i<n; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back(v1);
a[v1].push_back(u1);
}
dfs(1, 1); //这里定1号节点的父亲节点是自己
while (m--)
{
scanf("%d%d", &u1, &v1);
printf("%d\n", lca(u1, v1));
}
return 0;
}
解释1
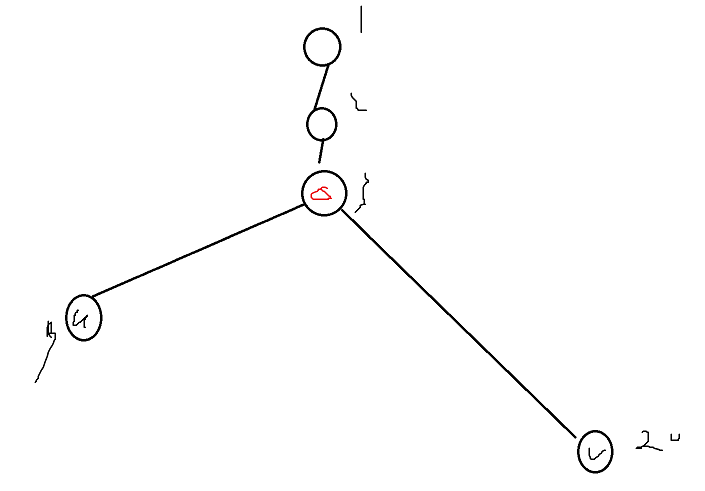
例如这张图,u,v最近公共祖先是三角型那里
有一些二分的思想(v点时间必须>u点时间,且>三角型点时间)
v点先尝试跳64步,发现不行,跳32步.....一直到跳16步,才可以比三角形大,也比u大(因为先根遍历,所以那个点时间必然>u时间)
发现可行就抬高,然后最终就一定会在三角形点的下面一个点
会不会跳过头?
https://www.cnblogs.com/didiao233/p/18000595
最后一段(文章末尾,文字)

