gold(状压+Floyd)

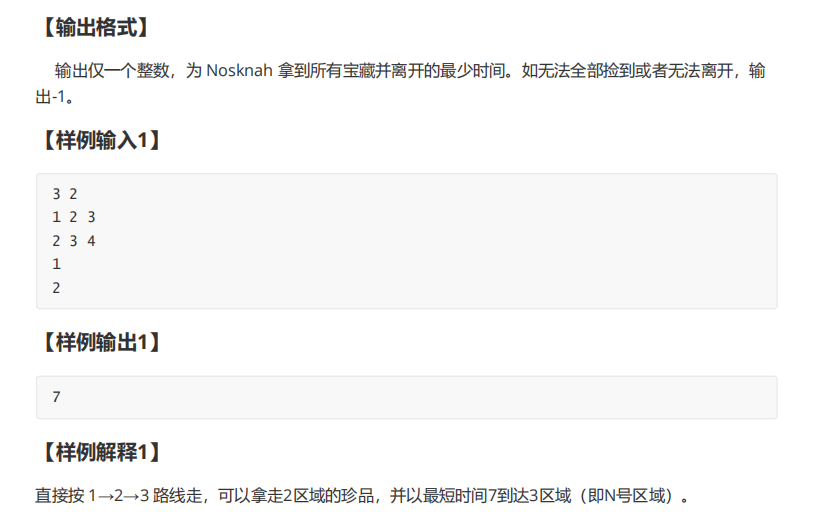
简化题意:1走到n,至少经过指定的p个点(x)的最短路。我们分解一下问题,1~x1~x2...~xp~n
分解为1~x1,x1~x2~...~xp,xp~n
1~x1是已知的,可以作为初始化条件,而后两个不知道,所以我们开数组,用两维表示
f["abcdef"]["f"]表示从1出发,拿完"abcdef",且停在f点,则最后拿的是f,最少的时间
这样就知道x1~x2~...~xp的最短时间,然后xp~n的最短时间也可以求出来,但是不能存字符串,于是考虑用状压
1表示有,0表示无。由于要知道某个点到另外某个点的距离,于是我们用Floyd预处理出每点间的最短路
注意一下数据范围,要开long long
状态转移方程推理过程,假设i是起点(前i个点),j是中转点,k是终点
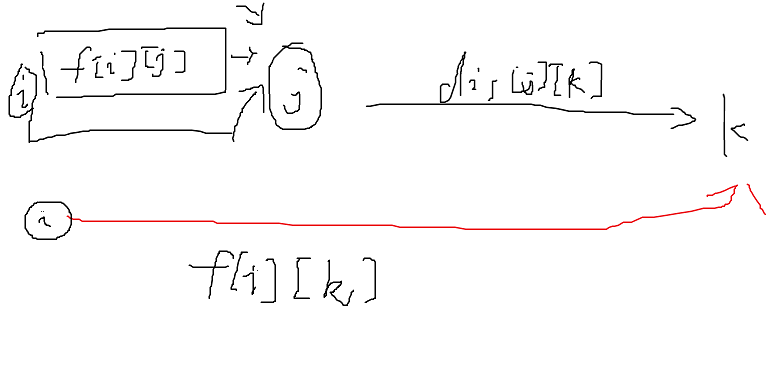
画图分析一下就是,很像松弛!每次都会找最优情况
i->j->k的路径表示为 f[i][j]+dis[j][k]
i->k的路径表示为f[i][k]
然后更新i->k的路径为两者的最小值
于是转移方程出来了
f[i][k]=min(f[i][j]+dis[x[j]][x[k]], f[i][k])
#include <bits/stdc++.h>
using namespace std;
const int N=2005, M=13;
int n, m, u, v, p, x[N];
long long dis[N][N], w, f[(1<<M)][M], tot=0, ans=1e18;
long long min2(long long a, long long b)
{
if (a<b) return a;
return b;
}
int main()
{
scanf("%d%d", &n, &m);
memset(dis, 63, sizeof dis);
for (int i=1; i<=m; i++)
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
dis[u][v]=dis[v][u]=min2(dis[u][v], w);
dis[u][u]=dis[v][v]=0;
}
scanf("%d", &p);
for (int i=1; i<=p; i++) scanf("%d", &x[i]);
for (int k=1; k<=n; k++)
for (int i=1; i<=n; i++)
for (int j=1; j<=n; j++)
if(dis[k][j]!=dis[0][0] && dis[i][k]!=dis[0][0] && i!=j && j!=k && i!=k)
dis[i][j]=min2(dis[i][j], dis[i][k]+dis[k][j]);
//预处理最短路
memset(f, 63, sizeof f);
for (int i=1; i<=p; i++)
f[1<<(i-1)][i]=dis[1][x[i]]; //1至(1~p)的距离,初始化
tot=(1<<p)-1; //总宝藏数
for (int i=1; i<=tot; i++) //前i个宝藏-集合
for (int j=1; j<=p; j++) //j:中转点
if (i&(1<<(j-1))) //i包含 j ,因为要在i集合(要走的点)里面选一个中转点
{
for (int k=1; k<=p; k++) //k:目标点
if (j!=k) //中转点不等于目标点
{
//于是在i集合补k,就是走完后的结果
f[i|(1<<(k-1))][k]=min2(f[i|(1<<(k-1))][k], f[i][j]+dis[x[j]][x[k]]);
}
}
for (int i=1; i<=p; i++)
ans=min2(ans, f[tot][i]+dis[x[i]][n]); //走完后停留的点~n的距离
if (ans<1e18) printf("%lld", ans);
else printf("-1");
return 0;
}
/*
3 2
1 2 3
2 3 4
1
2
*/
csh:
对于一个最短路新手小白来说,一眼看去,只想暴力,重复调用dj(Dijkstra简称),10分over。这个数据很显然可以看出不能每次都去重算最短路,这样很浪费时间,那么要是一步一步从前一步推过来,就会很方便,用已知的去刷新未知的。
lgj:有点dp的味道了
那怎么表示状态呢?必备的一维是当前的位置,因为这样才能从前一步推过来,还有一维就是拿了什么宝藏,走的越多,走的越后,宝藏个数越多。这两个条件就保证了无后效性。 一共需要三个for,最外层枚举拿了什么物品,问题来了,如何表示拿了什么宝藏这个状态?--这就要用到恶心又好用的状压,用二进制表示,0是当前位的宝藏没拿,1是拿了,每个位就是按顺序的宝藏,求出p个宝藏拿与不拿的所有情况,从1开始枚举(宝藏肯定是拿的越多,走的路越多,所有按照宝藏的个数,事实上就是顺应了前面说的,可以从前一步推过来)。第二个枚举现在的停留点,第三个枚举前一个点,现在的最短路就等于前一个点的最短路加上前一个点到现在的点的最短路。前一个点到现在的点的最短路就可以用Floyd,在前面预处理出两点之间的距离。
最后还要回到n点,同理,现在n是当前点,枚举前一个点,但注意是拿完宝藏之后立马走,所以最后枚举的前一个点必须是有宝藏的点。
写代码时还要注意一下最大值(非常大才能过,因为这个调了半天)的大小以及做加法时会不会爆。
#include<bits/stdc++.h>
using namespace std;
long long n,m,x,y,w,p,a[13],mp[205][205],tot,b[15],f[1<<13][13],mi=1e12,oo=0x3f;
//第一个为拿走了什么宝藏,状态二进制表示 ,第二个为 停留在什么宝藏
int main()
{ scanf("%lld%lld",&n,&m);
memset(mp,0x3f,sizeof(mp));
oo=mp[0][0];
for(int i=1;i<=n;i++)
mp[i][i]=0;
for(int i=1;i<=m;i++)
{ scanf("%lld%lld%lld",&x,&y,&w);
mp[x][y]=mp[y][x]=min(mp[x][y],w);//mp存的是位置
}
scanf("%lld",&p);
for(int i=1;i<=p;i++)
scanf("%lld",&a[i]);//只有珍品才不对应,区域叫什么就是什么
for(int k=1;k<=n;k++)//Floyed
{ for(int i=1;i<=n;i++)
{ for(int j=1;j<=n;j++)
if(mp[i][k]==oo||mp[k][j]==oo)
continue;
else
if(mp[i][j]>mp[i][k]+mp[k][j])
mp[i][j]=mp[i][k]+mp[k][j];
}
}
tot=(1<<p)-1;
memset(f,0x3f,sizeof(f));
for(int i=1;i<=tot;i++)
{ int s=0;
for(int j=1;j<=p;j++)//选宝藏
{ if((1<<(j-1)&i)!=0)
b[++s]=j;
}
if(s==1)
{
f[i][b[1]]=mp[1][a[b[1]]];
continue;
}
for(int j=1;j<=s;j++)//枚举停留点
{
for(int k=1;k<=s;k++)//子问题,找前一个点
{
if(j==k)continue;
if(f[i-(1<<(b[j]-1))][b[k]]!=oo&&mp[a[b[j]]][a[b[k]]]!=oo)
f[i][b[j]]=min(f[i][b[j]],f[i-(1<<(b[j]-1))][b[k]]+mp[a[b[j]]][a[b[k]]]);
}
}
}
for(int i=1;i<=p;i++)//枚举倒数第二个点,从那里走到n
{ if(f[tot][i]!=oo&&mp[a[i]][n]!=oo)
mi=min(mi,f[tot][i]+mp[a[i]][n]);
}
if(mi==1e12)cout<<-1;
else cout<<mi;
/*
3 2
1 2 3
2 3 4
1
2
*/
return 0;
}

