Python函数和代码复用
(1).函数的定义与使用
1)函数的定义与使用方法
函数是一段代码的表示,它对应了一段具有特定功能的、可重用的语句组,它是一种功能的抽象,它表达特定的含义。在一般编程中,函数有两个作用,它通过函数定义一段功能,可以降低编码难度,同时也可以对一段代码进行复用。
函数的使用方法如下,其中函数体指的是函数内部包含的一些语句代码:
def <函数名>(<参数(0个或多个)>):
<函数体>
return <返回值>
实例:计算n!
def fact(n):
s=1
for i in range(1,n+1):
s*=i
return s
函数在定义时,所指定的参数只是一种占位符,它是一种符号表示。函数定义之后,如果这个函数不被调用,那么这个函数在程序中也是不会被执行,即函数被调用才会执行。
从另外一个角度来理解函数,函数在定义时给定参数,参数就是函数的输入,函数体本身就是对参数的一种处理,而return就是给出这段函数运行的结果,可以看到有输入、处理和输出,这就是IPO。可以简单理解函数就是IPO的一种实现,函数也是一段完整代码的封装。
2)函数的使用以及调用过程
函数的调用指的是运行函数代码的方式,例如上面的实例计算n!,程序看到这段定义并不会去执行这段代码,而执行需要使用函数的调用方式。所谓调用就是用函数的名称给定一个具体的值作为参数,所以调用时给出的实际参数是运行函数的输入,要用实际的参数替换定义中的占位参数,函数调用后会得到实际参数运行之后的运行结果。
以如下代码为例,说明调用过程:
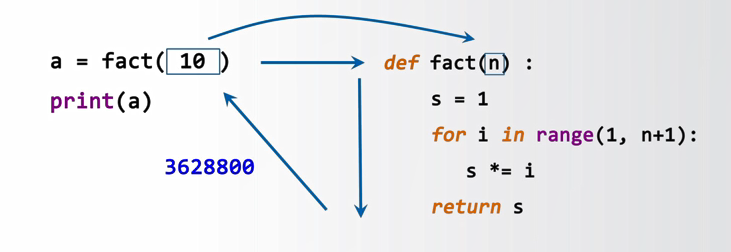
首先,程序会查找定义的函数fact,并将给定的参数10赋给这个函数的占位参数n,此时10就代替了定义函数中的n。然后执行函数体相关的程序,那么运算这段代码之后产生了一个具体的s值。接着这个具体的s值会被作为返回值返回给fact(10)的这段代码,作为运算结果并赋值给变量a。最后print(a)之后,得到了整个10!的运算结果。这就是一个函数的调用过程
3)函数的参数传递
其实函数可以有参数,也可以没有参数,但是无论函数定义时有没有参数都必须保留这个括号,如果没有参数直接给个空括号,格式如下(没有参数):
def <函数名>():
<函数体>
return <返回值>
此外,在函数定义时也可以为某些参数指定一个默认值,构成可选参数。可选参数就是在调用函数时,某些可以提供也可以不提供的参数。Python中要求在定义函数时,所有的可选参数必须放在必选参数之后,这是一种约定。此时的格式如下:
def <函数名>(<必选参数>,<可选参数>):
<函数体>
return <返回值>
说明:可选参数格式为<参数名称>=<默认值>,例如:
def fact(n,m=1):
s=1
for i in range(1,n+1):
s*=i
return s//m
在上面这个函数中,m就是可选参数,默认值为1。当调用参数fact(10)时,返回3628800;当调用参数fact(10,5)时,返回725760。这叫可选参数传递。
此外在参数传递中,还有一种叫可变参数传递,也就是说在定义函数时,可以设计函数接收的参数时可变数量的,即不确定参数总数量。此时的格式如下:
def <函数名>(<参数>,*<参数>):
<函数体>
return <返回值>
例如:
def fact(n,*m):
s=1
for i in range(1,n+1):
s*=i
for j in m:
s*=j
return s
在上面这个函数中,m就是可变参数。当调用参数fact(10,3)时,返回10886400;当调用函数fact(10,3,5,8)时,返回435456000;甚至可以给出更多的参数。
说到可变参数传递就不能不说max()函数和min()函数,他们就是使用可变参数来进行参数的定义。
参数的传递指的是在函数调用时,参数可以按照位置或名称方式传递。这里以可选参数的例子进行说明:
def fact(n,m=1):
s=1
for i in range(1,n+1):
s*=i
return s//m
可以使用fact(10,5)调用函数,使用的是位置传递,10对应占位参数n,5对应占位参数m。也可以使用fact(m=5,n=10)调用函数,使用的是名称传递,直接指定占位参数的实际值。
4)函数的返回值
函数可以返回0个或多个结果,其中使用保留字return来传递返回值。但其实函数可以有返回值,也可以没有,可以使用保留字return,也可以不使用。一段函数如果不想返回任何值,可以给出return但不加任何的返回信息,也可以不适用return,所以return并不是定义函数的必要保留字。return可以传递0个返回值,也可以传递任意多个返回值。
例如:
def fact(n,m=1):
s=1
for i in range(1,n+1):
s*=i
return s//m,n,m
当使用fact(10,5)调用函数时,那么将返回(725760, 10, 5),返回值使用小括号包裹中间用逗号隔开的形式来体现,即元组类型。当然在使用过程中,也可以用对应数量的变量名来分别获取函数的返回值,将返回值赋值给变量,例如a,b,c=fact(10,5),那么a=725760,b=10,c=5。
5)局部变量和全局变量
局部变量是函数内部使用的变量,而函数外部整个程序使用的变量叫全局变量。例如:
n,s=10,100 #这里的n和s是全局变量
def fact(n): #这里的n是局部变量
s=1 #这里的s是局部变量
for i in range(1,n+1):
s*=i
return s
print(fact(n),s) #这里的n和s是全局变量
在函数中,无论是参数还是内部使用的变量都是局部变量。
局部变量和全局变量的使用规则有两点。第一点,局部变量和全局变量是不同的变量,局部变量是函数内部的占位符,与全局变量可能重名但不同。并且在函数运算结束后局部变量被释放,也就是说这个变量将不再存在。当然可以使用保留字global在函数内部使用全局变量。这里举一个在函数内部使用全局变量的例子,如下:
n,s=10,100
def fact(n):
global s #声明此处s是全局变量s
for i in range(1,n+1):
s*=i
return s
print(fact(n),s) #此时输出的s已经被函数修改
第二点,如果局部变量是组合数据类型(序列类型(字符串、元组、列表)、集合类型(集合)、映射类型(字典)),而且未在函数内部创建,那么它就是全局变量。例如:
ls=["F","f"] #创建一个全局变量列表ls
def func(a):
ls.append(a) #此处ls是列表类型,并且未在函数内部创建,则等同于全局变量
return
func("C") #全局变量ls被修改
print(ls) #输出结果['F','f','C']
当在函数内部创建组合数据类型是,如下:
ls=["F","f"] #创建一个全局变量列表ls
def func(a):
ls=[] #此处真实创建了局部变量列表ls
ls.append(a)
return
func("C") #局部变量ls被修改,而全局变量ls没有被修改
print(ls) #输出结果['F','f']
这样造成的原因是:在Python中组合数据类型是由指针来体现的,所以函数中如果没有真实创建组合数据类型,它使用的变量是使用的指针,而指针是外部的全局变量,所以在修改这个指针对应的内容时就修改了全局变量。
6)lambda函数
lambda函数能够返回一个函数名作为结果,简单来说lambda函数是一种匿名函数。它使用lambda保留字来定义,函数名就是返回结果。lambda函数仅用于定义一种简单的,能够在一行内表达实现的一种函数。使用格式如下:
<函数名>=lambda <参数>:<表达式>
#等价于
def <函数名>(<参数>):
<函数体>
return <返回值>
注意:lambda函数后面只能使用表达式,而不能使用函数体。
实例:
>>> f=lambda x,y:x+y >>> f(10,15) 25
当然lambda函数也可以接收没有参数的函数,例如:
>>> f=lambda :"lambda函数" >>> f() 'lambda函数' >>> print(f()) lambda函数
一般在编写代码时,哪怕这个函数只有一行,也建议使用def和return这种方法来定义,要谨慎使用lambda函数。
lambda函数不是定义函数的常用形式,它的存在主要是用作一些特定的函数或方法的参数,有一些非常复杂的函数,它的某一个参数就是一个函数,这种情况下使用lambda函数。
lambda函数有一些固定使用方法,建议逐步掌握。一般情况下建议使用def定义普通函数,不要使用lambda函数这种形式。
(2).代码复用与函数递归
1)代码复用与模块化设计
我们可以把编写的代码当做一种资源,并且对这种资源进一步抽象,实现代码的资源化和抽象化。代码资源化指的是程序代码本身也是一种表达计算的资源,代码抽象化指的是使用函数等方法对代码赋予更高级别的定义。对同一份代码在需要时被重复使用就构成了代码复用,而代码复用是需要将代码进行抽象才能达到的效果。
在不同的程序设计语言中,都有代码复用的相关功能。一般来说,我们使用函数和对象这两种方法来实现代码复用。可以认为这两种方法是实现代码复用的方法,也可以认为这两种方法是对代码进行抽象的不同级别。函数能够命名一段代码,在代码层面建立初步抽象,但这种抽象级别比较低,因为它只是将代码变成了一个功能组。对象通过属性和方法,能够将一组变量甚至一组函数进一步进行抽象。
在代码复用的基础上,我们可以开展模块化设计。模块化设计是基于一种逻辑的设计思维,它的含义是通过封装函数或对象将程序划分为模块以及模块之间的表达。对于要实现的算法,如果设定了功能模块并且在功能模块之间建立关系,那么一个程序就能够被表达清楚。
在模块化设计的思想中,需要关注一个程序的主程序、子程序和子程序之间的关系。我们一般将子程序看做模块,主程序看做模块与模块之间的关系。可以认为模块化设计是一种分而治之、分层抽象、体系化的设计思想。
模块化设计有两个基本概念:紧耦合和松耦合。紧耦合是指两个部分之间交流很多,无法独立存在,那么这两个部分就是紧耦合;松耦合指的是两个部分之间交流很少,它们之间有非常清晰简单的接口,可以独立存在,这就是松耦合。
一般编写程序时,通过函数来将一段代码与代码的其他部分分开,那么函数的输入参数和返回值就是这段函数与其他代码之间的交流通道,这样的交流通道越少越清晰,那么定义的函数复用可能性就越高。所以在模块化设计过程中,对于模块内部,也就是函数内部,近可能的紧耦合,它们之间通过局部变量可以进行大量的数据传输。但是在模块之间,也就是函数与函数之间要尽可能减少它们的传递参数和返回值,让它们之间以松耦合的形式进行组织,这样每一个函数才有可能被更多的函数调用,它的代码才能更多的被复用。
2)函数递归的理解
在函数定义中,调用函数自身的方式就是递归。递归并不是程序设计的专有名词,在数学中也广泛存在,例如:n!。在n!中,我们定义当n=0时,n!为1;除此之外,其余n!=n*(n-1)!这就是一种递归形式。
在递归的定义中有两个关键的特性:链条和基例。链条指的是在递归定义中,它的计算过程是存在一种递归有序的链条关系,例如:n!=n*(n-1)!,那么n!与(n-1)!就构成了递归链条。基例指的是存在一个或多个不需要再次递归的实例,例如:当n=0时,定义n!的值为1,这就是一种基例,它与其它的值之间不存在递归关系,它已是递归的最末端。这两种关键特性就构成了递归的定义,缺少任意一个都构不成递归。在数学中被成为数学归纳法,递归也可以认为是数学归纳法思维在编程中的一种体现。
3)函数递归的调用过程
这里直接通过一个例子n!来看函数递归的调用过程,如下:
def fact(n):
if n==0:
return 1
else:
return n*fact(n-1)
可以看到要实现递归需要利用函数与分支语句进行组合。首先递归本身就是一个函数,因为它需要调用自身,如果不通过函数来定义,那么很难调用自身。接着在函数内部,需要区分基例和链条,所以要使用一个分支语句对输入参数进行判断,如果输入参数是基例的参数条件,我们就要给出基例的代码,如果不是基例的参数条件,我们要用链条的方式表达这种递归关系。
当调用fact(n)函数时,需要给出一个参数,例如n=5。当n=5时,会返回n*fact(n-1),也就是5*fact(4)。fact(4)又调用了函数fact(n),返回4*fact(3)。依次往下,知道调用到fact(0),满足基例,返回1。之后再依次回推,直到得到最终答案。
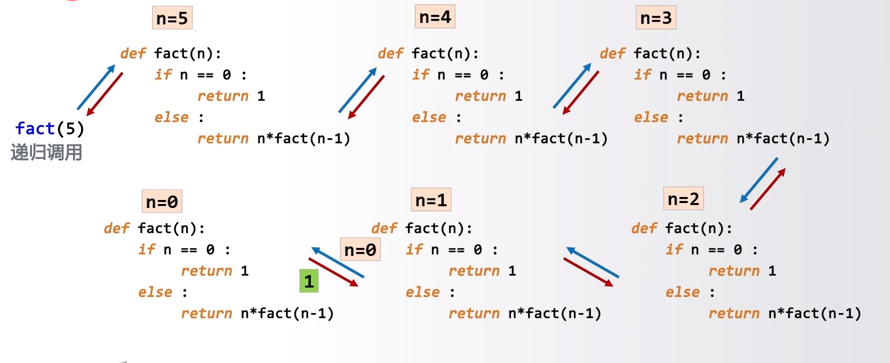
计算机调用函数会开辟内存,将函数内容复制进来,代入参数进行运算。递归看起来是调用了同一个函数,但在计算机内存中并不一样,会不停的开辟内存、复制函数、代入参数运算。
4)函数递归实例解析
实例1:字符串反转。将字符串反转后输出
def rvs(n):
if s=="":
return s
else:
return rvs(s[1:])+s[0]
实例2:斐波那契数列。当n=1或2时,F(n)=1;当n>2,且为整数时,F(n)=F(n-1)+F(n-2)。
def F(n):
if s==1 or s==2:
return 1
else:
return F(n-1)+F(n-2)
实例3:汉诺塔问题
count=0
def hanoi(n,src,dst,mid):
global count
if n==1:
print("{}:{}->{}".format(1,src,dst))
count+=1
else:
hanoi(n-1,src,mid,dst)
print("{}:{}->{}".format(n,src,dst))
count+=1
hanoi(n-1,mid,dst,src)
hanoi(3,"A","B","C")
print(count)
#数据结果为
1:A->B
2:A->C
1:B->C
3:A->B
1:C->A
2:C->B
1:A->B
7


 浙公网安备 33010602011771号
浙公网安备 33010602011771号