牛客 小白112 20250326

牛客 小白112 20250326

https://ac.nowcoder.com/acm/contest/103957

A：
题目大意：天平一端有 \(w\) 重的物品，给定砝码 \(a,b\) 判断能否是天平平衡

#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18
#define Iinf 2e9
#define LL long long
#define ULL unsigned long long 

using namespace std;

void solve(){
	int a,b,w;
	cin>>a>>b>>w;
	if (a+b==w||max(a,b)-min(a,b)==w||a==w||b==w)
		cout<<"Yes"<<endl;
	else
		cout<<"No"<<endl;
}

int main()
{
	cintie;
	solve();
	
	return 0;
}

考虑 \(3\) 种情况，加起来刚好等于 \(w\)，其中一个砝码直接等于 \(w\) ，或者较重的砝码等于 \(w\) 加上另一个砝码

B：

题目大意：给定数组 \(a\) ，定义山峰为某个位置 \(i\) 上满足 \(a_{i-1}<a_i,a_{i+1}>a_i\) ，记这个位置上的山峰高度为

\[h_i=a_i-\lfloor \frac{a_{i-1}+a_{i+1}}{2}\rfloor \]

计算出这个数组中最高的山峰，如果不存在输出 \(-1\)

#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18
#define Iinf 2e9
#define LL long long
#define ULL unsigned long long 

using namespace std;

int n;
int a[100010];

void solve(){
	cin>>n;
	for (int i=1;i<=n;i++) cin>>a[i];
	int ans=0;
	for (int i=2;i<=n-1;i++){
		if (a[i-1]<a[i]&&a[i+1]<a[i])
			ans=max(ans,a[i]-(a[i-1]+a[i+1])/2);
	}
	if (ans) cout<<ans;
	else cout<<-1;
}

int main()
{
	cintie;
	solve();
	
	
	return 0;
}

简单模拟即可，签到

C：

题目大意：有 \(n\) 个球 \(m\) 个桶，当一个桶中的球个数为 \(k\) 个时，桶中的 \(k\) 个球被消除，判断最后剩余的球能否为 \(q\)

#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18
#define Iinf 2e9
#define LL long long
#define ULL unsigned long long 

using namespace std;

LL n,m,k,q;

void solve(){
	cin>>n>>m>>k>>q;
	if ((n-q)%k==0&&q<=m*(k-1))
			cout<<"Yes"<<endl;
	else
		cout<<"No"<<endl;
}

int main()
{
	cintie;
	Trd;
	
	
	return 0;
}

考虑被消除的球数 \(n-q\) 能否由整数次消除 \(k\) 个球构成，即 \(n-q\) 是否能被 \(k\) 整除

然后判断需要保留的 \(q\) 个球桶中是否能装得下，所有桶中最多能存 \((k-1)*m\) 个球

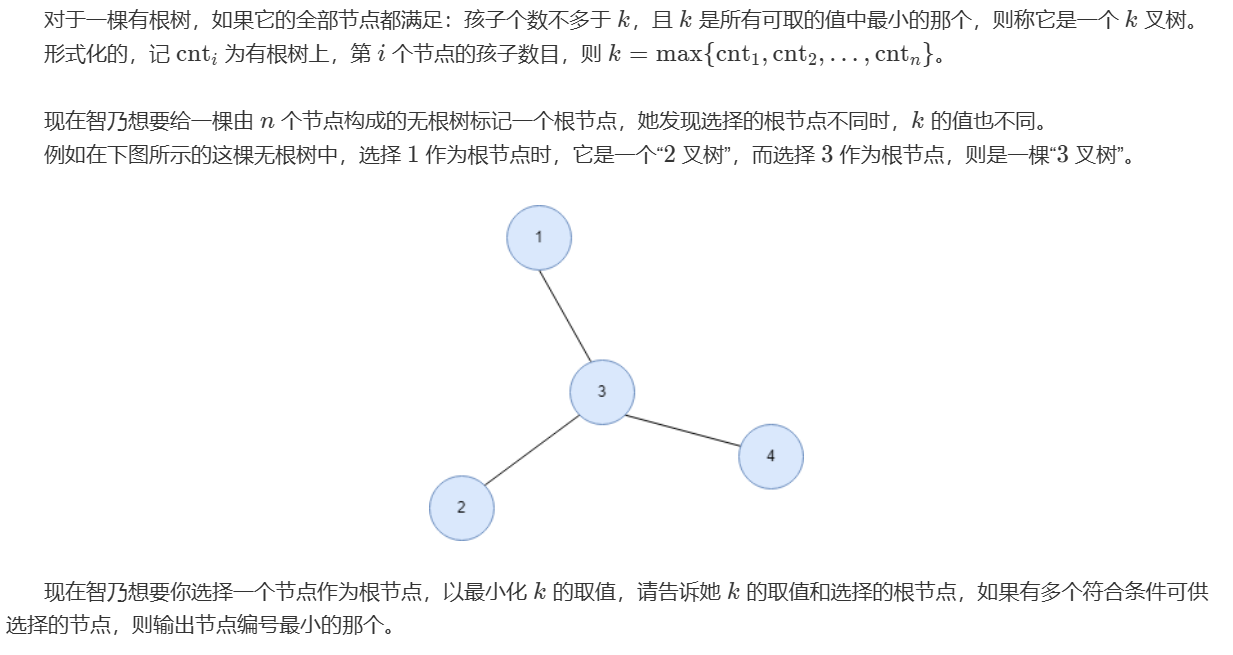
D：

题目大意：

#include<bits/stdc++.h>
#define cintie ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Trd int T;cin>>T;while (T--)solve();
#define LLinf 9e18
#define Iinf 2e9
#define LL long long
#define ULL unsigned long long 

using namespace std;

int n;
vector<int> e[100010];
int dg[100010];
bool st[100010];

void solve(){
	cin>>n;
	if (n==2){
		cout<<1<<' '<<1;
		return;
	}
	int mxdig=0;
	for (int i=1;i<=n-1;i++){
		int u,v;
		cin>>u>>v;
		e[u].push_back(v);
		e[v].push_back(u);
		dg[u]++;
		dg[v]++;
		mxdig=max(mxdig,max(dg[u],dg[v]));
	}
	for (int i=1;i<=n;i++){
		if (dg[i]!=mxdig){
			cout<<mxdig-1<<' '<<i;
            return;
        }
    }
}

int main()
{
	cintie;
	solve();
	
	
	return 0;
}

统计每个点的度数，如果选择一个点为根节点，那么它的叉数为 \(dg[root]\) ，如果一个点 \(i\) 不为根节点，那么它的叉数为 \(dg[i]-1\)

可以统计树中节点的最大度数，因为要使这棵树的叉数最少，那么选有最大度数的节点为根节点一定是劣的

又因为需要找出一个编号最小的节点为根节点，所以从小到大枚举每个节点，只要这个点不是有最大度数的节点，那么答案一定优

特别的，对于 \(1,2\) 两个节点构成的树需要特判