题目描述

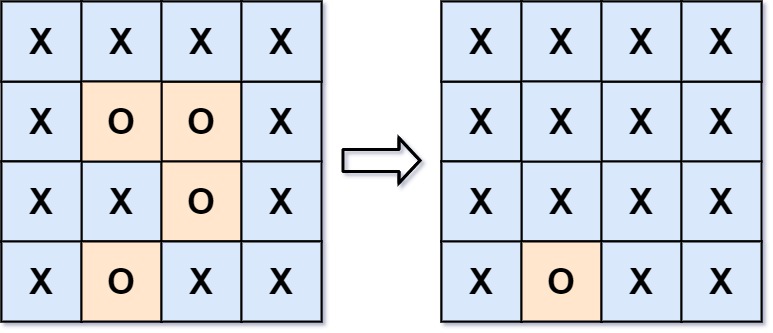
给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。
​

示例 1：
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。


示例 2：

输入：board = [["X"]]
输出：[["X"]]

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/surrounded-regions

解题思路

必须是完全被围的O才能被换成X，也就是说边角上的O一定不会被围，进一步，与边角上的O相连的O也不会被X围四面，也不会被替换。

这个问题也可以用 Union-Find 算法解决，虽然实现复杂一些，甚至效率也略低，但这是使用 Union-Find 算法的通用思想，值得一学。

你可以把那些不需要被替换的O看成一个拥有独门绝技的门派，它们有一个共同祖师爷叫dummy，这些O和dummy互相连通，而那些需要被替换的O与dummy不连通。

首先要解决的是，根据我们的实现，Union-Find 底层用的是一维数组，构造函数需要传入这个数组的大小，而题目给的是一个二维棋盘。

这个很简单，二维坐标(x,y)可以转换成x * n + y这个数（m是棋盘的行数，n是棋盘的列数）。敲黑板，这是将二维坐标映射到一维的常用技巧。

其次，我们之前描述的「祖师爷」是虚构的，需要给他老人家留个位置。索引[0.. m*n-1]都是棋盘内坐标的一维映射，那就让这个虚拟的dummy节点占据索引m*n好了。

思路参考：https://labuladong.gitbook.io/algo/shu-ju-jie-gou-xi-lie/shou-ba-shou-she-ji-shu-ju-jie-gou/unionfind-suan-fa-ying-yong

解题代码

class Solution {
    public void solve(char[][] board) {
        if (board.length == 0) {
            return;
        }
        int m = board.length;
        int n = board[0].length;
        // 给dummy留一个额外的位置
        UnionFind uf = new UnionFind(m * n + 1);
        int dummy = m * n;
        // 将首列和末列的O与dummy连通
        for (int i = 0; i < m; i++) {
            if (board[i][0] == 'O') {
                uf.union(i * n, dummy);
            }
            if (board[i][n - 1] == 'O') {
                uf.union(i * n + n -1, dummy);
            }
        }
        // 将首行和末行的O与dummy连通
        for (int i = 0; i < n; i++) {
            if (board[0][i] == 'O') {
                uf.union(i, dummy);
            }
            if (board[m - 1][i] == 'O') {
                uf.union(n * (m - 1) + i, dummy);
            }
        }
        // 建立方向数组，上下左右搜索常用方法
        int[][] d = new int[][]{{1,0}, {0,1}, {0,-1}, {-1,0}};
        for (int i = 1; i < m - 1; i++) {
            for (int j = 1; j < n - 1; j++) {
                if (board[i][j] == 'O') {
                    // 将当前位置的O与上下左右的O连通
                    for (int k = 0; k < 4; k++) {
                        int x = i + d[k][0];
                        int y = j + d[k][1];
                        if (board[x][y] == 'O') {
                            uf.union(x * n + y, i * n + j);
                        }
                    }
                }
            }
        }
        // 将不和dummy连通的O都替换为X
        for (int i = 1; i < m - 1; i++) {
            for (int j = 1; j < n - 1; j++) {
                if (!uf.connected(i * n + j, dummy)) {
                    board[i][j] = 'X';
                }
            }
        }
    }

}
/**
 * Union-Find 并查集算法
 */
public class UnionFind {
    /**
     * 连通分量个数
     */
    private int count;
    /**
     * 存储一个棵树
     */
    private int[] parent;
    /**
     * 记录树的重量
     */
    private int[] size;

    /**
     * 构造函数
     * @param n
     */
    public UnionFind(int n) {
        this.count = n;
        this.parent = new int[n];
        this.size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }

    /**
     * 连通两个元素
     * @param p
     * @param q
     */
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) {
            return;
        }

        // 小树接到大树下，较平衡
        if (size[rootP] > size[rootQ]) {
            parent[rootQ] = rootP;
            size[rootP] += size[rootQ];
        } else {
            parent[rootP] = rootQ;
            size[rootQ] += size[rootP];
        }
        count--;
    }

    /**
     * 判断两个元素是否连通
     * @param p
     * @param q
     * @return
     */
    public boolean connected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        return rootP == rootQ;
    }

    /**
     * 查找元素的根结点
     * @param x
     * @return
     */
    public int find(int x) {
        while (parent[x] != x) {
            // 进行路经压缩
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }

    /**
     * 连通分量个数
     * @return
     */
    public int count() {
        return count;
    }
    
}