一点壮压总结 来源题单：https://www.luogu.com.cn/training/3121
壮压DP
1.炮兵阵地
#include <bits/stdc++.h>
using namespace std;
vector<int>st;
int dp[1025][1025];
int f[1025][1025];
int num[1025];
char ch[105][15];
int cal(int x){
if(x==0) return 0;
if(num[x]!=0) return num[x];
int ans=0;
while(x>0){
ans+=(x&1);
x>>=1;
}
return num[x]=ans;
}
int ans=0;
int n,m;
bool check1(int x,int st){//第x行 状态是st;
int y=m;
while(st>0){
int now=st&1; st>>=1;
if(now==1 && ch[x][y]=='H') return 0;
y--;
}
return 1;
}
bool check2(int x,int y){
if(x&y) return 0;
return 1;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>ch[i][j];
}
}
for(int i=0;i<(1<<m);i++){
if( (i & (i<<1))!=0) continue;
if( (i & (i<<2))!=0) continue;
if( (i & (i>>1))!=0) continue;
if( (i & (i>>2))!=0) continue;
st.push_back(i);
}
memset(dp,0,sizeof(dp));
memset(f,0,sizeof(dp));
for(auto v:st){
if(check1(1,v)==1) dp[3][v]=cal(v);
}
if(n==1) for(auto v:st) ans=max(ans,dp[3][v]);
for(auto v:st){
if(check1(1,v)==0) continue;
for(auto u:st){
if(check1(2,u)==0) continue;
if(check2(v,u)==1){
dp[v][u]=dp[3][v]+cal(u);
}
}
}
if(n==2) for(auto v:st){
for(auto u:st){
ans=max(ans,dp[v][u]);
}
}
for(int i=3;i<=n;i++){
memset(f,0,sizeof(f));
for(auto v:st){
if(check1(i-2,v)==0) continue;
for(auto u:st){
if(check1(i-1,u)==0) continue;
if(check2(v,u)==0) continue;
for(auto w:st){
if(check1(i,w)==0) continue;
if(check2(v,w)==0) continue;
if(check2(w,u)==0) continue;
f[u][w]=max(f[u][w],dp[v][u]+cal(w));
}
}
}
memcpy(dp,f,sizeof(dp));
}
for(auto v:st){
for(auto u:st){
ans=max(ans,f[v][u]);
}
}
cout<<ans<<"\n";
return 0;
}
\(dp[x][i][j]\)表示第x行状态是j，上一行状态是i的时候的方案数。
存储两行就可以了。因为第x行状态是j，上一行状态是i，在转移的时候就可以知道\(dp[x-1][i][j]\)，此时的i相对于x行，过了两行，也就是需要判定可不可以的最上界。
多打一些check函数 有助于 节约时间清晰代码
2. [P3052]
题目：
给出n个物品，体积为w[i]，现把其分成若干组，要求每组总体积<=W，问最小分组。(n<=18)
思路：
2的18次方是\(262144\)。\(n*2^{18}\)是可以过的。
很明显可以有用\(i\)的每一个位来表示状态。
第一层枚举所有状态，第二层枚举每一个新放进去的物品。
简单地说：\(旧状态+枚举转移\) 这两者可以自动推理出来新状态，就更新了。
复杂度\(n*2^{18}\)。
具体转移条件：
- 当要搞进去的新的物品的时候，如果剩下的体积是直接可以放进去的，就直接更新。（更新的意思是可以放，但是可能放进去不是最优秀的，所以是指更新）。
- 如果体积不可以，就直接默认需要新开一组来存放这个物品更新。（更新的解释同上文）。
貌似有些时候是明明不需要直接使用新的组别，是可能可以装进来其他物品的，但是我直接更新了。
为什么没有问题呢？因为现在强制要求要把当前看中的物品装进来。
而且，可以装进来其他物品的情况，在枚举看中的物品的时候，一定可以枚举到这个物品。也就是说最优解只可能晚点出现，但一定会出现。
\(g[i]\)表示状态为i的时候此时最后一组还剩余的最大体积。
最大体积在遍历，枚举转移的过程中，发挥很重要的作用。
代码：
#include <bits/stdc++.h>
using namespace std;
int a[20];
const int N=1<<18;
int f[N],g[N];
int main()
{
// cout<<(1<<18)<<endl;
memset(f,0x7f,sizeof(f));
memset(g,0,sizeof(g));
int n,w;
cin>>n>>w;
for(int i=1;i<=n;i++){
cin>>a[i];
}
sort(a+1,a+1+n);
f[0]=0;
g[0]=0;
for(int i=0;i<(1<<n);i++){
for(int j=1;j<=n;j++){
int pos=1<<(j-1);
if(i&pos) continue;
if(g[i]>=a[j]){
if(f[i|pos]>f[i] || (f[i|pos]==f[i] && g[i|pos]<g[i]-a[j])){
f[i|pos]=f[i];
g[i|pos]=g[i]-a[j];
}
}
else{
if(f[i|pos]>f[i]+1 || (f[i|pos]==f[i]+1 && g[i|pos]<w-a[j])){
f[i|pos]=f[i]+1;
g[i|pos]=w-a[j];
}
}
}
}
cout<<f[(1<<n)-1]<<"\n";
return 0;
}
3.327E - Axis Walking
题意：
有n张卡牌，每一次随便选择一张扔掉，自己的坐标加上对应的数字。
有两个坐标是一定不能到达的。
问：有多少种把卡牌都扔掉的方案数？
思路：
n=24
壮压DP
用\(f[i]\)表示现在状态为i的时候的方案数，用\(dis[i]\)表示状态为i时候的当前距离。
其中状态i，比如5：\(101\)代表的是第一张用了、第二张没有使用、第三张也使用了的情况。
前置知识：lowbit:
return x&(-x) ; 返回数字x在二进制下面的最后一个1的所有右边的数字，包含这个1.
方案数字记录：
for(int i=x;i>0;i^=j){
int j=i&(-i);
f[x]=(f[x]+f[x^j])%mod;
}
上面循环中用位运算枚举了现在的状态：\(x\)的上一个状态的所有情况，加上就可以统计答案。
每一次处理复杂度：\(O(logn)\)
状态转移：
for(int i=1;i<(1<<n);i++){
int j=i&(-i);
dis[i]=dis[i^j]+dis[j];
if(dis[i]==b1 || dis[i]=b2) continue;
cal(i);//统计i的答案。
}
CODE:
#include <bits/stdc++.h>
using namespace std;
int dis[1<<24],f[1<<24];
int a[25];
const int mod=1e9+7;
void cal(int x){
int j;
for(int i=x;i>0;i^=j){
j=i&-i;
f[x]=(f[x]+f[x^j])%mod;
}
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
int b1,b2; b1=b2=-1;
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>dis[1<<i];
}
int m; cin>>m;
if(m>0) cin>>b1;
if(m>1) cin>>b2;
f[0]=1;
for(int i=1;i<=((1<<n)-1);i++){
int j=i&-i;
//返回的是j的最后一个1开始从左往右的所有二进制数字组成的数。
dis[i]=dis[i^j]+dis[j];
if(dis[i]==b1 || dis[i]==b2) continue;
cal(i);
}
cout<<f[(1<<n)-1]<<"\n";
return 0;
}
小结：虽然每一次用的谁是会影响结果的，因为必须统计方案。
但是最后一个是谁 也不是很关键 因为 最后也可以特别的处理方案就行了。
在距离的时候认为一定是当前的最后一个1得来的就可以。
4.P2622 关灯问题II
题意：
给定10个灯，最开始都是开的。
有\(m<=100\)个按钮，每一个按钮对于每一个灯都有对应的效果，分别为1,0，-1.题目里面直接给出效果，效果的具体含义为：
如果\(a_{i,j}\) 为 1，那么当这盏灯开了的时候，把它关上，否则不管；如果为 −1 的话，如果这盏灯是关的，那么把它打开，否则也不管；如果是 0，无论这灯是否开，都不管。
初始所有的灯都是开的，问最少要按动几次按钮才可以最终所有的灯都关闭？
思路：
壮压是很容易可以想到的，因为n只有10个，状态最多也就只有1024种。
用一个数字的二进制代表相应的位置上面现在灯光的开关状态。
考虑一般性的dp，枚举初始状态和操作的开关的种类。时间复杂度总是对不上。
之前的题目有一个共性的特点，如果用二进制表示里面的1代表这个东西是用过的，那么111.一定是由011 或者101 或者110 三者推理过来的。这样会导致从0开始往大的地方遍历是合理的，当前遍历到的点，一定已经把所有这个状态的前驱状态都推理过。
但是此题并没有如此特点，因为按动一次按钮之后所有位置都会发生不可预料的变化。
注意最后需要的是次数，并且状态最多只有1024种，考虑\(bfs\)跑最短路。
\(dis[st]\)表示状态为st，从所有灯都开到这种状态需要的最少次数。
每一个新的状态，枚举所有的开关进行改变，更新出新状态，压入队列即可。
#include <bits/stdc++.h>
using namespace std;
int n,m;
int w[105][15];
int dis[1<<10];
int main()
{
memset(dis,0x3f,sizeof(dis));
cin>>n>>m;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
cin>>w[i][j];
}
}
int st=(1<<n)-1;
dis[st]=0;
queue<int>q;
q.push(st);
while(!q.empty()){
int t=q.front();
q.pop();
for(int i=1;i<=m;i++){
int st2=0;
for(int j=1;j<=n;j++){
int mo=(t>>(j-1))&1;
if(w[i][j]==1) mo=0;
if(w[i][j]==-1) mo=1;
st2|=(mo<<(j-1));
}
if(dis[st2]>dis[t]+1){
dis[st2]=dis[t]+1;
q.push(st2);
}
}
}
if(dis[0]>1e8){ cout<<"-1\n";}
else cout<<dis[0]<<"\n";
return 0;
}
5.[P7098 凉凉
题意：
每一个地铁站在对应的深度开放站口的时候都会有一定的花费。
一个地铁线路是一个深度，但是如果两条地铁线路有重复的站点就不能在同一深度。
问合理安排之后，仅仅考虑建设地铁站的花费的最小值是多少？
代码：
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=25;
const int M=1e5+6;
const int INF=1e17;
int n,m;
int dep[N][M];//深度为n的时候m种东西的花费。
int cnt[N],sub[N][M];
int cost[N][N];//cost[i][j] 表示线路i在深度j的时候的花费。
int f[N][200005];
int vis[N][N];//标记两个站能不能一起用？
int g[N][200005];
signed main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>dep[i][j];
}
}
for(int i=1;i<=n;i++){
cin>>cnt[i];
for(int j=1;j<=cnt[i];j++){
cin>>sub[i][j];
for(int k=1;k<=n;k++){
cost[i][k]+=dep[k][sub[i][j]];
}
}
sort(sub[i]+1,sub[i]+1+cnt[i]);
}
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
vis[i][j]=vis[j][i]=1;
int x=1; int y=1;
while(x<=cnt[i] && y<=cnt[j]){
if(sub[i][x] == sub[j][y]){
vis[i][j]=vis[j][i]=0; break;
}
if(sub[i][x] < sub[j][y]){
x++;
}
else y++;
}
}
}
int stk[25];
for(int s=0;s<(1<<n);s++){
int top=0;
int st=s;
bool flag=0;
for(int j=1;j<=n && st>0;j++){
if(flag) break;
if(st&1){
stk[++top]=j;
for(int k=1;k<top;k++){
if(vis[j][stk[k]]==0){
for(int z=1;z<=n;z++)
g[z][s]=INF;
flag=1; break;
}
}
for(int k=1;k<=n;k++){
g[k][s]+=cost[j][k];
}
}
st>>=1;
}
}
for(int s=1;s<(1<<n);s++){
f[1][s]=g[1][s];
}
for(int i=2;i<=n;i++){
for(int S=0;S<(1<<n);S++){
f[i][S]=f[i-1][S];
for(int s=S;s;s=(s-1)&S){
f[i][S]=min(f[i][S],f[i-1][s^S]+g[i][s]);
}
}
}
cout<<f[n][(1<<n)-1]<<"\n";
return 0;
}
6.[宝藏]([NOIP2017 提高组] 宝藏)
题意：（题目本身没有看懂）
有n个点，\(n<=12\).
在一个有n个点组成的地图里面挖路。
最开始可以任意选择一个点作为起点不需要任何花费直接到达，并在此基础上再地图上面进行扩展。
目的是把n个点变得连通起来。
如果：接下来选择了从\(a->b\)这条路要挖通.
前提条件：存在一条已经挖好的道路从起点到达a。
花费：挖当前道路的花费为：从起点到a的路径上面经过的点的个数 (包括起点和结点a)\(num\)
花费为：\(num*len_{新挖的路}\)
问最小花费把所有点都挖通。
思路：
本身想要模仿上面的题目，但是发现，如果定义dp数组为前i个点的某种状态下的花费，因为点的位置是随机的，并不是一排排好的，用上面的数组，在注意上有很大的问题。
可以发现我们最终的结果一定是一颗树的形式。并且根就是我们选择的起点。
考虑图模型：
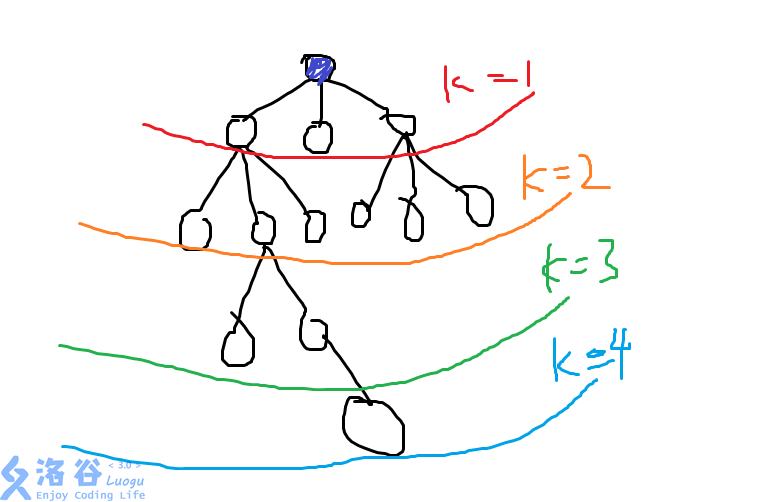
图上的k是层数的意思。很明显越往上（越靠近起点，k越小）。引发思考之前数组里面的i，现在不用来表示编号的前i个，用来表示层数的前i层里面，最后地图挖通的状态下的最小花费。
\(dp[2][5]\)就表示在前两层里面，把点1和点3都挖通了之后的最小花费。（因为5的二进制表示就是第一位和第三位为1。）
这样就可以得到转移方程：
for(int i=2;i<=n;i++){
for(int S=0;S<(1<<n);S++){
for(int s=S;s;s=(s-1)&S){
f[i][S]=min(f[i][S],f[i-1][s]+(从前i-1层的s状态到达第i层的S状态的花费));
}
}
}
接下来只需要预处理出来上面程序中的：从前i-1层的s状态到达第i层的S状态的花费即可。
如果限定了一定是从i-1层到的第i层，那么只需要知道从s->S 新增的路径长度再乘上 (i-1)即可。
对于从s->S的过程：
定义tmp=s^S;
tmp里面所有为1的位数，就代表这次要新增进来的结点编号。
可以从哪些点新增进来？一定是用 s里面现在拥有的结点中转移过来的。所以遍历一下记录最小的就可以。
#include <bits/stdc++.h>
using namespace std;
const int INF=1e8;
const int N=14;
int dis[13][13];
int tran[1<<12][1<<12];
long long f[13][1<<13];
signed main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) dis[i][j]=INF;
}
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y; cin>>z;
if(dis[x][y]>z) dis[x][y]=dis[y][x]=z;
}
memset(tran,0x3f,sizeof(tran));
for(int i=0;i<(1<<n);i++){
for(int s=i;s;s=(s-1)&i){
tran[s][i]=0;
//s是i的子集 模拟从s推理出来i.
int tmp=s^i;//新增的。
for(int j=1;j<=n;j++){
if(((tmp>>(j-1))&1)==0) continue;
int mina=INF;
for(int o=1;o<=n;o++){
if(((s>>(o-1))&1)==1){
mina=min(mina,dis[o][j]);
}
}
if(mina==INF){
tran[s][i]=INF;
break;
}
else tran[s][i]+=mina;
}
}
}
//经过上面的书写 就把所有的从一个集合转变为另外一个集合的所有状态都搞出来了。
// for(int i=0;i<(1<<n);i++){
// for(int j=0;j<(1<<n);j++){
// cout<<i<<" "<<j<<" "<<tran[i][j]<<endl;
// }
// }
memset(f,0x3f,sizeof(f));
for(int i=1;i<=n;i++){
f[1][1<<(i-1)]=0;
}
for(int i=2;i<=n;i++){
for(int S=0;S<(1<<n);S++){
for(int s=S;s;s=(s-1)&S){
if(tran[s][S]!=INF)
f[i][S]=min(f[i][S],f[i-1][s]+tran[s][S]*(i-1));
}
}
}
long long ans=INF;
for(int i=1;i<=n;i++){
ans=min(ans,f[i][(1<<n)-1]);
}
cout<<ans<<"\n";
return 0;
}
关键在于：状态转移方程从原先的前i个点的一些状态进行转移，转变为前i层的状态进行转移。
预处理以及最后的状态转移都是很好想到的。
总结：
-
炮兵阵地：和互不侵犯差不多，更像是通过状态压缩信息之后进行模拟。
-
[327E - Axis Walking]：典型的1101 是从0101 1001 1100三种状态中的一种转移过来：
典型的每次只会多一个的状态转移。
这样的转移明显范围\([0,2^n]\)。且for循环从0开始逐渐\(++\)即可。
small tips: 拿统计最后得到x的方案举例：void cal(int x){ int j; for(int i=x;i>0;i^=j){ j=i&-i; f[x]=(f[x]+f[x^j])%mod; } } -
P2622 关灯问题II]: 因为每一种操作会对n种物品会产生各自不一定相同的影响，而且n比较小，直接把n种物品的状态压起来用数的二进制表示即可。跑\(bfs\)最短路.
-
P7098 凉凉 和 宝藏：\(dp[i][s]\)表示前i层已经处理的物品信息状态为s的情况下的最小花费。
最后的转移方程，往往都是：for(int i=2;i<=n;i++){ for(int S=0;S<(1<<n);S++){ f[i][S]=f[i-1][S]; for(int s=S;s;s=(s-1)&S){ f[i][S]=min(f[i][S],f[i-1][s^S]+g[i][s]); } } }对于里面的\(g[i][s]\)往往需要预处理出来。
宝藏里面还涉及到了从前i个的转移思想转换为前i层的转移思想。 -
解释一下最常见的一种推理的dp里面出现的公式：
int j; for(int i=x;i;i=i^j){ j=i&(-i); //j代表的是当前x的最后一位的1和右边的东西。 //之后i^j 相当于让i把最后一个1变为0。 //这个过程就可以枚举出来1101 里面的：0001、0100、1000； //也就是所谓的当前状态，是由于原来的状态多了一个1推理出来。 //并且 这个过程 往往是可以通过从0开始往上面递增把所有的情况都遇到的。 //复杂度：logn. }另外一种：
现在的状态是1101，但是每一次操作能够加进去的1都是没有任何限制条件的，因此：
有：0001、0100、1000、1100、0101、1001、1101 7for(int S=0;S<(1<<n);S++){ for(int s=S;s;s=(s-1)&S){ //s就会把所有的 S 的子集搞出来。 f[S]=max(f[S],f[s^S]+g[s]); } }
