[Educational Codeforces Round 118 (Rated for Div. 2)]题解
A
题意:
给定两个数,每一个数有两个属性,第一个属性是p1,第二个属性是p2.表示这个数有p2个后缀0.这个数本身等于p1后面加p2个0.问给你两个这种数,判断大小。
思路:
赛场上想到的:如果最终的长度不一样,可以直接根据长度判断。
如果相等,就把后缀0加上直接比较大小就可以(比较字典序的大小),但是后缀0的个数有1e6个,可能会有问题,可以让两个后缀0都减去公共部分,就节省很多时间。
其他人的思路:
直接把第一个属性赋值为double,然后更改为<=10的数,后缀的0的个数会不断增加。
这样子预处理之后直接比较第二个属性的大小,相等的时候比较第一个属性就可以了。
cin>>x1>>p1>>x2>>p2;
while(x1>10){x1/=10.0;p1++;}
while(x2>10){x2/=10.0;p2++;}
if(p1==p2){
if(x1>x2) cout<<">"<<endl;
if(x1<x2) cout<<"<"<<endl;
if(x1==x2) cout<<"="<<endl;}
else{
if(p1>p2) cout<<">"<<endl;
if(p1<p2) cout<<"<"<<endl;
if(x1==x2) cout<<"="<<endl;}
B
题目:给定一个数组,数组里面有n个不一样的数。输出n/2对的x和y满足:
1》x和y不相等.
2》x和y都在数组里面出现过.
3》x%y在数组里面没有出现过.
思路:
x%y 没有出现过,就必须保证x>y,如果x小,取模结果就是x就是数组里面的元素。
如何保证x%y之后的结果没有出现过? 直接用最小的元素做y就可以了。因为某个元素是可以重复使用的,但是不能出现输出的结果中出现相同的一对。
C
题目:题意有点复杂,大概意思就是最终我要覆盖k个数,现在有n个数,如果你最后使用了i秒,每个数会从自己往外扩展i-1个额外的数,带上自己就是i个数。但是会有重合
如果是1 3, 当k=3的时候1可以覆盖1 2 但是1再覆盖3是一件没有实际收益的事情,因为3在第一次的时候3本身就覆盖了。输出最小的时间使得覆盖区间长度>=k。
思路:
第一种: 二分
bool check(int x){
int ans=0;
for(int i=1;i<=n;i++){
ans+=min(a[i+1]-a[i],x);
}
if(ans>=k) return 1;
return 0;
}
void solve(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>a[i];
}
a[n+1]=0x3f3f3f3f3f3f3f3f;
int l=1;
int r=k;
while(l<r){
int mid=(l+r)>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
cout<<l<<endl;
}
第二种差分操作:
根据每两个数之间的差距构建一个新的数组,然后对这个数组进行一个排序,最后得到k1,k2,k3
在1—k1秒内,每多一秒,就会覆盖区间多n,一旦时间大于了k1,每多一秒,多覆盖的区间数是n-1.一次类推
因为n只有100所以这样是过得去的,而且如果n=5e5可以可以的。
int a[N];
int b[N];
void solve(){
int n,sum;
cin>>n>>sum;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<n;i++){
b[i]=a[i+1]-a[i];
}
sort(b+1,b+n);
for(int i=n-1;i>=1;i--){
b[i]=b[i]-b[i-1];
}
int ans=0;
int tim=0;
int now=n;
bool flag=0;
for(int i=1;i<n;i++){
if(b[i]*now>=sum){
tim+=(sum+now-1)/now;
flag=1;
break;
}
else{
sum-=b[i]*now;
now--;
tim+=b[i];
}
}
if(flag) cout<<tim<<endl;
else cout<<sum+tim<<endl;
}
D
题目:
MEX 的含义就是一个序列里面第一个不存在的非负数。
给定一个数组。问有多少个子序列subsequense,subsequence的长度是k.(不要求连续的那种)满足:
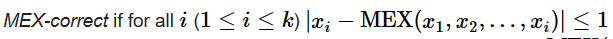
思路:
1900的DP果然目前还是达不到啊。题目里面n有5e5但是保证最大的数不会超过n,所以数的大小就是可以作为dp的下标的。考虑如何状态转移。
对于一个数x,想要加到一个序列的后面(这个过程相当于从前往后进行处理,看看自己能不能加在之前已经有过的后面,如果可以,就dp...+=dp...),那么这个序列的mex就必须是x-1 x+1 x三种情况之一。如果小于x-1,大于x+1都是不行的。
对于一个序列,如果mex是5,有以下两种情况:
情况一:0 0 0 1 1 2 3 4
情况二:0 1 2 3 4 6
第一种是现在这个序列里面不可能拥有大于mex的数,必须以mex-1结尾。第二种情况是里面以mex+1结尾。
这里插一句:如果是0 1 2 3 4 6 1 是不可以的,因为当取最后一个位置的时候xi-mex的绝对值不符合要求。
那么对于一个现在新读入的数,可以有三种mex的序列可能能加进去,每一种mex里面最多有两种情况。
然后再加上这个x之后可能会更改为其他状态,直接找到对应状态+上就看可以。具体如下:
dp[x] [0] 表示现在mex是x的时候并且是第一种情况下的方案数。
dp[x] [1] 表示现在mex是x的时候并且是第二种情况下的方案数。

初始化:
感觉初始化是一件非常重要的事情。
最开始是从考虑最开始的dp[0] [0]是MEX是0,且是第一种情况,说白了就是什么都没有,赋值为1.
最后统计结果的时候不把这种情况算进去。
void solve(){
int n;
cin>>n;
for(int i=0;i<=n;i++){
dp[i][0]=dp[i][1]=0;
}
dp[0][0]=1;
for(int i=1;i<=n;i++){
int x;
cin>>x;
dp[x+1][0]+=(dp[x][0]+dp[x+1][0]);
// dp[x+2][0]+=dp[x][1];//这种情况不对。卡了很久。。
if(x!=0) dp[x-1][1]+=(dp[x-1][0]+dp[x-1][1]);
dp[x+1][1]+=dp[x+1][1];
dp[x+1][0]%=mod; dp[x+2][1]%=mod;
dp[x-1][1]%=mod; dp[x+1][1]%=mod;
}
ll ans=0;
ans+=dp[0][1];
for(int i=1;i<=n;i++){
ans=(ans+dp[i][0]+dp[i][1])%mod;
}
cout<<ans<<endl;
}
E
题目:
有一个地图,里面有一个实验室用‘L’表示,现在有一个机器,可以进行上下左右4种活动,但是因为某些原因,导致它很叛逆,也就是你给他下达往左的命令的时候,他一定不会选择往左,如果除了往左他没有其他的方向可以走,他就会选择原地不动。如果有其他方向可以走,他会在所有可以走的方向里面随机选一个。现在给出我们地图的分布,'L'表示实验室的位置,'.'表示是空地,'#'表示是墙壁。机器有可能在空地的任何一个位置,如果对于某个空地,机器在这上面,我们可以通过某些指令使得机器回到实验室,这个空地在最后输出的时候用‘+’来表示。
样例:
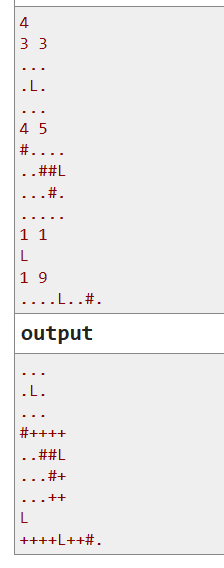
思路:
从L开始进行BFS,把L可以到达的点放进队列,如果这个点上下左右四个方向里面有>=2个位置都是空地,那么目前来看,这个点是不能更改为'+'的,相反就是可以更改的,一旦可以更改就放进队列里面。每次出队的时候,把地图符号直接改为'+'。继续进行判断,直到整个队列为空。
因为有可能,对于某一个点,现在周围有>=2个空地,但是这些空地有可能会变成'+',也就会导致有可能这个空地周围的空地变少。【这个是第一次wa的点,每一个空地,并不是简单的最开始判断一次就可以直接得到其最终的结果】
const int N=1e3+6;
int n,m;
struct node{
int x,y;
};
int dx[]={0,0,-1,1};
int dy[]={1,-1,0,0};
void solve(){
cin>>n>>m;
vector<vector<char> > s(n + 10, vector<char>(m + 10));
vector<vector<bool> > vis(n + 10, vector<bool>(m + 10));
int sx,sy;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>s[i][j];
if(s[i][j]=='L'){
sx=i,sy=j;
}
}
}
queue<node>q;
q.push({sx,sy});
while(!q.empty()){
node tsk=q.front();
vis[tsk.x][tsk.y]=1;
q.pop();
for(int i=0;i<4;i++){
int gx=tsk.x+dx[i];
int gy=tsk.y+dy[i];
if(vis[gx][gy]!=0) continue;
if(s[gx][gy]=='#' || gx<=0 || gx>n || gy<=0 || gy>m) continue;
int flag=0;
for(int j=0;j<4;j++){
int fx=gx+dx[j];
int fy=gy+dy[j];
if(s[fx][fy]=='#' || fx<=0 || fx>n || fy<=0 || fy>m) continue;
flag++;
}
if(flag==2 || flag==1){
if(vis[gx][gy]==0) q.push({gx,gy});
vis[gx][gy]=1;
}
else{
vis[gx][gy]=-1;
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i==sx && j==sy) {
cout<<'L';
continue;
}
if(vis[i][j]==1) cout<<'+';
else cout<<s[i][j];
}
cout<<endl;
}
}
还学习了一下二维的vector的相关操作。[勾八这里真的卡了很久]
vector<vector
vector<vector




