数学学习笔记
学习了基础的数学,发现我的数学还(fei)算(chang)可(la)以(ji),不多说了,开启美妙的数xiao学之旅吧。
插个东西
求和变形(很重要):
- 增加枚举量;
- 交换枚举顺序;
- 分离无关变量;
- 换元法。
进制转换
首先是我们熟悉的进制转换,就是n进制转m进制。
要把n进制数转化十进制数,再把十进制数转化为m进制数。把n进制数转换为十进制数要先模再除,具体过程就不赘述了,把十进制数转换为m进制数其实也差不多,也要先模再除,把一个十进数x拆成m进制数,一个m进制数可以表示成是 \(a0 \times m0+a1\times m1+a2 \times m2+\cdots\)。我们通过 \(x\mod m\) 得到最后一位 \(a\),通过 \(x= x \div m\) 让a1变成最后一位。
给个代码:
while(js)
{
ans[tot++]=js%k;
js/=k;
}
差不多就是这么个东西。
快速幂
进制转换的东西较少较简单,来点稍微有难度的。
其实也不是多难,就是利用二进制思想,判断是否要乘,具体做法就是二进制运算按位与‘1’,然后判断是否要乘,每次操作完,底数的二进制数都要右移一位,进行下次操作。(这个地方强调一下随时取模很重要!)
代码如下:
long long fpow(long long a,long long n)
{
long long ans=1;
while(n)
{
if(n&1)
{
ans=(ans*a)%p;
}
a=(a*a)%p;
n>>=1;
}
return ans%p;
}
这里先补充一个知识点(用处后面肯定有),费马小定理:
有两个互质的整数 a,p,满足 \(a^{p-1} \equiv 1 \pmod{p}\)。
感觉再水就寄寄了!!赶紧来补充一点数学笔记,但是和上边的没有太大关系,今天写的是矩阵快速幂
矩阵快速幂
前置芝士:矩阵乘法
默认大家都会了。
矩阵乘法就是两个矩阵 \(A,B\) 相乘: \(A*B=C\),其中 \(C_{i,j}\) 为 \(A\) 的第 \(i\) 行与 \(B\) 的第 \(j\) 列对应乘积的和,即:
代码大致是这样的:
const int N=100;
int c[N][N];
void mul(int a[][N],int b[][N],int n)//n是矩阵大小,n<N
{
memset(c,0,sizeof c);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++) c[i][j]+=a[i][k]*b[k][j];
好,矩阵快速幂进行了差不多一半了,然后再搞下一半,快速幂。
没错,就真的只是快速幂,把数的快速幂改成矩阵的快速幂就行了。
比如说求矩阵 \(A\) 的快速幂代码可以这样写:
const int N=100;
int c[N][N];
void mul(int a[][N],int b[][N],int n)//n是矩阵大小,n<N
{
memset(c,0,sizeof c);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++) c[i][j]+=a[i][k]*b[k][j];
void Pow(int a[][N],int n)
{
memset(res,0,sizeof res);//n是幂,N是矩阵大小
for(int i=0;i<N;i++) res[i][i]=1;
while(n)
{
if(n&1)
mul(res,a,N);//res=res*a;复制直接在multi里面实现了;
mul(a,a,N);//a=a*a
n>>=1;
}
}
然后再放道题目洛谷P3390 【模板】矩阵快速幂(天哪,博主居然会做题!!)
直接用矩阵快速幂求就好了,注意取模,然后注意数会很大。
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=105,mod=1e9+7;
int read()
{
int x;
scanf("%lld",&x);
return x;
}
struct node
{
int mp[N][N];
};
int k,n;
node mul(node a,node b)
{
node c;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
c.mp[i][j]=0;
for(int k=1;k<=n;++k)
{
c.mp[i][j]+=((a.mp[i][k]%mod)*(b.mp[k][j]%mod))%mod;
}
}
}
return c;
}
node fpow(node mp,int b)
{
node ans,tmp=mp;
for(int i=1;i<=n;++i) ans.mp[i][i]=1;
while(b)
{
if(b&1) ans=mul(ans,tmp);
tmp=mul(tmp,tmp);
b>>=1;
}
return ans;
}
signed main()
{
n=read(),k=read();
node G,res;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
G.mp[i][j]=read();
G.mp[i][j]%=mod;
}
}
res=fpow(G,k);
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
printf("%lld ",res.mp[i][j]%mod);
}
puts("");
}
return 0;
}
别的题???额,不会。
OK又回来补笔记了,说起来得有好长时间没写笔记了。
一道矩阵快速幂的题。
洛谷P4159 迷路
这题一看是 dp 啊,咋会想到矩阵快速幂呢?
(大概是 \(10^9\) 的 t 和 \(10\) 的 n)
先把它当做一道 dp 来做。先考虑若边的长度都等于 1,不妨设 \(f_{i,j}\)为在 i 时刻走到 j 点的路径数,显然 \(f_{0,1}=1\),然后设状态转移,我们发现假设 j 点之前有 1 个与其相连的点 x,那么方案数即为 \(f_{i,j}+f_{i-1,x}\),所以我们可以得到 \(f_{i,j}+=f_{i-1,k}\times z_{k,j}\),其中 \(z_{k,j}\) 表示存在一条 \(k\to j\) 的边。
显然这个 dp 的复杂度是 \(O(n^2 t)\) 的,显然无法通过。我们会发现,在 \(i,j\) 中间加一维数字 1 是不影响结果的,于是式子就变成了 \(f_{i,1,j}+=f_{i-1,1,k} \times z^{k,j}\);然后这个 i 因为是从 1 枚举的,我们假设它为下标,然后就会得到一个 \(f_{i}[1][j]+=f_{i-1}[1][k] \times z[k][j]\)。假设这个 f 和 z 都为矩阵,那很明显 \(f_i+=f_{i-1} \times z\) ,所以最后的 ans 就等于 \(f_{t}[1][n]\)。
第一维 n,第三维 \(n^2\),求一遍 z 矩阵的 t 次幂是 \(\log t\),最终复杂度为 \(O(n^3 \log t)\)。
但是,这题边的长度都不为 1,做法上有一点需要注意的就是把边长不为 1 的边拆成边长条边,每条边的长度就都为 1 了,但是拆多了之后 n 会比较大,复杂度较高,于是我们考虑,对于以下情况:

直接边的话会得到:

对于这种拆边,我们可以把不需要用的点合并在一起,像这样:
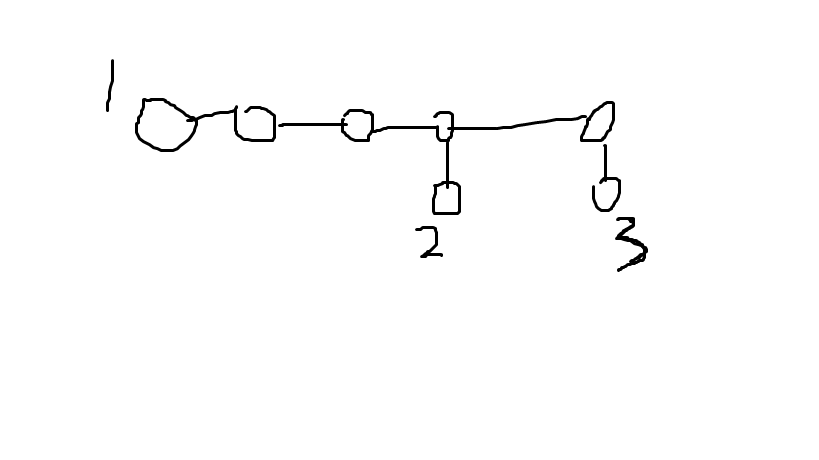
这么操作之后,n 的数量会大大减少,从而降低复杂度。
具体还是看看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read()
{
int x;
scanf("%d",&x);
return x;
}
const int N=105,md=2009;
int n,t;
char s[N];
struct matrix
{
ll v[N][N]; int n,m;
matrix(int r=0,int c=0)
{
n=r,m=c;
memset(v,0,sizeof v);
}
};
inline matrix operator*(matrix x,matrix y)
{
matrix z=matrix(x.n,y.m);
for(int a=1;a<=x.n;++a)
for(int b=1;b<=y.m;++b)
for(int c=1;c<=x.m;++c)
{
z.v[a][b]=(z.v[a][b]+x.v[a][c]*y.v[c][b])%md;
}
return z;
}
inline matrix qpow(matrix x,ll y)
{
matrix res=matrix(x.n,x.m);
for(int i=1;i<=x.n;++i)
res.v[i][i]=1;
while(y)
{
if(y&1)res=res*x;
x=x*x;y>>=1;
}
return res;
}
int main()
{
n=read(),t=read();
matrix h=matrix(9*n,9*n);
for(int i=1;i<=n;++i)
{
scanf("%s",s+1);
for(int j=1;j<=n;++j)
{
if(s[j]=='0') continue;
else h.v[(i-1)*9+s[j]-'0'][(j-1)*9+1]=1;
}
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<=8;++j)
{
h.v[(i-1)*9+j][(i-1)*9+j+1]=1;
}
}
matrix f=matrix(1,n*9); f.v[1][1]=1;
matrix res=f*qpow(h,t);
cout<<res.v[1][(n-1)*9+1]<<"\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号