20199313 2019-2020-2 《网络攻防实践》综合实践
20199313 2019-2020-2 《网络攻防实践》综合实践
本博客属于课程:《网络攻防实践》
本次作业:《第十一周作业》
我在这个课程的目标:掌握知识与技能,增强能力和本领,提高悟性和水平。
1 实验目的
本次实践的目的是复现顶会论文,在实践中掌握新知识,力求站在巨人的肩膀上看世界,提高学生自我素质。通过复现顶会论文来了解论文研究方向、设计思路和运行的具体机制,同时也从这个实验得到相关的经验教训,为今后网络安全相关方面的学习打下基础。
1.1环境配置
1.1.1 Java语言环境
本次实践是在类Java语言的Scala语言环境下进行的实验,因此需要对Java进行良好的配置。
请务必使用成套的Jre(指Java运行环境,简称JRE)和Jdk(JDK是 Java 语言的软件开发工具包,请使用1.6以上版本),我是用的Java 8套件(版本号为1.8.0),后来测试Java14套件也完全可以,如果Jre和Jdk不配套则会极其麻烦,后续实验过程中会报各种错误,既影响心情,又耽误进度。所以前期的繁琐事情务必放在心上,耐心一步一步确保实现到位,每一个环节成功实现功能了再进行下一个环节。
Java语言环境安装包可以从Java官网上免费获取,注意需要成套的相同版本Jre和Jdk。(安装配置教程:https://jingyan.baidu.com/article/624e74597753b734e8ba5acb.html)
1.1.2 Scala语言环境和Sbt运行环境
本次实践是在类Java语言的Scala语言环境下进行的实验,因此需要对Scala进行良好的配置。推荐去官网下载scala-2.12.3+(推荐scala-2.12.3,和作者使用相同版本的Scala-2.12.3 liberary会减少发生错误的概率)。
安装Scala语言同样需要安装Scala语言的运行环境sbt。适用版本为sbt1.0.1+,下载源同样可在Scala官网找到。
以上步骤都是我在Windows操作系统下进行的环境配置,由于本次实验既可以在Windows操作系统下运行也可以在Linux操作系统下进行,所以这里另附Linux操作系统下的配置方法。但是,无论使用哪个系统都得妥善配置环境变量。以上的linux安装均可参考 scala官网--学习--linux安装--运行中步骤进行,这里不再赘述。
1.2 Scala语言
Scala是一门多范式的编程语言,一种类似java的编程语言,设计初衷是实现可伸缩的语言、并集成面向对象编程和函数式编程的各种特性。Scala编程语言抓住了很多开发者的眼球。如果你粗略浏览Scala的网站,你会觉得Scala是一种纯粹的面向对象编程语言,而又无缝地结合了命令式编程和函数式编程风格。Christopher Diggins认为:
不太久之前编程语言还可以毫无疑意地归类成“命令式”或者“函数式”或者“面向对象”。Scala代表了一个新的语言品种,它抹平了这些人为划分的界限。
根据David Rupp在博客中的说法,Scala可能是下一代Java。这么高的评价让人不禁想看看它到底是什么东西。
Scala有几项关键特性表明了它的面向对象的本质。例如,Scala中的每个值都是一个对象,包括基本数据类型(即布尔值、数字等)在内,连函数也是对象。另外,类可以被子类化,而且Scala还提供了基于mixin的组合(mixin-based composition)。
与只支持单继承的语言相比,Scala具有更广泛意义上的类重用。Scala允许定义新类的时候重用“一个类中新增的成员定义(即相较于其父类的差异之处)”。Scala称之为mixin类组合。
Scala还包含了若干函数式语言的关键概念,包括高阶函数(Higher-Order Function)、局部套用(Currying)、嵌套函数(Nested Function)、序列解读(Sequence Comprehensions)等等。
Scala是静态类型的,这就允许它提供泛型类、内部类、甚至多态方法(Polymorphic Method)。另外值得一提的是,Scala被特意设计成能够与Java和.NET互操作。Scala当前版本还不能在.NET上运行(虽然上一版可以-_-b),但按照计划将来可以在.NET上运行。
Scala可以与Java互操作。它用scalac这个编译器把源文件编译成Java的class文件(即在JVM上运行的字节码)。你可以从Scala中调用所有的Java类库,也同样可以从Java应用程序中调用Scala的代码。用David Rupp的话来说,
它也可以访问现存的数之不尽的Java类库,这让(潜在地)迁移到Scala更加容易。
2 实验原理
2.1 时间复杂性
算法复杂度分为时间复杂度和空间复杂度。其作用: 时间复杂度是指执行算法所需要的计算工作量;而空间复杂度是指执行这个算法所需要的内存空间。(算法的复杂性体运行该算法时的计算机所需资源的多少上,计算机资源最重要的是时间和空间(即寄存器)资源,因此复杂度分为时间和空间复杂度。)
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
为了计算时间复杂度,我们通常会估计算法的操作单元数量,每个单元运行的时间都是相同的。因此,总运行时间和算法的操作单元数量最多相差一个常量系数。
相同大小的不同输入值仍可能造成算法的运行时间不同,因此我们通常使用算法的最坏情况复杂度,记为T(n),定义为任何大小的输入n所需的最大运行时间。另一种较少使用的方法是平均情况复杂度,通常有特别指定才会使用。时间复杂度可以用函数T(n) 的自然特性加以分类,举例来说,有着T(n) =O(n) 的算法被称作“线性时间算法”;而T(n) =O(M^n) 和M= O(T(n)) ,其中M≥n> 1 的算法被称作“指数时间算法”。
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f (n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
在各种不同算法中,若算法中语句执行次数为一个常数,则时间复杂度为O(1),另外,在时间频度不相同时,时间复杂度有可能相同,如T(n)=n2+3n+4与T(n)=4n2+2n+1它们的频度不同,但时间复杂度相同,都为O(n2)。
时间频度
一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试,只需知道哪个算法花费的时间多,哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
2.2 最坏时间复杂度
对于一个算法而言最坏时间复杂度的形式可以是很多样的,它可以为常数时间、对数时间、幂对数时间、次线性时间、线性时间、线性对数时间、多项式时间、超越多项式时间、准多项式时间、指数时间等。
若对于一个算法,时间复杂度T(n)的上界与输入大小无关,则称其具有常数时间,记作O(1)时间。若算法的T(n) =O(logn),则称其具有对数时间。由于计算机使用二进制的记数系统,对数常常以2为底(即log2n,有时写作lgn)。若一个算法时间复杂度T(n) = O(nlog n),则称这个算法具有线性对数时间。因此,从其表达式我们也可以看到,线性对数时间增长得比线性时间要快,但是对于任何含有n,且n的幂指数大于1的多项式时间来说,线性对数时间却增长得慢。若T(n) 是以n的指数形式为上界,其中 poly(n) 是n的多项式,则算法被称为指数时间。更正规的讲法是:若T(n) 对某些常量k是由 O(2) 所界定,则算法被称为指数时间。常见各类型的时间复杂度如图1所示.
表一中所展示的则为各种常用排序算法的时间复杂度对应情况。

图1 时间复杂度类型

表1 各排序算法时间复杂度对应表
2.3 寻找最坏时间复杂度的必要性
对于一个正常的算法而言,它有它自己所期望的时间复杂度范围,对于给定输入尺寸的用户输入一般不会比算法设计这预计虽坏情况更糟糕,但是如果我们所找到的最坏情况下的输入比设计者给的范围更糟糕,很有可能会导致一些设计者预料之外的漏洞的产生。
举例说明,若服务器给定的算法预计复杂度情况如下图图2所示,若算法存
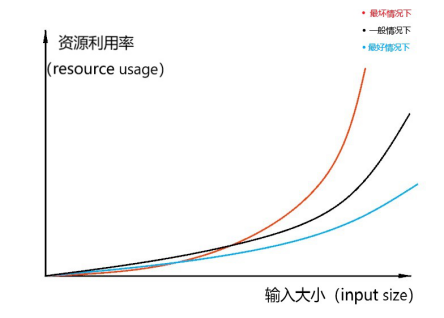
图2 预计算法复杂度

图3 预料之外的算法复杂度
在未知漏洞,使得在特定输入模式下所达到的时间复杂度超出管理员预期,则会出现如图2所示的情况,在通向尺寸的输入大小下,特定输入模式可以占有利用的系统资源量为一般预计情况下最坏的两倍。若输入大小范围规定不当,可以造成的影响则可能会极为糟糕。
我们为了避免这种情况的发生,对于每一种既定的算法,找出算法最坏情况下的输入模式是极为重要的。
2.4 触发目标程序的最坏情况下性能运转的输入
触发目标程序的最坏情况下性能运转的输入(以后简称WPIs)可用于调试性能问题并确认安全漏洞是否存在。部分性能漏洞可用于Ddos攻击,例如刚刚我们举例中提到的占据超额度的系统资源的情况,很容易被用来做拒绝服务攻击。
此外,WPIs可以揭示致使最坏的资源调配运转的原因, 并帮助程序员编写合适的方法来改善这种输入模式下的资源调配,以防止他们的代码受到潜在的威胁或DoS攻击。
2.5 递归运算图
原文中提到的递归运算图(我更形象的称之为递归运算表达式,一下简称RCG)指的是一种描述输入模式或递归模式的运算式或运算图。
RCG的一般形式如图所示, P为表达式,C为常量(Seed或初始化表达式),F为递归算式(也被称为更新表达式), Y为输出表达式,这里由于Y表达式的存在,可以将内部状,态转换为参数输出,有效解决了内部状态数,量与目标算法参数数量不一致的问题。

图4 RCG表达式

图5 RCG运算图
通过RCG我们可以很好的描述一个输入模式是如何进行迭代的,换句话说,阐明了我们通过何种输入模式可以让我们的输入可以在相同的输入大小增速下,更快的占据更多的系统资源。
我们介绍了递归计算图(RCGS)作为表示生成器的DSL 家族。 直观地说,我们选择RCG作为我们的计算模型,因为它们具有足够的表现力来捕捉实践中出现的大多数感兴趣的输入模式,但它们也具有足够的限制性,以使搜索空间易于管理。
2.6 遗传规划算法
遗传规划算法(遗传算法的一个分支,简称GP),是进化算法的一个分支。进化计算包括遗传算法、遗传规划、进化策略和进化规划四种典型方法。第一类方法比较成熟,现已广泛应用,进化策略和进化规划在科研和实际问题中的应用也越来越广泛。
遗传算法的起源可追溯到20世纪60年代初期。1967年,美国密歇根大学J. Holland教授的学生 Bagley在他的博士论文中首次提出了遗传算法这一术语,并讨论了遗传算法在博弈中的应用,但早期研究缺乏带有指导性的理论和计算工具的开拓。1975年, J. Holland等提出了对遗传算法理论研究极为重要的模式理论,出版了专著《自然系统和人工系统的适配》,在书中系统阐述了遗传算法的基本理论和方法,推动了遗传算法的发展。20世纪80年代后,遗传算法进入兴盛发展时期,被广泛应用于自动控制、生产计划、图像处理、机器人等研究领域。
遗传算法的基本运算过程如下:
1、初始化:设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始群体P(0)。
2、个体评价:计算群体P(t)中各个个体的适应度。
3、选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。
4、交叉运算:将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。
5、变异运算:将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。
6、终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
遗传操作包括以下三个基本遗传算子:选择、交叉、变异。
1、突变算子:突变算子用于保持从一代到下一代的基因多样性,并防止算法最终局部收敛。 它创建了一个RCG ′,具体来说,我们首先随机选择初始化表达式、更新表达式或输出表达式F( ),然后选择抽象语法树(AST)中的一个随机节点n,称为突变点,我们的变异算子用一个随机生成的as T替换了根植于n的子树T(其类型与T相同),如图五所示。
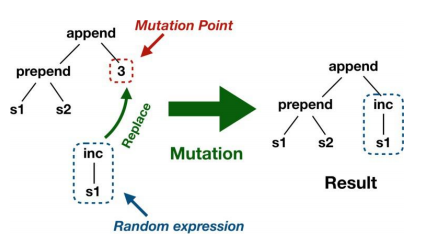
图6 突变算子示意图
2、交叉算子:交叉算子用于将种群中的现有成员组合成新的个体。具体来说,在给定rcg1和G2的情况下,我们从G2中选择了一个τ型突变点n1和另一个τ型突变点n2。然后,我们通过交换根植于n1和n2的子树来创建两个新rcg,并随机选择两个新rcg中的一个,交叉操作如图六所示
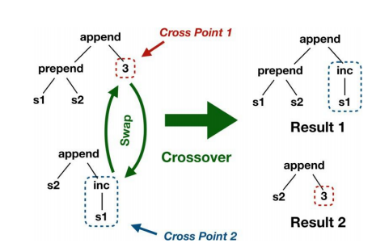
图7 交叉算子示意图
而进化中的适应度则需要评价算法来进行评价。进化论中的适应度,是表示某一个体对环境的适应能力,也表示该个体繁殖后代的能力。遗传算法的适应度函数也叫评价函数,是用来判断群体中的个体的优劣程度的指标,它是根据所求问题的目标函数来进行评估的。由于我们的目标是找到一个最大化目标程序资源利用率的RCG,我们需要依赖适应度函数,适应度函数的最简单实现只使用测量模型M。然而,作为遗传规划的标准,适应度函数不必与优化目标完全相同。我们设计的适应度函数具有以下三个性质:
1、它应该与测量模型M一致,即当M(G)>M(G′)时,G被认为比G′更适合。
2、它应该通过惩罚AST规模非常大的RCG来防止个体进化为无限大的程序。
3、当两个rcg具有相似的大小和资源使用时,它应该使用Occam的razor原则来选择更简单的rcg。
基于以上这些准则,我们的适应度函数评价函数F就可以帮助我们进行筛选 。
3 实验过程
3.1 控制台启动sbt项目
首先我们来启动sbt项目:
Windows操作系统下呼出cmd命令提示符窗口(Win+r开启运行,然后输入cmd回车即可打开),进入sbt项目文件夹,转移目录的方式和Linux类似,都可以使用“ cd ”命令,但是在windows操作系统下需要先转移盘符,即“e:”转移到e盘(我的项目文件在e盘),然后使用cd命令即可转到文件目录,如图七所示。
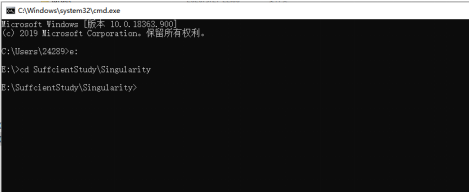
图8 cmd目录切换图1
注意:windows下的cd命令使用的是反斜杠‘\’,而Linux操作系统下使用的是斜杠‘/’。
方法二:直接打开项目文件夹,在地址栏中输入cmd,即可直接切换到当前目录下的命令提示符窗口,如下图图八、图九所示。
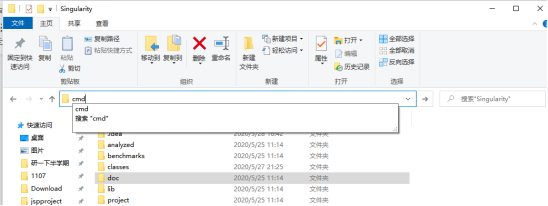
图9 cmd目录切换图2
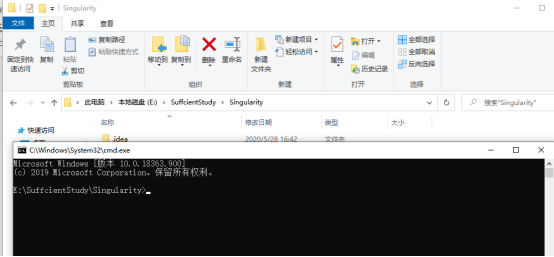
图10 cmd目录切换图3
随后输入sbt run直接运行当前目录下的sbt项目,需要注意,若需成功运行和调试,建议安装IDEA来进行调试,这样会比较方便。
项目这里还有很多问题,例如不能成功输出图片等问题,接下来我带领大家一同修改bug。
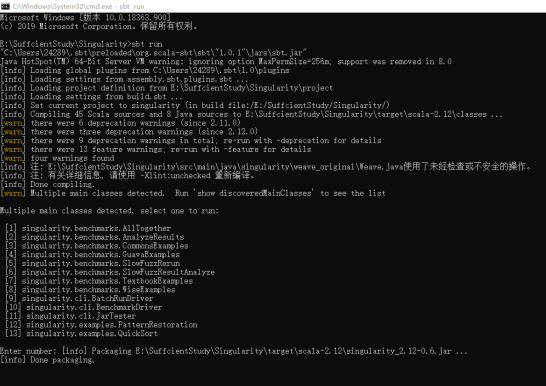
图11 sbt项目运行菜单界面
3.2 修改源代码中的Bug
随后输入sbt run直接运行当前目录下的sbt项目,需要注意,若需成功运行和调试,建议安装IDEA来进行调试,这样会比较方便。
项目这里还有很多问题,例如不能成功输出图片等问题,接下来我带领大家一同修改bug。
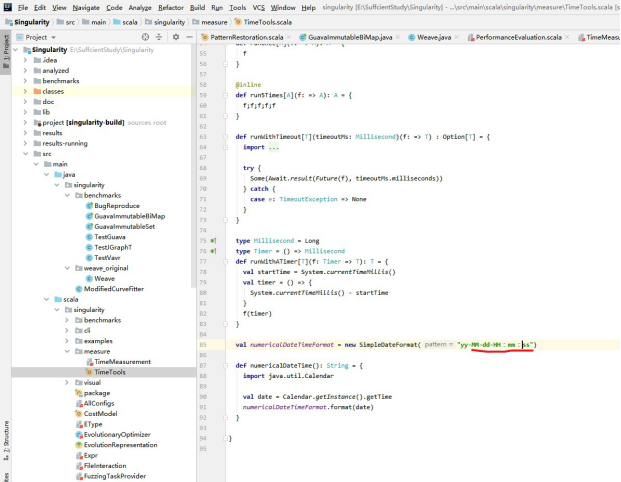
图12 时间工具
由于在国外和国内的文件命名问题(可能国外的命名原则可以使用冒号‘:’,但是国内的文件命名不可以用冒号,所以就会出现图像输出堵塞以及读取不到图像数据和时间戳的问题,这里需要改程中文输入法下的冒号,因为中文输入法下的冒号,在编译时占两字符,视为一个汉字),同理,这个时间工具TiemTools以及TimeMeasurement时间方案中的英文冒号都需要替换为中文。
另外,在图像分析工具中,也应正确修改输出图像的文件名。并且,每一次修改后都应重新加载sbt项目,使修改得到体现,如图十一所示。
图13 图像分析工具
3.3 启动针对快速排序的项目
在3.1节中提到的项目启动方式下,我们可以进入到图10中的菜单选项,接下来我们就可以选择选项13,运行快速排序算法的最坏情况输入的选择了。运行截图如下图12所示:
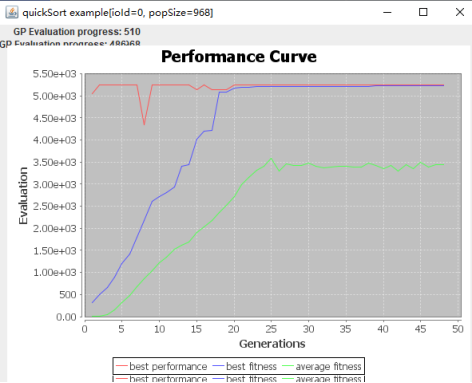
图14 快速排序算法运行图像
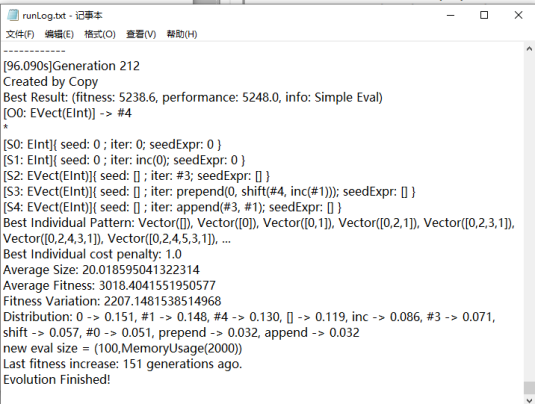
图15 快速排序算法运行日志

图16 快速排序算法最佳RCG
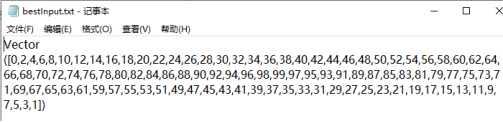
图17 快速排序算法最佳输入数据
我们可以看到在图12中的运行情况,其中红色曲线代表系统资源可分配量,也就是目前检测到的资源分配上限值,即每一代中resourceUsagein 返回的数字ProblemConfig,也就是系统的最佳性能(很显然我们只需要单纯提高输入尺寸就可以达到最大性能,但是这不是我们要关心的地方)。而蓝色曲线则是我们的最坏输入模式的占有资源量,在伴随着每一代的快速迭代和进化,每一代筛选出资源占有量最大的输入模式作为当前代中最差输入,而若超过一百五十代都没有比当前输入模式下的资源占有率更大的输入模式,则认为当前输入模式为最坏情况下的输入模式。绿色曲线则代表每一代中的平均水平的资源占有量,很显然平均水平下的资源占有量较之其他曲线小很多。
在图13中我们可以很清晰的看出每一代的输入模式是如何产生的(变异、交叉等),其中还提到了每一代的输入模式中各部分的贡献因子,这一点要依赖于评价算法(也就是遗传算法的适应度函数)。
输入模式的解读则依赖于图14中描述的RCG(递归运算表达式),输出为式子S4,它反复迭代使用式子S3,同时S1也在更新Seed表达式(自加),由此可以得到一个输入模式,最坏输入只需要通过这个输入模式进行迭代即可得出任意大小的输入。并且这种输入模式是系统占有资源量随迭代次数增加最快的一种输入模式,也就是最坏输入模式(WPI).
3.4 启动针对教科书中十三种算法的分析
在本节中,针对书中提到的17中算法,我进行了最坏时间复杂度测试我们将评奇点算法的适用性,如排序、搜索、图形算法和字符串匹配,这些算法摘自Sedgewick和Wayne的广泛使用的算法教科书。
这个实验的目的是确定奇点是否能够识别这些算法的最坏情况渐近复杂性通过曲线拟合就可以得到输入的时间复杂度情况为了更好地阅读和修改源代码,强烈建议使用Intellij IDEA之类的Scala IDE 。
要运行奇点论文中描述的教科书算法示例集,请在项目根目录中开启命令提示符窗口后键入sbt assembly,sbt项目会启动assembly功能,将所有内容打包到中target/scala-2.12/singularity-assembly-0.6.jar,这一步不可省略(为了产生多个过程,需要额外的包装步骤,默认情况下,将并行运行8个子进程,可以通过设置改变这一数量processNum,但尽管开启了八个子进程同时运算,仍然在我新电脑中以百分之一百cpu占用下运行了三个小时)。
然后键入java -cp target/scala-2.12/singularity-assembly-0.6.jar singularity.benchmarks.TextbookExamples (通常,用于java -cp
该命令会让sbt开始运行奇点论文第7.1节中描述的17个教科书算法示例。所有教科书中的算法代码以及代码和挖掘工具的接口函数、设定都在TextbookExamples.main()文件中。同理,以上运行后的所有结果都将写入results-running和results中。
运行结果如下图16所示,共成功计算了五百多个项目图:

图18 教科书算法运行结果
3.5 利用该发掘工具发现的其他漏洞
3.5.1 JGraphT性能漏洞
流算法(图算法)适用于处理图数据结构的大多数算法,求最短路径等算法(流处理性能缺陷),这里我们利用遗传算法以及找时间复杂度的思路发现了一个性能漏洞。

图19 JGraphT性能曲线
JGraphT中的性能错误。奇点识别了重标号最大流算法JGraft实现中的一个严重性能缺陷。虽然该算法的理论最坏情况是O(n3),但奇点能够找到触发O(n5)运行时间的输入。此模式对应于一个具有2个内部状态和3个输出状态的RCG,如图16所示。使用这些简单但富有表现力的组件,我们能够从JGraphT 的最大流程实现之一中找到复杂性漏洞。我们将找到的输入模式奇点转换为独立的Java代码,并在此bug报告中进行了报告。(https://github.com/jgrapht/jgrapht/issues/461)
我们发现的模式对应于具有2种内部状态的RCG,如下所示:
seed for g: addNode(emptyGraph())
seed for i: 0
updater for i: plus(i,2)
updater for g: growEdge(bridegeEdge(growEdge(g, 3, 0), 4, inc(i), i), 0, 0)
output1 (source index): 2
output2 (sink index): 1
output3 (graph): g
3.5.2 Guava穿孔漏洞
思路同上,结果发现了漏洞,Guava穿孔漏洞,是一种库穿孔漏洞。由于copyOf()函数穿孔,破解了hash防冲突的防撞机制。
哈希码创建的防撞机制(缓解哈希冲突)。算法的穿孔漏洞会导致一些潜在的安全问题,这里以黑盒形式发现了这种输入模式,并且仅将运行时间用作反馈。攻击者可能会使用这种黑盒模糊技术来构造恶意软件攻击。
在我们发现的Guava不可变收集错误中,包含5个内部状态和总共33个AST节点。还要注意,每个整数竞争者的值都可以在0到500之间,因此,除了30个标准分量之外,每个整数值本质上都对应于DSL中的一个新分量,这极大地扩展了总搜索空间,并导致了很多优化问题更具挑战性。这些困难的优化问题只能通过诸如遗传编程的反馈指导技术来有效解决。
type of s0, s1: Int
type of s2, s3: Pair[Int]
type of s4: List[Pair[Int]]
seed for s0: 244
seed for s1: 475
seed for s2: (271, 212)
seed for s3: (239, 26)
seed for s4: []
updater for s0: 170
updater for s1: plus(plus(bitOr(times(times(99, 302), 486), 475), 142), dec(s1))
updater for s2: mkPair(pair2(s2), bitShift(s1, 353))
updater for s3: s2
updater for s4: append(s4,s2)
output: s4
生成的输入要复杂得多且难以理解,但它们利用了Guava哈希涂抹功能的弱点,并触发了n ^ 2的运行时复杂性。由于此错误报告,开发人员在较新版本中更改了其哈希映射实现。
在运行过程中我们可以反复调整出入size变量来拟合出如图17所示曲线。
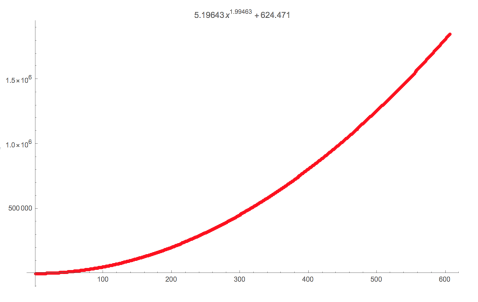
图20 JGraphT性能曲线
生成的输入要复杂得多且难以理解,但它们利用了Guava哈希涂抹功能的弱点,并触发了n ^ 2的运行时复杂性。由于此错误报告,开发人员在较新版本中更改了其哈希映射实现。
4 相关工作的对比
4.1 和Wise算法的对比
WISE是一个基于动态符号执行的白盒测试工具,我们在用于评估Wise的基准上执行这个实验。我们给这两个工具3小时的时间限制,并比较每个基准在由Singularity和Wise生成的输入上的性能。
具体地说,相同训练大小上进行训练,并使用这两个工具为n∈{30,500,1000}生成大小为n的输入。我们使用n=30来匹配原始Wise文件中使用的值。我们还报告了n=500和n=1000,以证明我们的方法比Wise方法的优势。

表2 和Wise在不同尺寸输入下的对比结果
除此之外,由于Wise是一个白盒测试工具,在测试前需要对算法有一个完备的了解,而我们的测试工具是一个黑盒测试工具,相比之下优势显而易见。
4.2 和SlowFuzzing算法的对比
SlowFuzzing是一种最先进的发掘工具,用于寻找可用性的弱点(input not. pattern)这个实验的基准包括SlowFuzz论文中报告的算法,其中包括几个排序算法、PHP的哈希表实现、19个正则表达式匹配问题和bzip2应用程序的zip实用程序。我们在评估中不使用bzip2示例,因为只有在设置了输入文件头中的某些位时才会触发此漏洞;因此,此基准与本文所述的输入模式生成问题无关。
SlowFuzz还能够生成大量的输入,这些输入在现实应用程序中触发不同的算法复杂性漏洞,包括反病毒软件中使用的各种zip解析器、Web应用程序防火墙中使用的正则表达式库以及Web应用程序中使用的哈希表实现。
但是由于SlowFuzzing的穷举特点,它寻找的是特定输入而非我们一直强调的输入模式,其速度是慢于我们的发掘工具的。

图21 和SlowFuzz在不同尺寸输入下的对比结果
5 总结和展望
论文提出了一种新的黑盒漏洞发掘技术,用于生成触发给定程序最坏情况性能的输入。我们方法的基本思想是寻找输入模式而不是具体的输入,并根据最优程序合成来制定复杂性测试问题。 具体来说,使用递归计算图 来表达输入模式,并使用遗传编程来找到一个导致最坏情况行为的 RCG。
实验证明了我们的方法与其他技术相比的优势,并表明我们的方法是有效的 (a)寻找算法的最坏情况下的渐近复杂度的边界,(b)检测非平凡程序中的可用性漏洞,(c)发现广泛使用的Java库中以前未知的性能错误。
这种算法以新颖的思路找到了最坏情况的输入模式,迭代速度远高于单纯寻找输入模式(相对的,也更难评价)算法有效检索了算法(尤其是服务器资源分配上)可能存在的拒绝服务攻击漏洞(性能占比很大的输入会使服务资源很快耗尽)在未来,我们可以尝试利用这种算法为我们的毕设检查漏洞,或者利用其作为一种攻击工具,,或者用这种作为一种服务支撑也很棒。
在这一学期的学习过程中,在王老师亲切的谆谆教导中,在与新冠肺炎的不懈较量中,我们以互联网教学的方式顺利完成了本学期的网络攻防实践的课程。在此期间有诸多困难与不解,王老师都耐心的与我们细细分享他在数十载的钻研中对这门课程以及问题的见解与想法,每每听老师以细致入微的角度进行分析我们的疑惑,我都倍感豁达,开阔了我过去狭隘的眼界,仿佛打开了我新世界的大门,门后是生机盎然的祖国土地,和一套逐渐完备的服务于人民大众的网络安全系统。多年来我国网络空间安全建设取得了巨大的成就,但是仍然存在很多需要解决的问题,仍然有很多方面需要改进。祖国的未来需要年轻人发愤图强,网络攻防实践的学习只是一个开始,未来仍然有许多工作需要我们去努力。最后,感谢王老师这一学期的辛勤教学,未来我们会继续努力!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号