核密度图的绘制
转自:https://www.sohu.com/a/204161532_278730
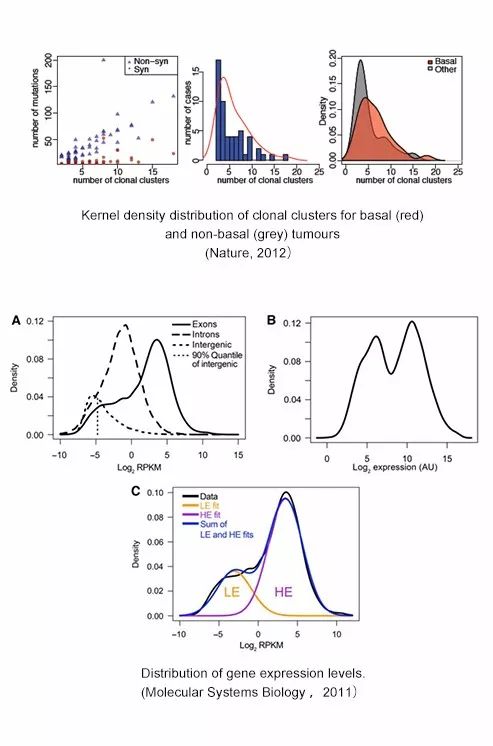
我们先看一下别人家文章中的核密度图。
那么,怎么做出这样的图呢?这种核密度图到底想表达或表现什么呢?
核密度图的绘制
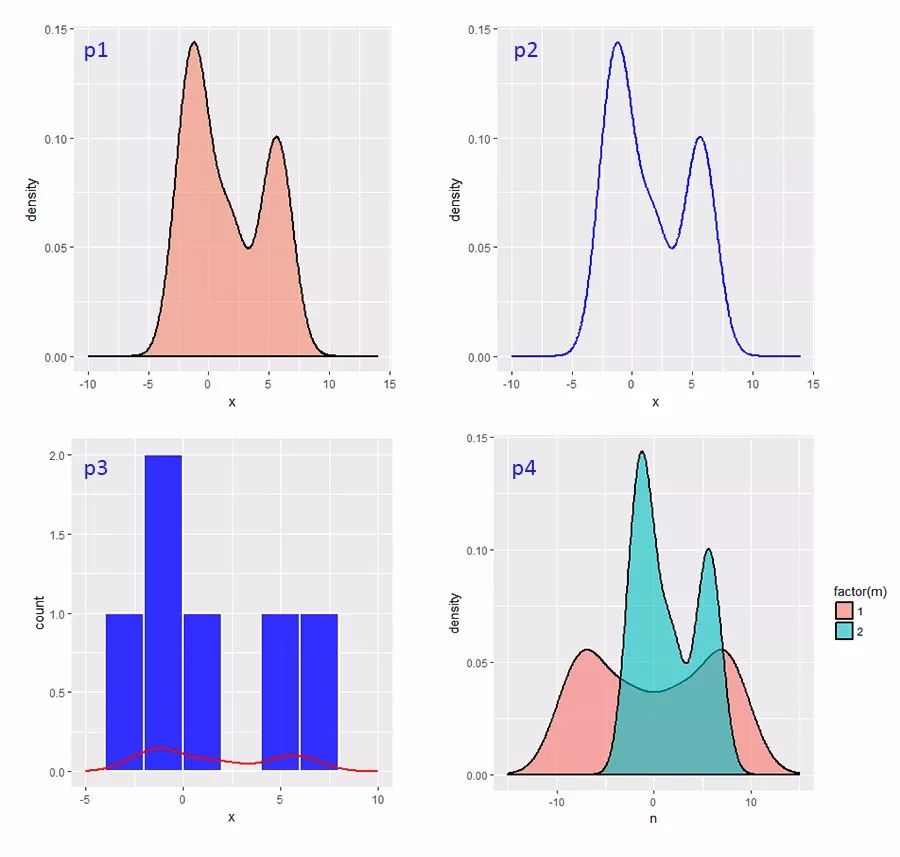
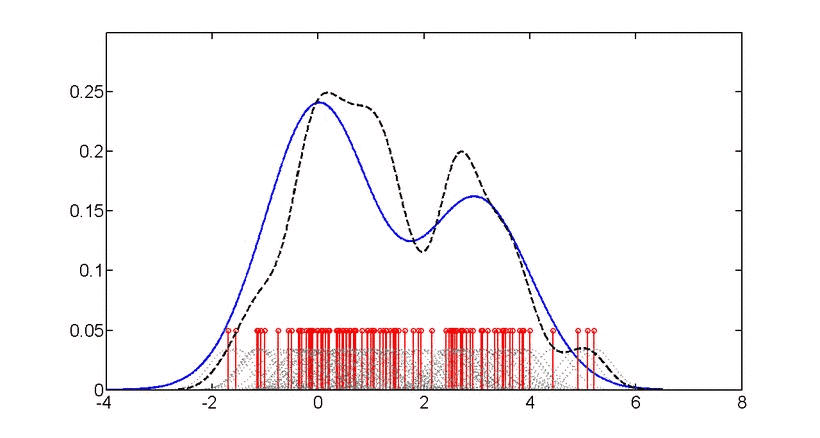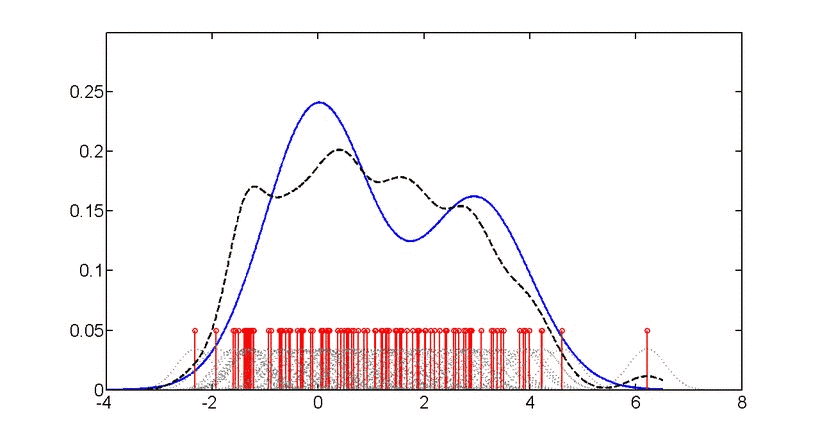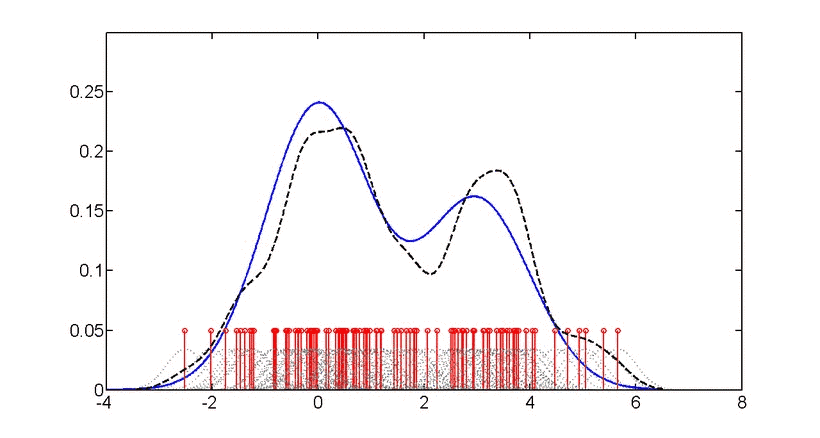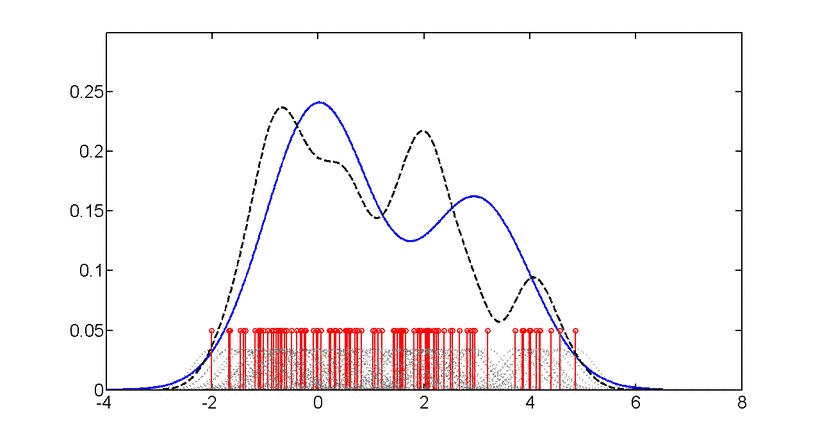
所谓“眼过千遍不如手过一遍”,数据我们这里用Wikipedia文中的这6个数: −2.1, −1.3,−0.4,1.9,5.1,6.2。我们用ggplot2绘制这6个数的核密度图(两种方法,代码对应下图的p1和p2)、直方图和密度图的组合比较(下图p3),与其“镜像翻转”数列“相加”后新数列的密度图(下图p4,橙色)。代码如下:
> library("ggplot2", lib.loc="~/R/win-library/3.4")
> x<-c(-2.1,-1.3,-0.4,1.9,5.1,6.2)
> x
[1] -2.1 -1.3 -0.4 1.9 5.1 6.2
# 载入数据
> p<-ggplot(data=NULL,aes(x=x))
> p1<-p+geom_density(adjust=0.55,fill="#f4876a",colour="black",alpha=0.6,size=1)+xlim(-10,14)
> p1
# 第一种画法,利用geom_density()画的核密度图,“面积”可填充颜色(见下图,p1)。这里的adjust用来调整bw(带宽),数值为默认值的倍数。这里geom_density()默认的核函数为Gaussian,关于带宽的解释见下文。
> p2<-p+geom_line(stat ="density",adjust=0.55,color="blue",size=1)+xlim(-10,14)
> p2
# 第二种画法,方法相类似,最后的结果与p1一致,只是不能填充颜色(下图p2)。
> p3<-p+geom_histogram(binwidth =2,center=1,fill="blue",color="white",alpha=0.8,size=1)
+geom_line(stat ="density",adjust=0.55,color="red",size=1)+xlim(-5,10)
> p3
# 同样的数据,用geom_histogram()画直方图作比较,某种意义上可为bw的调整做参考。
> m<-c(1,1,1,1,1,1,2,2,2,2,2,2)
> z<-c(-8.3,-6.4,-2.3,2.3,6.4,8.3)
> n<-c(z,x)
> data<-data.frame(m,n)
> data
m n
1 1 -8.3
2 1 -6.4
3 1 -2.3
4 1 2.3
5 1 6.4
6 1 8.3
7 2 -2.1
8 2 -1.3
9 2 -0.4
10 2 1.9
11 2 5.1
12 2 6.2
> p1<-ggplot(data=data,aes(x=n,group=factor(m),color=factor(m),fill=factor(m)))
> w1<-w+geom_density(adjust=0.55,alpha=0.6,size=1,colour="black")+xlim(-15,15)
> p4
# 将x这列数据乘以负1,从顺序颠倒后与x相加,生成z,z和x组成数据框,绘制分组核密度图,见p4。本文对图表主题,文字不做调整,调整方法见上一篇文章《ggplot2绘图学习笔记分享》,这里不再赘述。
KDE 简介
核密度估计(kernel density estimation,KDE)是根据已知的一列数据(x1,x2,…xn)估计其密度函数的过程,即寻找这些数的概率分布曲线。我们最常见的密度函数莫过于正态分布(也称高斯分布)的密度函数:
而密度估计就是给定一列数据,分布未知的情况下估计其密度函数。
例如上文的6个数据:c(x1 = −2.1,x2 = −1.3, x3 = −0.4, x4 = 1.9, x5 = 5.1, x6= 6.2),我们看下这列数据的“密度”如何。
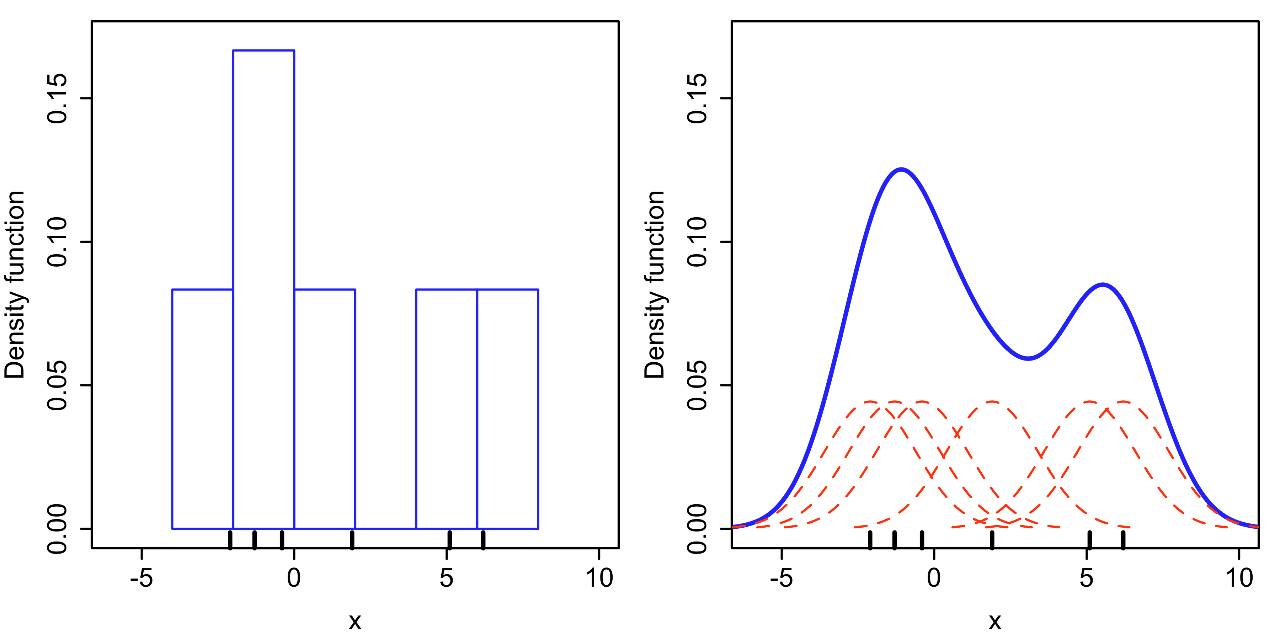
画频率直方图就是一种密度估计的方法(如下图,组距为2),这里的“密度”(density)可以感性得理解为一个区间(直方图的组距)内数据数量的多少,右图即为这6个数据的密度曲线(这里简称为密度图),它是左图的外轮廓化,数据量越多,直方图的顶点也越接近一条线。
https://en.wikipedia.org/wiki/
直方图和密度图都是一组数据在坐标轴上“疏密程度”的可视化,只不过直方图用条形图显示,而密度图使用拟合后的(平滑)的曲线显示,“峰”越高,表示此处数据越“密集”。“密度”越高,如下图。
https://en.wikipedia.org/wiki/
“核”与“带宽”
核密度估计是用用下面的函数去估计一个分部未知的独立样本的分布:
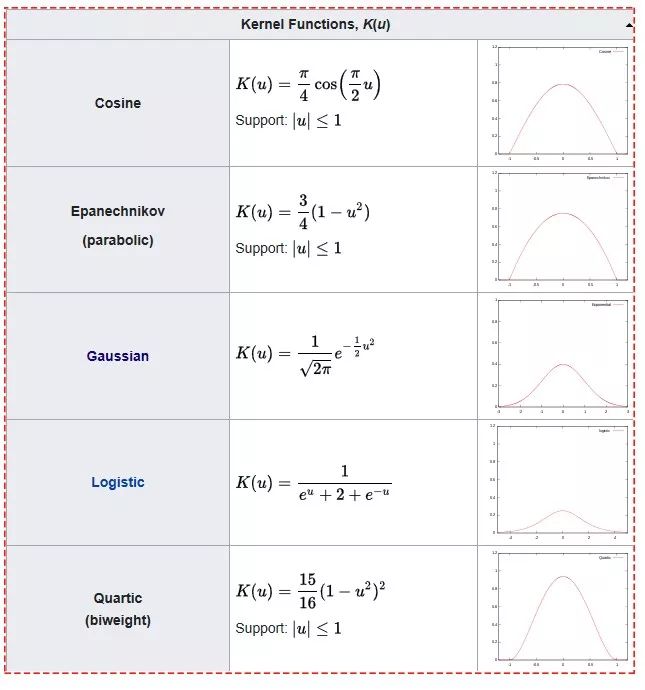
其中K,也就是“核”(kernel)表示核函数,部分常见的核函数如下图(看到Gaussian的函数是不是觉得很眼熟?另为,R中的kernel 有"gaussian","epanechnikov","rectangular","triangular","biweight","cosine","optcosine")。
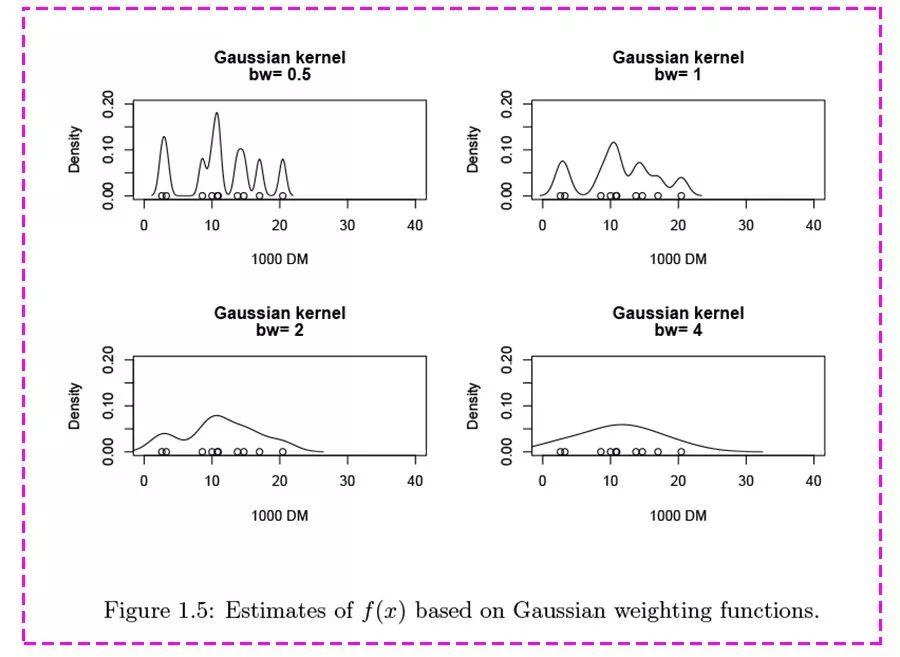
公式里的“h”,被称为“带宽” (bandwidth,也写作bw),为平滑参数,可简单理解为直方图的“组距”,带宽越大曲线越平滑,见下图。
小结
核密度估计实际上是表现一组数据的分布情况,转录组中用来展示所有样本基因的表达量丰度分布,将FPKM取对数后替换本文第1部分绘图的数据,即可画出样本中所有基因表达量的分布图。一般情况下,它可用来比较某个样本跟其它样本间的差异。
当然,也可以用于其他的数据分布的分析,除了箱型图,还可考虑核密度图。
想学ggplot2作图的童鞋可以点击“阅读原文”到在线课堂看周老师的视频教程,每个视频都可下载课件和数据。今天的就到这里啦,若觉得本文还不错要记得分享哦~

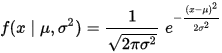


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· 实操Deepseek接入个人知识库
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· 【.NET】调用本地 Deepseek 模型
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库