归并排序
一、定义
基本思想
归并排序,其基本思想是合并2个已经排序的表,因为2个表已经排序,所以合并时,将数据放到第三个表中,则该算法可以通过对输入数据一样排序来完成。
- 基本的算法是取2个输入数组A和B,一个输出数组C。
- 3个计数器,Actr,Bctr,Cctr,他们初始置于对应数组的开始端。
- A[Actr]和B[Bctr]中较小者拷贝到C中的下一个位置,相关计数器向前推进一步。
- 当一个表有一个用完的时候,则将另一个表中剩余部分拷贝到C中。
图解
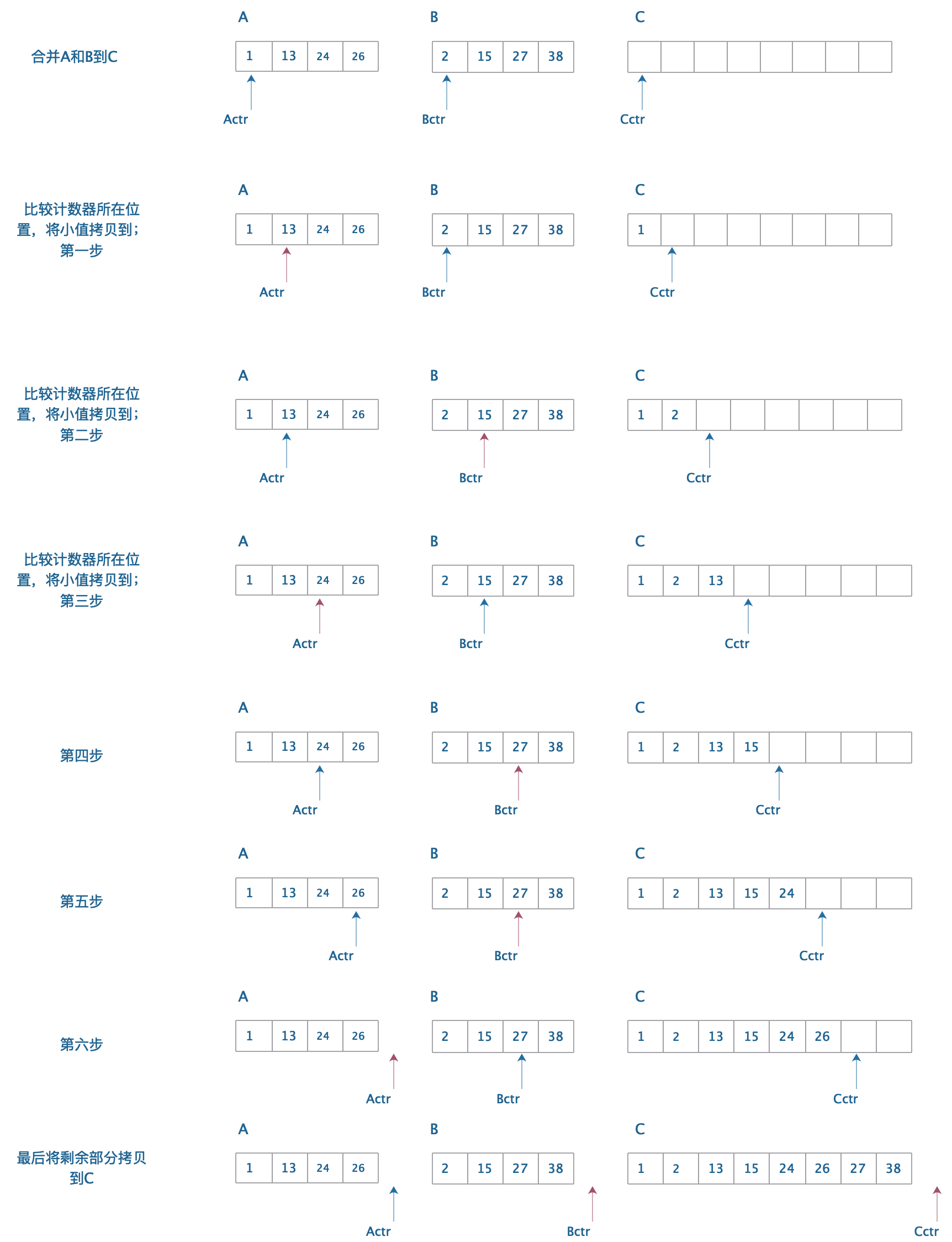
过程描述:
基本过程如图所示,将两个已经排序的数组进行合并。每次比较之后将小的元素拷贝到C,知道A指针到最后。B数组无从比较,因为A和B都已经排序,所以直接将B最后都数字拷贝到C。
编程描述
实际问题中,我们处理一个未排序的数组,怎么用它来实现排序呢,因为程序的目的是处理一个数组,而不是2个已排序的数组。例如,程序将数组a={24,13,26,1,2,27,38,15}排序,我们应当如何用程序描述这一过程。
这里采用一个实际经常使用的方法:分治策略
- 使用递归将前4个数字和后4个数字排序:1,13,24,26,2,15,27,38。
- 再合并这两部分。
二、算法分析
这里采用递归的程序实现,根据策略是分治的方法。而且是对半递归。我们可以很简单的分析其时间。
对上述公式的说明和求解:当N=1,即只有1个元素的时候,我们需要时间是1。当N个元素时,需要先处理前1/2和后面1/2。最后将所有的N拷贝一份。所以得到\(T(N)=2T(N/2)+N\)。
然后使用叠缩求和:将方程左边和右边相加,消去相等项,并且容易知道一共\(logN\)个方程。得到:
最后得到:\(T(N)=NlogN+N=O(NlogN)\)
结论
-
所以我们得到归并排序最后的时间为\(O(NlogN)\)。
-
但是它有一个明显的缺陷是:需要创建数组并拷贝。拷贝为常数时间,但是创建一个数组,额外增加了它的内存开销。
但是对数组的拷贝和内存的开辟,不同的语言是不一样的。例如:Java的引用对象排序时,拷贝数组,只是拷贝其对象的引用。只涉及到引用的赋值。所以归并排序作为Java范型排序的算法
而C++的范型排序则不同,如果拷贝的对象过于庞大,那会产生很大的时间和内存开销。是不能接受的。
三、代码地址
https://github.com/dhcao/dataStructuresAndAlgorithm/blob/master/src/chapterSeven/MergeSortEx.java


