优先队列(堆)·二项队列
一、 定义
我们知道，左式堆每次操作的时间界是\(O(logN)\)。二项队列支持合并、插入、删除最小值，每次插入的平均时间为常数时间，而最坏时间是\(O(logN)\)。
二项队列：
- 不是一棵堆序的树，而是堆序的树的集合，成为森林。
- 森林的每棵树都是二项树(binomial tree)。
- 每个高度上至多存在一棵二项树。
二、 结构
结构图解：
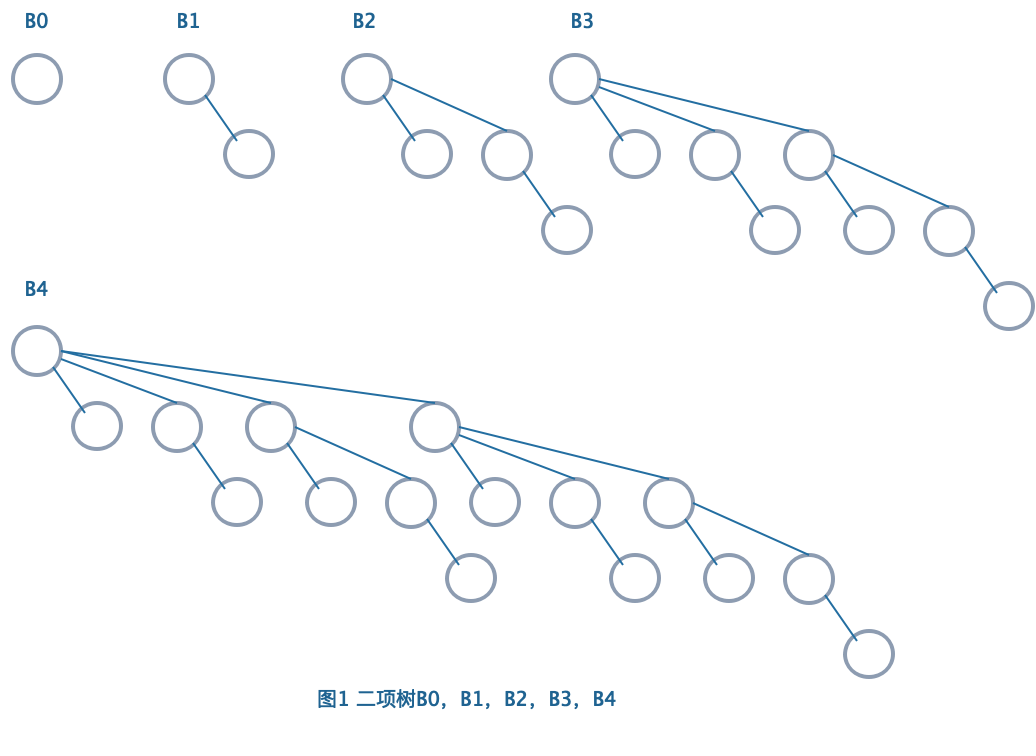
- 高度为0的二项树是一棵单节点树，例如B0。
- 高度为k的二项树\(B_k\)通过将一棵二项树\(B_{k-1}\)附接到另一棵二项树\(B_{k-1}\)的根上而构成。
结构描述：如上图
二项树\(B_{k}\)由一个带有儿子\(B_{0}\)，\(B_{1}\)，\(B_{2}\)，…，\(B_{k-1}\)的根组成！高度为k的二项树恰好有\(2^k\)个节点，而在深度\(d\)处的节点数是二项系数\(\binom{k}{n}\)。如果我们把堆序施加到二项树上并允许任意高度最多一棵二项树，那么就能够用二项树的集合表示任意大小的优先队列。例如大小为13的优先队列可以用森林\(B_3\)，\(B_2\)，\(B_0\)表示。可以记作1101，它不仅使用二进制表示了13的大小，而且也表达了这样的事实：在上述表示中，\(B_3\)，\(B_2\)，\(B_0\)出现，而\(B_1\)没有。
二项树组成的森林根二进制的关系：
数字13：森林表示为\(B_3\)，\(B_2\)，\(B_0\)；二进制记录为1101。
数字10：森林表示为\(B_3\)，\(B_1\)；二进制记录为1010。
三、 操作
二项队列中，最小元可以通过森林中所有的的树的根来找出。由于最多有\(logN\)棵不同的树，因此找到最小元的时间可以为\(O(logN)\)。如果我们记住最小元，并且在每次操作时更新它，那么可以直接操作最小元，时间为\(N\)。
3.1、 合并
合并两个二项队列在概念上是一个容易的操作。如下合并H1和H2。
合并图解：
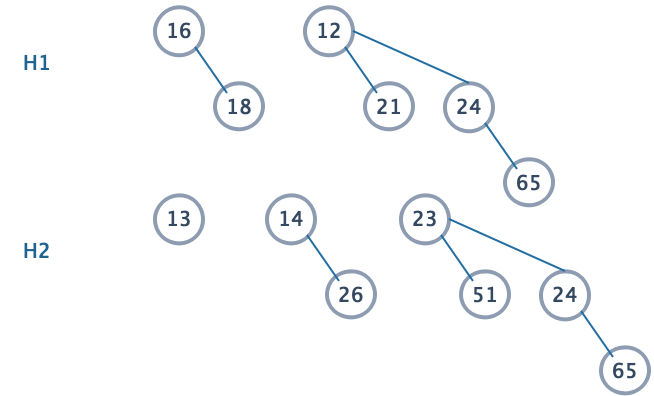
- 令\(H_3\)是新的二项队列，由于\(H_1\)没有高度为0的树而\(H_2\)有，我们让\(H_2\)中高度为0的树作为\(H_3\)的一部分。然后将两个高度为1的二项树相加。
- 将\(H_1\)和\(H_2\)的高度为1的二项树相加，让大的根成为小的根的子树，从而建立高度为2的二项树。
- 现在存在3棵高度为2的树，我们将合并其中2棵树，建立高度为3的二项树，这样，就只存在一棵高度为2，一棵高度为3，一棵高度为0的树组成的森林。
合并分析
几乎使用任意合理的实现方法合并2棵树均花费常数时间，而总共存在\(O(lonN)\)棵二项树，因此合并操作的最坏情形时间\(O(logN)\)。
关于时间界\(O(logN)\)
在N个节点组成的二项队列森林中，每个高度有且只有一棵树，很明显，高度\(h = logN\)，而合并操作本身花费常数时间，总个数\(O(logN)\)。很容得到以上时间界。
关于插入，插入其实就是合并一棵高度为0的二项树。关于插入的合并次数，如果元素将要插入的那个优先队列中不存在的最小二项树是\(B_i\)，那么运行时间与\((i+1)\)成正比。
关于插入的时间界：
为什么是\((i+1)\)的正比呢。假设：那么插入一个元素当作合并一个高度为0的二项树，记作\(C_0\)；
\(i = 1\)：森林中不存在\(B_1\)，那么最小树则是\(B_0\)，那么只需要合并\(B_0\)和\(C_0\)就能得到一棵高度为1的树，作为\(B_1\)。
\(i = 2\)：森林中不存在$B_2 \(，那么最小树则是\)B_1 \(，第一次发生在\)B_0\(和\)C_0\(，得到\)C_1\(。第二次合并发生在\)B_1\(和\)C_1\(，得到\)B_2$。
依次类推，我们可以知道\(i\)就是需要合并的次数。而1是插入时间。得到上述时间描述。
3.1、 删除最小值（deleteMin）
由于我们的二项队列中所有的二项树，均是堆序的。所以我们只需要比较所有树的根节点，就能找到最小值。关键在于，我们删除一棵高度为\(k\)的树的根节点，那么棵树会降级为多棵树，此时会打乱森林的顺序，我们需要重新整理森林里的树，重新得到二项队列。
删除图解：
- 删除二项队列H3中的最小值12，那么由H3解体得到\(H3-2\)，和原来的高度为0和1的树得到的\(H3-2\)。
- 得到2个二项队列：\(H3-1\)，\(H3-2\)。现在要做的就是将这个队列合并。
- 根据上文的合并法则，得到\(H4\)。
删除最小值本质上就是组建二项堆+合并二项堆。所以时间界依然是\(O(logN)\)。
关于这个时间界：
我们知道只要量级为改变，在大O模型中单纯的加减是不会影响我们对于时间算法的估计的。
四、 二项队列的实现
最重要的操作是deleteMin和merge。deleteMin需要快速找到最小值，因此需要一般树的标准表示方法。该操作还要求各个儿子按照他们的子树的大小排序。
合并树是我们需要将一棵树作为另一棵树的儿子被加到另一棵树上。由于这颗心树将是最大的子树，因此，以大小递减的方式保持这些子树是最好的。
实现方法：
-
二项树的每一个节点将包含数据、第一个儿子以及右兄弟
-
二项树中的各个儿子降秩次序排列。
如图：
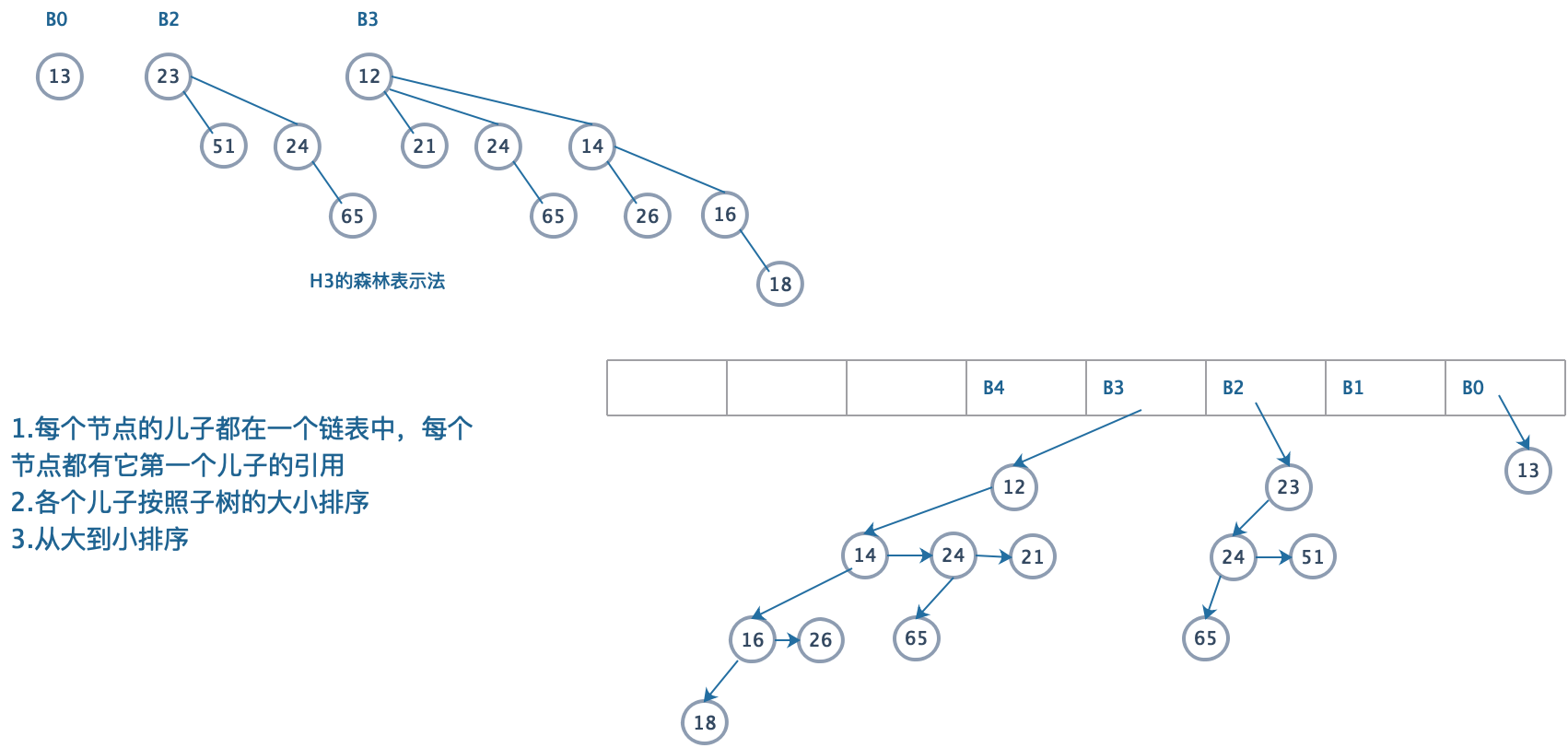
代码地址
....
