优先队列·二叉堆
一、定义
一般在优先队列里面说“堆”这个词，指的都是二叉堆这种数据结构实现。堆的最大结构特定是能很顺利的找到最小值！
堆是一棵完全二叉树，他总是满足，父节点的元素值小于其子节点的元素。并且每个子树都是堆！
-
堆是一棵完全二叉树
-
父节点元素小于(或等于)子节点元素
完全二叉树：https://baike.baidu.com/item/完全二叉树/7773232
除最底层外，其他层都是满二叉树结构。最底层节点顺序总是从左往右添加，一个父节点上添加节点时，优先添加左节点。
堆：https://www.cnblogs.com/dhcao/p/10574912.html
二、结构
2.1 结构图
已知堆是一棵完全二叉树，我们画一棵高度为3的堆。
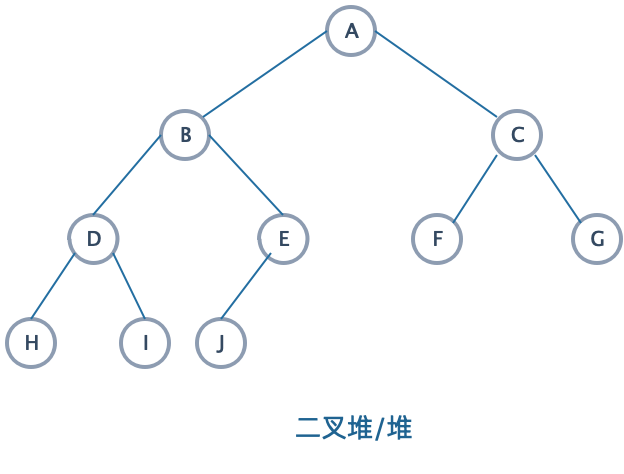
2.2 结构性质
容易证明，一棵高为\(h\)的完全二叉树有\(2^h\)到\(2^{h+1}\)-1个节点，这意味着完全二叉树的高是\(logN\)，显然他是\(O(logN)\)。
证明：
1.高度为\(h\)的满二叉树，有节点\(S_{max} = 2^{h+1}\)-1。
2.完全二叉树除最底层外，其他层是满二叉树。
3.不计算最底层，有节点有共\(S_{min} = 2^{h}\)-1。
4.由于高度是h，所以最底层最少有一个节点，所以范围为\([S_{min}+1,S_{max}]\)。
由于完全二叉树具有很明显的规律，所以我们可以用一个数组而不需要用链表来表示。我们设计一个数组来表示上图的“二叉堆/堆”。
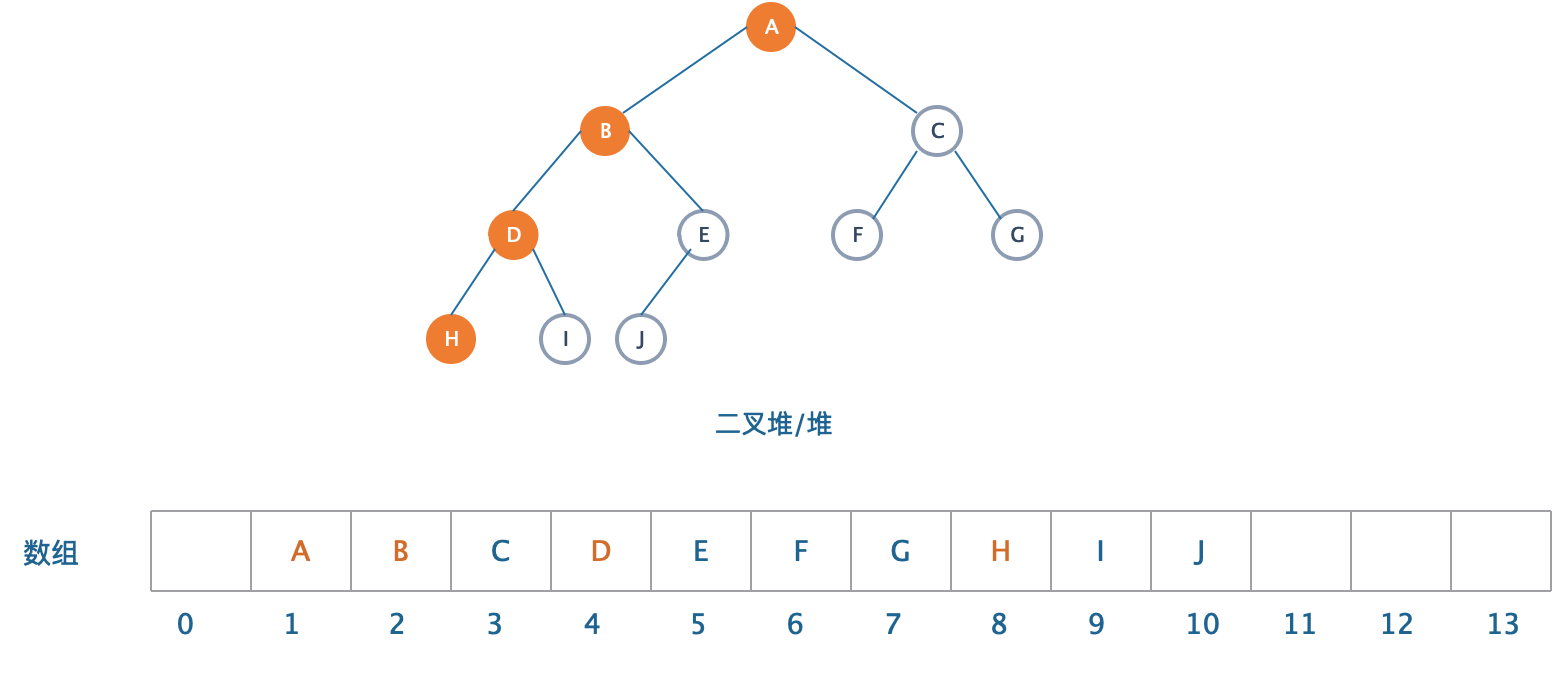
根据完全二叉树的性质，我们可以得到这样的数组来表示一个堆：
数组第0位放弃，从第一位开始放入二叉树的元素。我们看到，在堆中描述的父子结构（颜色标记），在数组中依然得以保留，不过保留的方式变成了：第\(i\)个位置上的元素，他的左儿子总是在第\(2i\)位置上，右儿子在\(2i+1\)的位置上！。
2.3 结构说明：
因此，一个堆结构将由一个数组和一个代表当前堆大小的整数构成。
三、堆序性质
3.1 堆序性质
堆序性质是让堆操作快速执行。我们设计堆的初衷是为了快速找出最小元素。所以堆序性质应该也能满足这个目的，我们设定堆的最小元素在根节点，如果把任意子树都当作堆结构，那么可以得到：堆父节点的值总是小于(或等于)子节点。
3.2 简单图解
不满足二叉堆堆序性质，完全二叉树就不是堆！
四、堆操作
4.1 插入 （insert）
根据堆的特性，我们每次插入都需要保证满足堆的堆序特性。所以很多时候我们在插入之后，不得不调整整个堆的顺序来维持堆的数据结构。
4.1.1 上滤：
为将一个元素X插入到堆中，我们在下一个可用位置创建一个空穴，否则该堆将不再是完整树，如果X可以放在该空穴中而不破坏堆的序，那么可以插入完成。否则，我们把空穴的父节点 上的元素移入该空穴中，这样，空穴就朝着根的方向冒一步，继续该过程直到X能被放入空穴为止。
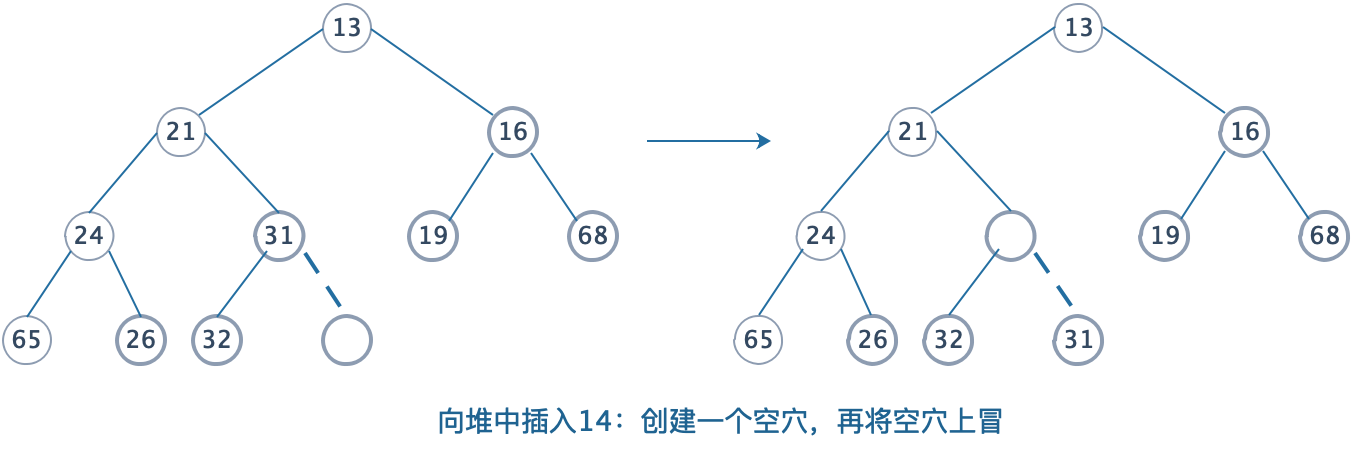
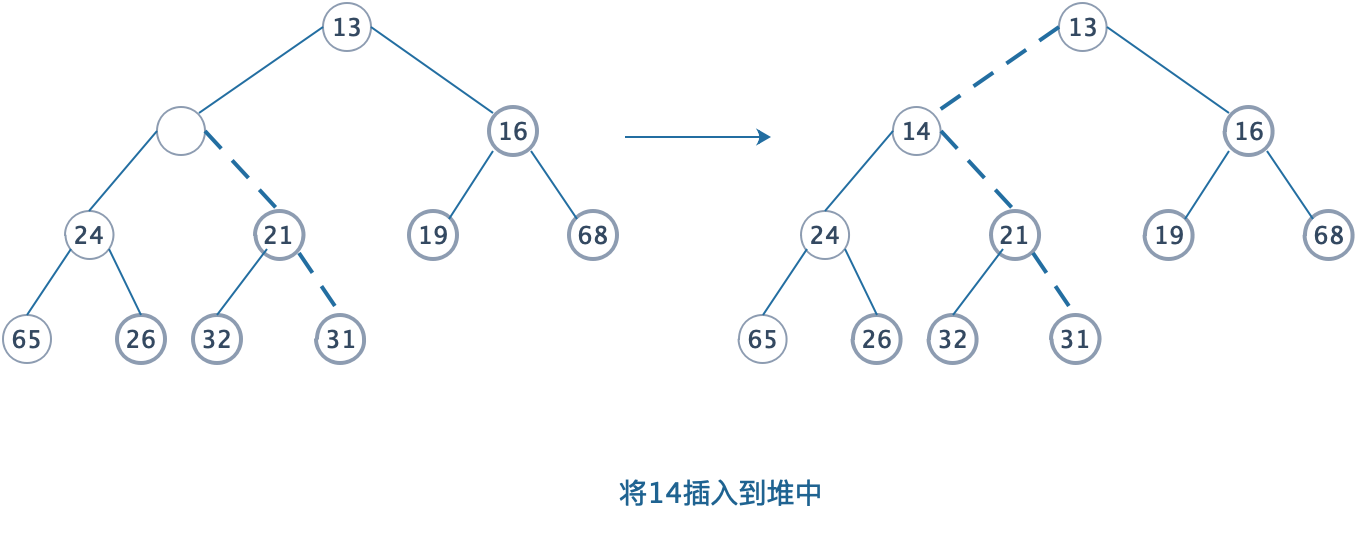
4.1.2 操作说明
我们可以反复的交换操作，直到建立正确的堆序来实现上滤插入。这个操作我们可以通过递归来实现。如果我们要插入的新的值是最小元素，我们需要一只上滤到根节点。那么这种插入到时间是\(O(N)\)。不过在实际中早已经证明，执行一次插入平均需要2.607次比较，因此平均上移元素1.607层。
插入一次需要上移动N层，加上一次插入时间。所以插入总时间是上移时间+插入程序执行时间。
4.2 删除最小元素（deleteMin）
根据堆堆特性，找到最先元素很简单，就是树的根节点，但是删除它却不容易，删除根节点，必然会破坏树的结构。
4.2.1 下滤
删除一个元素，我们可以很快找到，根节点元素就是最小的元素。我们删除根节点后，根据完全二叉树的性质，我们必然要移动最后一个节点。最后一个节点成为X，如果X能被放到空穴中(此时空穴在根节点)，那么deleteMin完成，不过这一般不太可能，因为我们将空穴的儿子中较小者放到空穴中，这样把空穴向下推了一层，重复该动作直到X可以被放大空穴中。
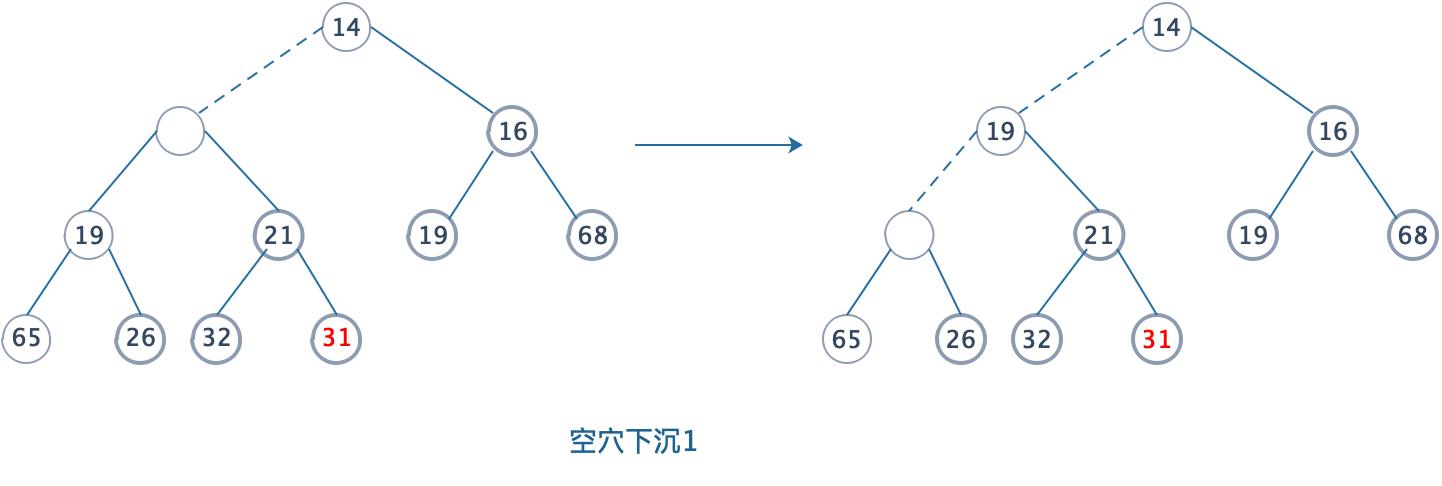
4.2.2 操作说明
其实我们可以当作将最后一个节点放到根节点，然后从根节点开始下滤，进行位置调整。我们通过反复的交换空穴位置，直到将最后一个值能够插入到空穴，递归可以帮我们做到这点。同上滤一样，最坏情况依然是\(O(N)\)。平均时间是\(O(logN)\)。
这里有个小说明，我们将最后一个节点放到根节点时，并不是做交换，因为根节点被舍弃，我们直接赋值就可以。会减少操作时间。
4.3 构建堆
构建N个元素的二叉堆，我们直接执行N次insert方法即可， 因为在设计insert方法时，就已将考虑到将插入到值放到堆的合适位置。输入N项，即可自动生成N大小的堆。
一般的算法时将N项以任意顺序放入树中，保持结构特性，然后按顺序对所有节点进行下滤。
稍微解释下我们在代码中的下滤做法。
// 代码在文章最后
/**
* 构建
*/
private void buildHeap() {
for (int i = currentSize / 2; i > 0; i--) {
percolateDown(i);
}
}
我们选取 \(i = currentSize/2\)，之所以是这个值，是因为\(array[currentSize]\)为最后一个节点， \(i = currentSize/2\) 得到的是倒数第二层最后一个节点的父节点，正如上图中的节点 21，我们从倒数第二层开始下滤，而不需要从最后一层进行，因为我们只在乎父子节点的大小关系。
代码位置
https://github.com/dhcao/dataStructuresAndAlgorithm/blob/master/src/chapterSix/BinaryHeap.java
