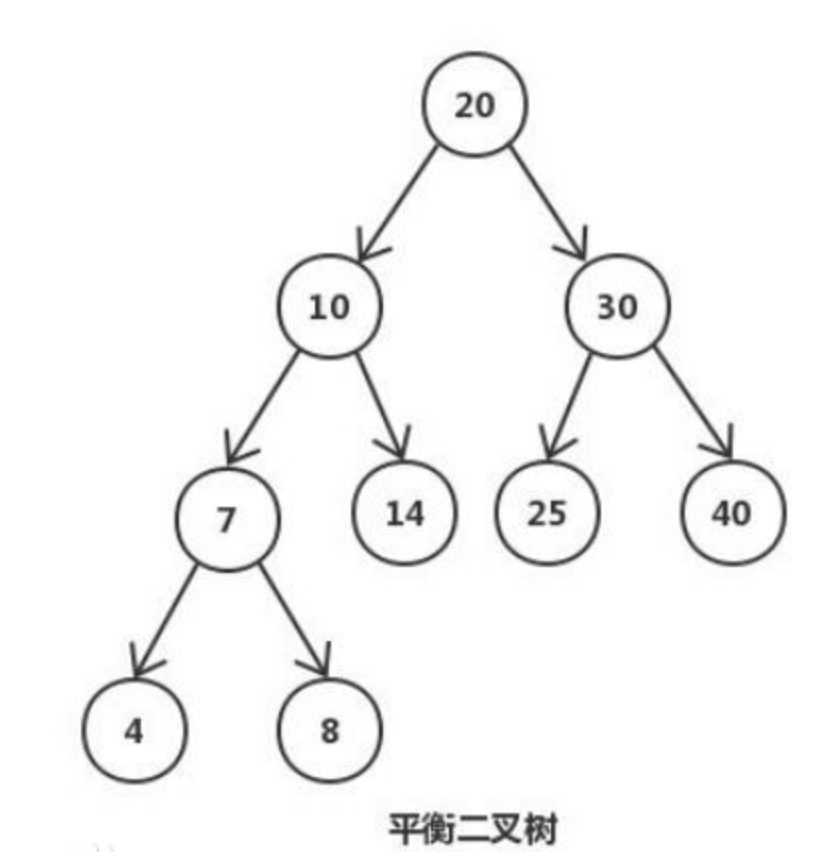
树·AVL树/平衡二叉树

1、AVL树

　　带有平衡条件的二叉查找树，所以它必须满足条件：

　　1 是一棵二叉查找树

　　2 满足平衡条件

　1.1 平衡条件：

　　1）严格的平衡条件：每个节点都必须有相同高度的左子树和右子树（过于严格而不被使用）。

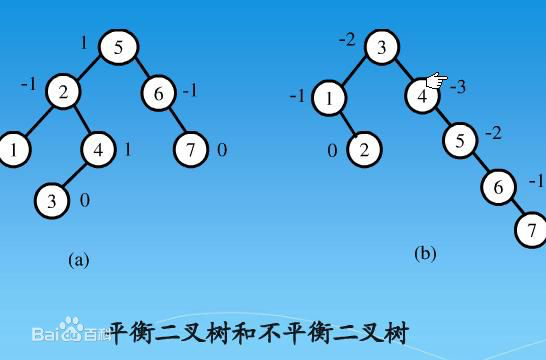
　　2）AVL树的平衡条件：每个节点的左子树和右子树的高度最多差1的二叉查找树（空树的高度定义为-1）

　1.2 特点：

　　严格的高度平衡，使得AVL树在查找时耗费时间更少。它理论上的时间复杂度为O(logN)。

　　虽然二叉查找树的平均时间也为O(logN)，但是二叉查找树并不平衡，它的最坏情况是所有的子节点都只含有左子树，或者都只含有右子树，这种情况下，它的查找耗费的时间为O(N)。而平衡的AVL树可以避免这种极端情况。

                                                                 

 

2、AVL树的高度和最少节点个数S(h)的函数

 　　2.1）假设一棵AVL树的最少节点数为S(h)，h为树的高度。

　　 2.2) 根据平衡条件，左右子树的高度最多差1，假设左子树的高度为h-1，右子树的高度为h-2。

　　 2.3）根据2.2假设，节点总数=左子树节点数+右子树节点数+1。  ==》  S(h) = S(h-1) + S(h-2) +1

　　根据斐波拉契数可知，AVL树的节点个数与该数列密切相关。

　　　　　　高度为h的AVL树的最少节点总数：S(h) = S(h-1) + S(h-2) +1

 

3、维持AVL的平衡条件：旋转

　　根据AVL树的定义，它是带有平衡条件的查找树。平衡条件限制了它的每个节点的左右子树的高度差不能大于1，那么对于二叉树来说，插入操作是经常会出现的。当向一棵树插入一个节点时，难免会破坏AVL树的平衡条件，

　　比如：

　　　　　　　　　　　　　　　　　　　　

 

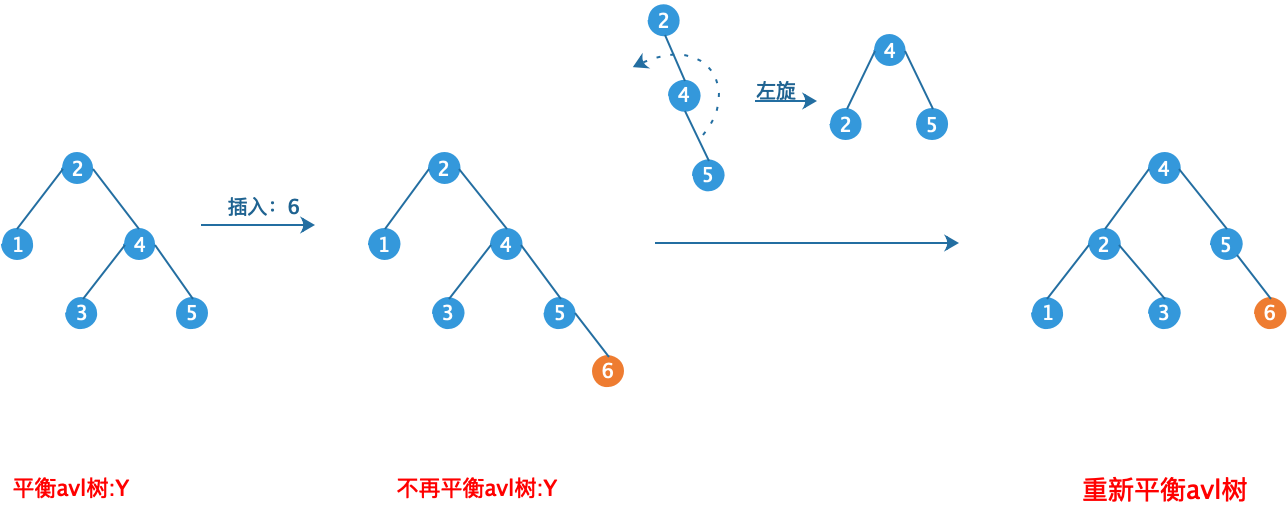
　　在左图的AVL树中插入节点6，根据查找树的插入条件，节点6只能作为节点7度左子树。那么对于以8为父节点的子树来说，8的左子树的高度为2，右子树的高度为0，相差大于1。所以右图不再是AVL树。即失去了其存在的优势，不平衡的二叉查找树，时间复杂度增加。

　　所以我们需要在插入节点时，重新校验树的平衡条件，在必要时调整树的结构，使其保持为AVL树。这个简单的调整，我们称之为旋转！

　　我们把需要重新平衡的节点称为α（如上图的节点8），二叉树最多只有2个节点，而且不满足平衡条件，则α节点的左右子树高度差为2。容易看出，这种不平衡可能出现在下面4种情况。

　　1.对α的左儿子的左子树进行一次插入。（如上图，对节点8的左儿子7的左子树6进行一次插入）

　　2.对α的左儿子的右子树进行一次插入。

　　3.对α的右儿子的左子树进行一次插入。

　　4.对α的右儿子的右子树进行一次插入。 

对于第1，4种情况，我们可以用单旋转进行平衡，对于2，3种情况，我们用双旋转进行平衡。

 

4、单旋转 

　　很多时候，对于旋转还有另一种说法，左旋和右旋。顺便解释一下单旋转，双旋转，左旋，右旋的联系和区别。

　　1、第一种情况：对α的左儿子的左子树进行一次插入。

　　　                                                  　

　　　　在原来的平衡AVL树上增加节点f，如上图！可见在增加了节点f之后，对应情况，对a节点的左儿子b的左子树c进行插入f。让a节点变得不再是平衡AVL树，这时候，我们对a树进行操作，使得它重新平衡。

　　操作的原理：我们把过深的树上移一层，把高层往下移一层。使之重新平衡。

　　　　如图：

　　　　　　

 

                               

 

　　讲解：在x树中，开始是平衡的，在左子树进行插入之后不再，x树不再平衡。为了使得x树平衡，我们采用的是右旋方法，旋转不平衡的子树，使得重新平衡。此处采用右旋一次，叫做单旋转。

　　2、第二种情况：对α的右儿子的右子树进行一次插入。

　　这种情况跟第一种一个样子。如图：对一棵平衡二叉树插入5，6两个节点。

　　　　　　　　 

                             

 

　　

 

 

                         

 

 

5、双旋转

　　顾名思义：双旋转要用到左旋和右旋的组合，或者单方向2次旋转。

　　3、第三种情况：对α的右儿子的左子树进行一次插入。

　　　如图：简单双旋转　　

      

　　讲解：在插入节点15之后，Z树变得不再平衡，这时，我们采用左旋或者右旋都明显的不能让树重新平衡，所以结合起来使用。我们的目的，是使得右子树降低一层高度。如果我们能使用左旋或者右旋即可达到目的，但是现在的样子明显不行，所以第一次旋转的目标：使得树可以使用一次旋转而重新平衡。为了让节点7，15，16重新排列，我们假设存在虚拟节点C，帮助我们理解第一次右旋。而后再进行左旋。所以这是一次“右-左双旋转”！　

　　4、第四种情况：对α的左儿子的右子树进行一次插入。　

　　如图，在上述平衡树上插入节点：14； 

　　　　 

     

6、Java描述单旋转和双旋转：

　　代码地址：

https://github.com/dhcao/dataStructuresAndAlgorithm/tree/master/src/chapterFour

　　单旋转：右旋

/**
 * desc:看懂上面的图，再看代码：参看第一种。
 * 假设：k2树不再平衡，在k2的左儿子k1的左子树进行插入，导致k2子树不再平衡。采用右旋转
 * 右旋转：
 * 1.用k2的左子树k1来代替k2的位置。（k2丢失左子树）
 * 2.让k2成为k1的右子树。
 * 3.k1的右子树，重新成为k2的左子树。
 *
 * @auther:  dhcao
 */
private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2) {

   AvlNode<T> k1 = k2.left;

   k2.left = k1.right;
   k1.right = k2;
   // height方法返回该子树的 高
   k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
   k1.height = Math.max(height(k1.left), k2.height) + 1;
   return k1;
}

 

 　　双旋转：右-左双旋

private AvlNode<T> doubleWithLeftChild(AvlNode<T> k3) {
		k3.left = rotateWithLeftChild(k3.left);
		return rotateWithLeftChild(k3);
	}