信息安全与数学基础-笔记-③一次同余方程

知识目录

• 一次同余方程的解
• 中国剩余定理
• 中国剩余定理的应用

一次同余方程的解

---

本文只研究一次同余方程的解。

---

f(x) 三 0 (mod m)，
若有一个s能够满足该式子，那么该数字就是该式子的解，
在同余方程式中的解一般写成：x三s (mod m)

• 同余方程式中的解释剩余类，不同解即不同剩余类，一个解代表一个剩余类
• 设：f(x) = ax, ax 三 1 (mod m) ,若(a,m) 三 1, 则 ax 三 1 (mod m)一定有唯一一个解。
  解释：因为am互素，所以ax 三 1 该公式就是一个求逆的公式，使用欧几里德算法后再裴蜀等式求逆即可求出 sa + tm = 1 ，所以s就是x的唯一解。
• 同上一条差不多，若 ax 三 b (mod m) ,若(a,m) 三 1，则则 ax 三 1 (mod m)一定有唯一一个解。
  解释：上面两条为啥有唯一一个解？因为解是剩余类，所以我们在完全剩余系中找解是必然的，所以解必然是（0，1，2，3…m-1）又因为我们式子中乘了a，所以完全剩余系中全部乘a也无伤大雅，仍旧是完全剩余系，（a0，a1，a2，a3…a(m-1)），然后观察该变化后的剩余系，我们要找出ax=1的解，必然在该剩余系中，而且只有一个，因为完全剩余系中都是互素的，因此只有唯一一个解。

---

ax 三 b (mod m)如何求解？
下面两种都必须判断a和m除去最大公因数后是否互素

• 一：求有多少个解
  （a,m）= d ，d即为解数
• 二：化简方程式
  a/d * x 三 b / d (mod m/d),同时除以最大公因数
• 三：按照最简单的方法求解
  先求出a/d * x 三 1 (mod m/d)的唯一一个解，假设为：$x_0$
  然后特解就是：$x_0$ * b / d
• 四：我们知道了一个，需要求出其他解
  那么通解就是可以表示所有解，通解即：
  $x_0$* b / d + m/d * t （ t = 0,1…(m-1) ），很明显当t = 0的时候就是特解。
• 总结
  

中国剩余定理

方程式形如↓：

• 方程式条件：
  1：$m_i$之间必须是两两互素
  2：x的系数必须是1
  
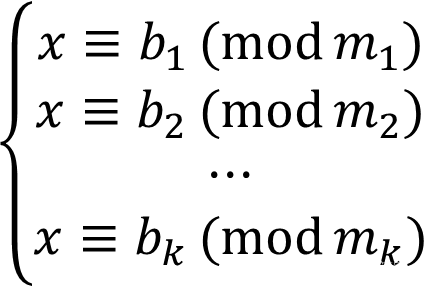
  因为x的系数都必须为1，这种方程式解只有一个
• 如何求解？
  第一步，先令：
  

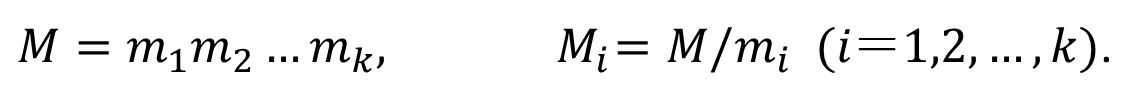
第二步：（把数带进去求解一次同方程式即可）

说明：我们的M${}_i$${}^{-}$${}^1$是M${}_i$模m${}_i$下求出来的逆也就是说：
M${}_i$${}^{-}$${}^1$ × M${}_i$ 三 1 （mod m${}_i$）

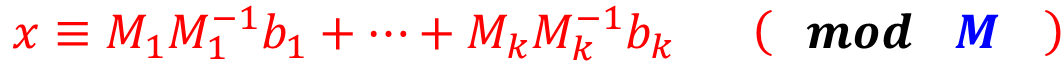
• 假设$m_i$之间不是两两互素的如何求解
  比如：
  
  这时候我们可以选择将模数拆开分解
  
  将上面的式子化简得：
  
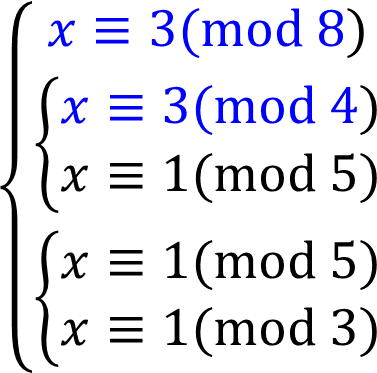
  观察到：x三1有两个，因为模数不一样，最后却选择了mod 8
  解释：因为mod 8的解和mod 4的解有重合的地方，但因为mod 4 的解是比mod 8的解的个数多，并且有的不符合mod 8的解，所以我们选择mod 8的，因为这样mod 8的解也能用于mod 4的解，两者通用。
  因此最后拆解的结果为：
  

• 假设x的系数不是全都为1
  

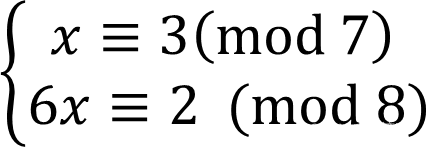
我们先将系数不是为1的式子先单独求出他的解，很明显就是：

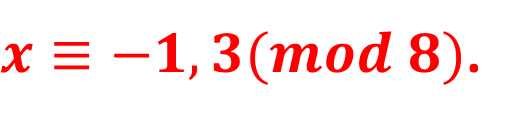
然后再拆成两个方程式分别求解：

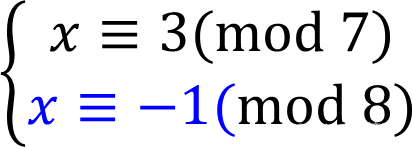
第一个方程式解为：

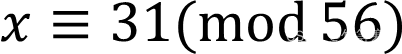
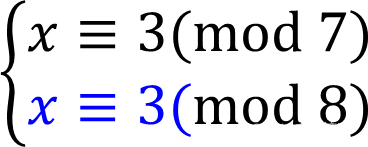
第二个方程式解为：

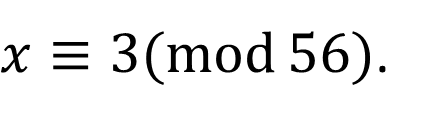
中国剩余定理的应用

当我们计算$5^1$${}^0$${}^0$${}^0$${}^0$(mod 391) 的时候计算量很大
这时候发现391=17×23
利用这个分解因子

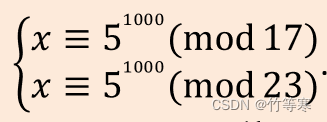
因为5和另外两个模数都是互素，并且两个模数也是素数，所以直接使用欧拉定理将次幂减少

最后解同余方程组即可，使用中国剩余定理：

---

over.

---