leetcode刷题总结901-950

901. 股票价格跨度　　

　　描述：
　　　　

 

 

 　　思路：单调栈。

　　　　

class StockSpanner {
    Stack<Integer> prices, weights;

    public StockSpanner() {
        prices = new Stack();
        weights = new Stack();
    }

    public int next(int price) {
        int w = 1;
        while (!prices.isEmpty() && prices.peek() <= price) {
            prices.pop();
            w += weights.pop();
        }

        prices.push(price);
        weights.push(w);
        return w;
    }
}

904. 水果成篮

　　描述：

　　　　

 

 

 　　思路：问题可以看成  最长连续子序列。序列中最多包含两种元素。

907. 子数组的最小值之和

　　描述：

　　　　

 

 

 　　思路：

　　　　

class Solution {
    public int sumSubarrayMins(int[] A) {
        int MOD = 1_000_000_007;

        Stack<RepInteger> stack = new Stack();
        int ans = 0, dot = 0;
        for (int j = 0; j < A.length; ++j) {
            // Add all answers for subarrays [i, j], i <= j
            int count = 1;
            while (!stack.isEmpty() && stack.peek().val >= A[j]) {
                RepInteger node = stack.pop();
                count += node.count;
                dot -= node.val * node.count;
            }
            stack.push(new RepInteger(A[j], count));
            dot += A[j] * count;
            ans += dot;
            ans %= MOD;
        }

        return ans;
    }
}

class RepInteger {
    int val, count;
    RepInteger(int v, int c) {
        val = v;
        count = c;
    }
}

 

910. 最小差值 II

　　描述：
　　　　

 

 

 　　思路：关键一点就是，在某一个节点，之前的数全部加K，之后的数全部减K

　　　　

 

 

 915. 分割数组

　　描述：

　　　　

 

 

 　　思路：辅助数组存储左边最大的元素。

918. 环形子数组的最大和

　　描述：

　　　　

　　思路：　　　

import java.util.Arrays;

public class Solution {

    public int maxSubarraySumCircular(int[] A) {
        int len = A.length;
        // 特例判断
        if (len == 0) {
            return 0;
        }
        if (len == 1) {
            return A[0];
        }

        int maxSubArray = maxSubArray(A);
        int minSubArrayExcludeHeadAndTail = minSubArray(A);

        int sum = 0;
        for (int value : A) {
            sum += value;
        }
        return Math.max(maxSubArray, sum - minSubArrayExcludeHeadAndTail);
    }

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        // dp[i]：以 nums[i] 结尾的「连续」子区间的最大和
        int[] dp = new int[len];
        dp[0] = nums[0];

        for (int i = 1; i < len; i++) {
            if (dp[i - 1] >= 0) {
                dp[i] = dp[i - 1] + nums[i];
            } else {
                // dp[i - 1] < 0 的时候，前面的部分丢弃
                dp[i] = nums[i];
            }
        }

        // 全局扫一遍，找到最大值
        int res = dp[0];
        for (int i = 1; i < len; i++) {
            res = Math.max(res, dp[i]);
        }
        return res;
    }

    public int minSubArray(int[] nums) {
        // 思路和 maxSubArray 完全一致，求最大的地方改成最小
        // 但这里求的区间和不包括头和尾
        int len = nums.length;

        // dp[i]：以 nums[i] 结尾的「连续」子区间的最小和
        int[] dp = new int[len];
        dp[0] = nums[0];

        // 注意 i 的下标
        for (int i = 1; i < len - 1; i++) {
            if (dp[i - 1] >= 0) {
                // 加上前面的数，会使得结果更大，因此前面的部分丢弃
                dp[i] = nums[i];
            } else {
                dp[i] = dp[i - 1] + nums[i];
            }
        }

        // 全局扫一遍，找到最小值
        int res = dp[0];
        for (int i = 1; i < len; i++) {
            res = Math.min(res, dp[i]);
        }
        return res;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        // int[] A = {1, -2, 3, -2};
        // int[] A = {5, -3, 5};
        int[] A = {3, -1, 2, -1};
        int res = solution.maxSubarraySumCircular(A);
        System.out.println(res);
    }
}

　　　　分两种情况，一种为没有跨越边界的情况，一种为跨越边界的情况

　　　　没有跨越边界的情况直接求子数组的最大和即可；
　　　　跨越边界的情况可以对数组求和再减去无环的子数组的最小和，即可得到跨越边界情况下的子数组最大和；

　　　　

921. 使括号有效的最少添加

　　描述：

　　　　

 

 

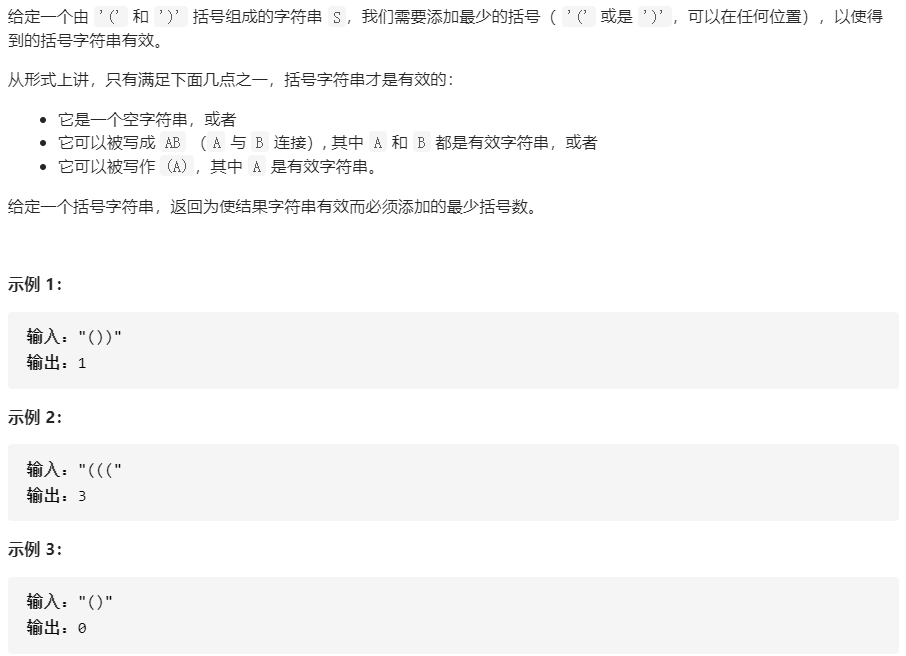
 　　思路：栈

class Solution {
public:
    int minAddToMakeValid(string S) {
        stack<char> temp;
        for(int i=0;i<S.size();i++)
        {
            if(temp.empty())
            {
                temp.push(S[i]);
            }
            else{
                if(S[i]==')'&&temp.top()=='(')
                {
                    temp.pop();
                }
                else{
                    temp.push(S[i]);
                }
            }
        }
        return temp.size();
    }
};

923. 三数之和的多种可能

　　描述：

　　　　

 

 

 　　思路：可以通过hashmap  <num,count>完成。

　　　　也可以通过动态规划。 dp[n][j][k]表示前n个数中某j个数的和为k的个数。

　　　　首先，dp[i][j][k]表示考虑前i个数时，从中选出j个数，组成k大小的方案数。这里的定义是从01背包的定义拓展而来的，这里加入了一个约束限制，就是要从前i个数中选出j个数组成k大小。这样的好处是，如果选择最后一个数，则根据定义的最优子结构性质，可以很简单的使用dp[i - 1][j - 1][k - A[i]]来计算当前除去最后一个数的总共选法数；如果不选择最后一个数，则直接加上不选择的数量个数，即dp[i - 1][j][k]。

926. 将字符串翻转到单调递增

　　描述：

　　　　

 

 

 　　思路：

　　　　dp[i][0]，dp[i][1] 分别代表字符 S[i] 最终选择 0 和 1 的最少翻转次数，
　　　　考虑到递增，那么 dp[i][0] 只能由 dp[i-1][0] 转化而来，所以，状态转移方程如下：

　　　　如果 S[i] 是 '1':
　　　　dp[i][0] = dp[i-1][0] + 1 # 只能从 0 转化来，翻转 '1' 为 '0'，翻转次数加 1
　　　　dp[i][1] = min(dp[i-1][0], dp[i-1][1]) # 已经为 '1'，无需翻转

　　　　如果 S[i] 是 '0':
　　　　dp[i][0] = dp[i-1][0] # 只能从 0 转化来，无需翻转
　　　　dp[i][1] = min(dp[i-1][0] + 1, dp[i-1][1] + 1) # 翻转 '0' 为 '1'，翻转次数加 1

class Solution:
    def minFlipsMonoIncr(self, S: str) -> int:
        zero, one = 0, 0
        for c in S:
            if c == '1':
                one, zero = min(zero, one), zero + 1
            else:
                one = min(zero + 1, one + 1)
        return min(zero, one)

930. 和相同的二元子数组

　　描述：

　　　　

　　思路：前缀和+hash.

931. 下降路径最小和

　　描述；
　　　　

 

 　　思路：动态规划，从底向上。

939. 最小面积矩形

　　描述：

　　　　

 

 　　思路：将所有点放入集合中，并枚举矩形对角线上的两个点，并判断另外两个点是否出现在集合中。例如我们在枚举到 (1, 1) 和 (5, 5) 时，我们需要判断 (1, 5) 和 (5, 1) 是否也出现在集合中。

945. 使数组唯一的最小增量

　　描述：

　　　　

 

 　　思路：

class Solution {
    public int minIncrementForUnique(int[] A) {
        // 先排序
        Arrays.sort(A);
        int move = 0;
        // 遍历数组，若当前元素小于等于它的前一个元素，则将其变为前一个数+1
        for (int i = 1; i < A.length; i++) {
            if (A[i] <= A[i - 1]) {
                int pre = A[i];
                A[i] = A[i - 1] + 1;
                move += A[i] - pre;
            }
        }
        return move;
    }
}

946. 验证栈序列

　　描述；
　　　　

 

 　　思路：

class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        int N = pushed.length;
        Stack<Integer> stack = new Stack();

        int j = 0;
        for (int x: pushed) {
            stack.push(x);
            while (!stack.isEmpty() && j < N && stack.peek() == popped[j]) {
                stack.pop();
                j++;
            }
        }

        return j == N;
    }
}

948. 令牌放置

　　描述：L　　　　

　　　　

 

 　　思路：如果让我们来玩令牌放置这个游戏，在让令牌正面朝上的时候，肯定要去找能量最小的令牌。同样的，在让令牌反面朝上的时候，肯定要去找能量最大的令牌。

class Solution {
    public int bagOfTokensScore(int[] tokens, int P) {
        Arrays.sort(tokens);
        int lo = 0, hi = tokens.length - 1;
        int points = 0, ans = 0;
        while (lo <= hi && (P >= tokens[lo] || points > 0)) {
            while (lo <= hi && P >= tokens[lo]) {
                P -= tokens[lo++];
                points++;
            }

            ans = Math.max(ans, points);
            if (lo <= hi && points > 0) {
                P += tokens[hi--];
                points--;
            }
        }

        return ans;
    }
}