leetcode刷题总结851-900

851. 喧闹和富有

　　描述：
　　　　

 

 

 　　思路：深度优先（带记忆）。  这个题有点秒。。

853. 车队

　　描述：

　　　　

 

 

 　　思路：

　　　　我们首先对这些车辆按照它们的起始位置降序排序，并且用 (target - position) / speed 计算出每辆车在不受其余车的影响时，行驶到终点需要的时间。对于相邻的两辆车 S 和 F，F 的起始位置大于 S，如果 S 行驶到终点需要的时间小于等于 F，那么 S 一定会在终点前追上 F 并形成车队。这是因为在追上 F 之前，S 的行驶速度并不会减小，而 F 却有可能因为追上前面的车辆而速度减小，因此 S 总能在终点前追上 F。

854. 相似度为 K 的字符串

　　描述：

　　　　

 

 

 　　思路：

class Solution {
public:

    int res , n ;

    void dfs(int pos , int step , string& A , string &B) {
        if (step >= res)
            return ;
        if (pos == n) {
            res = min(res , step) ;
            return ;
        }
        if (A[pos] == B[pos]) {
            dfs(pos + 1 , step , A , B) ;
        } else {
            for (int i = pos + 1 ; i < n ; ++i) {
                if (A[i] == B[pos] && A[i] != B[i]) {
                    swap(A[i] , A[pos]) ;
                    dfs(pos + 1 , step + 1 , A , B) ;
                    swap(A[i] , A[pos]) ;
                }
            }
        }
    }

    int kSimilarity(string A, string B) {
        n = A.length() ;
        res = n + 1 ;
        dfs(0 , 0 , A , B) ;
        return res ;
    }
};

856. 括号的分数

　　描述：

　　　　

 

 

 　　思路：栈

861. 翻转矩阵后的得分

　　描述：

　　　　

 

 

 　　思路：

　　　　先横竖变换保证第一列全部是1
　　　　竖变换保证其他列1比0多

 

 

862. 和至少为 K 的最短子数组　　

　　描述：

　　　　

 

 

 　　思路：前缀和。然后进行双指针判断。

863. 二叉树中所有距离为 K 的结点

　　描述：

　　　　

 

 

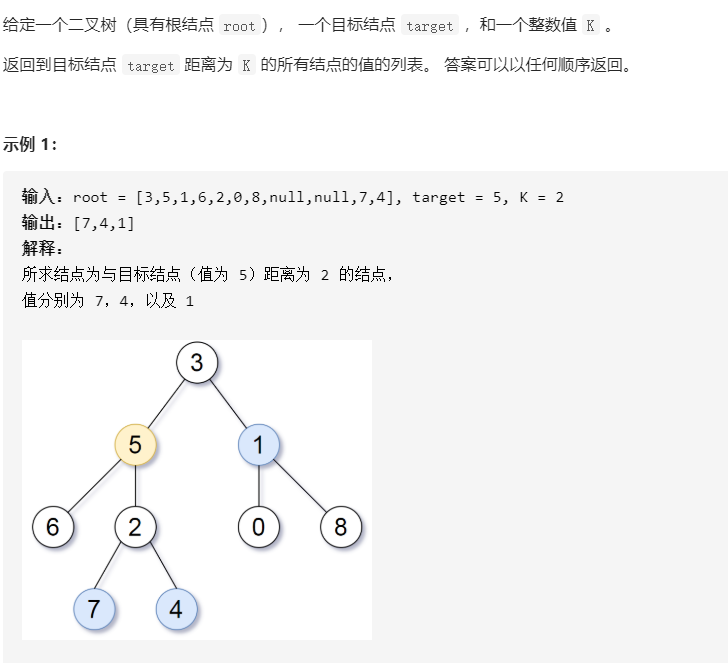
 　　思路：对于tartget进行深度优先，。

866. 回文素数

　　描述：

　　　　

 

 

 　　思路：

　　　　　　

class Solution {
    public int primePalindrome(int N) {
        while (true) {
            if (N == reverse(N) && isPrime(N))
                return N;
            N++;
            if (10_000_000 < N && N < 100_000_000)
                N = 100_000_000;
        }
    }

    public boolean isPrime(int N) {
        if (N < 2) return false;
        int R = (int) Math.sqrt(N);
        for (int d = 2; d <= R; ++d)
            if (N % d == 0) return false;
        return true;
    }

    public int reverse(int N) {
        int ans = 0;
        while (N > 0) {
            ans = 10 * ans + (N % 10);
            N /= 10;
        }
        return ans;
    }
}

 

869. 重新排序得到 2 的幂

　　描述：

　　　　

 

 

 　　思路：排列组合问题。 。。。回溯算法。

　　　　

class Solution {
    public boolean reorderedPowerOf2(int N) {
        // Build eg. N = 128 -> A = [1, 2, 8]
        String S = Integer.toString(N);
        int[] A = new int[S.length()];
        for (int i = 0; i < S.length(); ++i)
            A[i] = S.charAt(i) - '0';
        return permutations(A, 0);
    }

    // Return true if A represents a valid power of 2
    public boolean isPowerOfTwo(int[] A) {
        if (A[0] == 0) return false;  // no leading zero

        // Build eg. A = [1, 2, 8] -> N = 128
        int N = 0;
        for (int x: A)
            N = 10 * N + x;

        // Remove the largest power of 2
        while (N > 0 && ((N & 1) == 0))
            N >>= 1;

        // Check that there are no other factors besides 2
        return N == 1;
    }

    /**
     * Returns true if some permutation of (A[start], A[start+1], ...)
     * can result in A representing a power of 2.
     */
    public boolean permutations(int[] A, int start) {
        if (start == A.length)
            return isPowerOfTwo(A);

        // Choose some index i from [start, A.length - 1]
        // to be placed into position A[start].
        for (int i = start; i < A.length; ++i) {
            // Place A[start] with value A[i].
            swap(A, start, i);

            // For each such placement of A[start], if a permutation
            // of (A[start+1], A[start+2], ...) can result in A
            // representing a power of 2, return true.
            if (permutations(A, start + 1))
                return true;

            // Restore the array to the state it was in before
            // A[start] was placed with value A[i].
            swap(A, start, i);
        }

        return false;
    }

    public void swap(int[] A, int i, int j) {
        int t = A[i];
        A[i] = A[j];
        A[j] = t;
    }
}

 

 

870. 优势洗牌

　　描述：

　　　　

 

 

 　　思路：贪心。田忌赛马

　　　　

class Solution {
    public int[] advantageCount(int[] a, int[] b) {
        int n = b.length;
        Arrays.sort(a);
        int[][] pair = new int[n][2];
        for (int i = 0; i < n; i ++)
            pair[i] = new int[]{b[i], i};//把下标保存下来
        Arrays.sort(pair, (x, y)->x[0] - y[0]);

        int[] res = new int[n];
        for (int i = 0, r = n - 1, l = 0; i < n; i ++)//r最大值，l标明最小值；
        {
            if (a[i] <= pair[l][0]) res[pair[r --][1]] = a[i];//要放到原数组对应的位置上
            else res[pair[l ++][1]] = a[i];////要放到原数组对应的位置上
        }
        return res;
    }
}

 

871. 最低加油次数

　　描述：

　　　　

 

 

 　　　　

 

 

 　　思路：

　　　　

class Solution {
    public int minRefuelStops(int target, int startFuel, int[][] stations) {

        if(stations.length == 0)
            return startFuel>=target?0:-1;
        PriorityQueue<Integer>queue = new PriorityQueue<Integer>((o1,o2)->{
            return o2-o1;
        });
        int sum = startFuel;
        int ans = 0;
        for(int i = 0;i < stations.length;i++)
        {
            while(sum < stations[i][0])
            {
                Integer ii = queue.poll();
                if(ii == null)return -1;
                sum += ii;
                ans++;
            }
            queue.offer(stations[i][1]);
        }
        while(sum < target)
            {
                Integer ii = queue.poll();
                if(ii == null)return -1;
                sum += ii;
                ans++;
            }
        return ans;
        
        
    }
    
   
}

 

873. 最长的斐波那契子序列的长度

　　描述；
　　　　

 

 

 　　思路：dp[i][j]：表示以A[i],A[j]结尾的斐波那契数列的最大长度

　　　　　　　

 

 

 　　　　

for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            int diff = A[j] - A[i];
            if (intMap.count(diff)) {
                int index = intMap[diff];
                if (index < i) {
                    dp[i][j] = max(dp[i][j], dp[index][i] + 1);
                }
            }
            MAX = max(MAX, dp[i][j]);
        }
    }

875. 爱吃香蕉的珂珂

　　描述：

　　　　

 

 

 　　思路：二分。

877. 石子游戏

　　描述：
　　　　

 

 

 　　思路：动态规划。

880. 索引处的解码字符串

　　描述：

　　　　

 

 

 　　思路：栈。

881. 救生艇

　　描述：

　　　　

 

 

 　　思路：贪心。

　　　　

class Solution {
    public int numRescueBoats(int[] people, int limit) {
        Arrays.sort(people);
        int i = 0, j = people.length - 1;
        int ans = 0;

        while (i <= j) {
            ans++;
            if (people[i] + people[j] <= limit)
                i++;
            j--;
        }

        return ans;
    }
}

886. 可能的二分法

　　描述；

　　　　

 

 

 　　思路：深度优先，标记颜色。。类似于二部图的方法，。

887. 鸡蛋掉落

　　描述：

　　　　

 

 

 　　思路：

def superEggDrop(K: int, N: int):

    memo = dict()
    def dp(K, N) -> int:
        # base case
        if K == 1: return N
        if N == 0: return 0
        # 避免重复计算
        if (K, N) in memo:
            return memo[(K, N)]

        res = float('INF')
        # 穷举所有可能的选择
        for i in range(1, N + 1):
            res = min(res, 
                      max(
                            dp(K, N - i), 
                            dp(K - 1, i - 1)
                         ) + 1
                  )
        # 记入备忘录
        memo[(K, N)] = res
        return res

    return dp(K, N)

 

 

890. 查找和替换模式

　　描述：

　　　　

 

 

 　　思路：

class Solution {
    public List<String> findAndReplacePattern(String[] words, String pattern) {
        List<String> ans = new ArrayList();
        for (String word: words)
            if (match(word, pattern))
                ans.add(word);
        return ans;
    }

    public boolean match(String word, String pattern) {
        Map<Character, Character> m1 = new HashMap();
        Map<Character, Character> m2 = new HashMap();

        for (int i = 0; i < word.length(); ++i) {
            char w = word.charAt(i);
            char p = pattern.charAt(i);
            if (!m1.containsKey(w)) m1.put(w, p);
            if (!m2.containsKey(p)) m2.put(p, w);
            if (m1.get(w) != p || m2.get(p) != w)
                return false;
        }

        return true;
    }
}

 

894. 所有可能的满二叉树

　　描述：

　　　

 

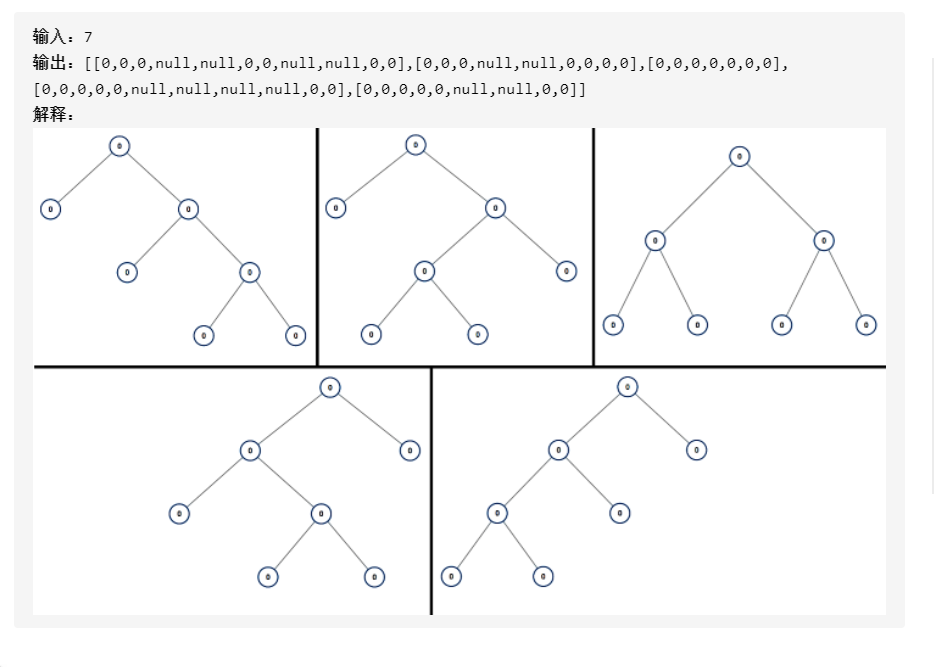
 　　思路：

　　　　Java 首先偶数是不能构成满二叉树的。 思路是把总node数分别左边，根，右边进行递归，如7个node可以分成1,1,5；3,1,5；5,1,1（左,根,右）。 5个node又可以分为1,1,3和3,1,1。 3个node又可以分为1,1,1。 1个node直接返回。

class Solution {
    private HashMap<Integer, List<TreeNode>> hm = null;
    public List<TreeNode> allPossibleFBT(int N) {
        List<TreeNode> rtn = new ArrayList<>();
        if(N % 2 == 0) return rtn;
        if(N == 1) {
            TreeNode root = new TreeNode(0);
            rtn.add(root);
            return rtn;
        }
        if(hm == null) hm = new HashMap<>();
        for(int i = 1; i < N; i += 2) {
            List<TreeNode> left = hm.getOrDefault(i, null);
            if(left == null) {
                left = allPossibleFBT(i);
                hm.put(i, left);
            }
            List<TreeNode> right = hm.getOrDefault(N - 1 - i, null);
            if(right == null) {
                right = allPossibleFBT(N - 1 - i);
                hm.put(N - 1 - i, right);
            }
            for(TreeNode l : left) {
                for(TreeNode r : right) {
                    TreeNode root = new TreeNode(0);
                    root.left = l;
                    root.right = r;
                    rtn.add(root);
                }
            }
        }
        return rtn;
    }
}