字符串匹配算法总结 (一对一匹配,多模式匹配)
1. 暴力算法 --bf算法
这是世界上最简单的算法了。
首先将匹配串和模式串左对齐,然后从左向右一个一个进行比较,如果不成功则模式串向右移动一个单位。
假设匹配串文本长度为n,模式串长度为m,最差的情况下,时间复杂度为O(m*n).
bf算法每次匹配不成功的时候,前面匹配成功的信息都被当作废物丢弃了,因此此方法速度最慢。
2. KMP算法
KMP算法的思想核心主要在Next数组。
在保证指针 i 不回溯的前提下,当匹配失败时,让模式串向右移动最大的距离;
并且可以在O(n+m)的时间数量级上完成对串的模式匹配操作;
在模式串和主串匹配时,各有一个指针指向当前进行匹配的字符(主串中是指针 i ,模式串中是指针 j ),在保证 i 指针不回溯的前提下,如果想实现功能,就只能让 j 指针回溯。
j 指针回溯的距离,就相当于模式串向右移动的距离。 j 指针回溯的越多,说明模式串向右移动的距离越长。
计算模式串向右移动的距离,就可以转化成:当某字符匹配失败后, j 指针回溯的位置。
对于一个给定的模式串,其中每个字符都有可能会遇到匹配失败,这时对应的 j 指针都需要回溯,具体回溯的位置其实还是由模式串本身来决定的,和主串没有关系。
模式串中的每个字符所对应 j 指针回溯的位置,可以通过算法得出,得到的结果相应地存储在一个数组中(默认数组名为 next )。
计算方法是:对于模式串中的某一字符来说,提取它前面的字符串,分别从字符串的两端查看连续相同的字符串的个数,在其基础上 +1 ,结果就是该字符对应的值。
例如:求模式串 “abcabac” 的 next 。前两个字符对应的 0 和 1 是固定的。
对于字符 ‘c’ 来说,提取字符串 “ab” ,‘a’ 和 ‘b’ 不相等,相同的字符串的个数为 0 ,0 + 1 = 1 ,所以 ‘c’ 对应的 next 值为 1 ;
第四个字符 ‘a’ ,提取 “abc” ,从首先 ‘a’ 和 ‘c’ 就不相等,相同的个数为 0 ,0 + 1 = 1 ,所以,‘a’ 对应的 next 值为 1 ;
第五个字符 ‘b’ ,提取 “abca” ,第一个 ‘a’ 和最后一个 ‘a’ 相同,相同个数为 1 ,1 + 1 = 2 ,所以,‘b’ 对应的 next 值为 2 ;
第六个字符 ‘a’ ,提取 “abcab” ,前两个字符 “ab” 和最后两个 “ab” 相同,相同个数为 2 ,2 + 1 = 3 ,所以,‘a’ 对应的 next 值为 3 ;
最后一个字符 ‘c’ ,提取 “abcaba” ,第一个字符 ‘a’ 和最后一个 ‘a’ 相同,相同个数为 1 ,1 + 1 = 2 ,所以 ‘c’ 对应的 next 值为 2 ;
所以,字符串 “abcabac” 对应的 next 数组中的值为(0,1,1,1,2,3,2)。
上边求值过程中,每次都需要判断字符串头部和尾部相同字符的个数,而在编写算法实现时,对于某个字符来说,可以借用前一个字符的判断结果,计算当前字符对应的 next 值。
具体的算法如下:
模式串T为(下标从1开始):“abcabac”
next数组(下标从1开始): 01
第三个字符 ‘c’ :由于前一个字符 ‘b’ 的 next 值为 1 ,取 T[1] = ‘a’ 和 ‘b’ 相比较,不相等,继续;由于 next[1] = 0,结束。 ‘c’ 对应的 next 值为1;(只要循环到 next[1] = 0 ,该字符的 next 值都为 1 )
模式串T为: “abcabac”
next数组(下标从1开始):011
第四个字符 ’a‘ :由于前一个字符 ‘c’ 的 next 值为 1 ,取 T[1] = ‘a’ 和 ‘c’ 相比较,不相等,继续;由于 next[1] = 0 ,结束。‘a’ 对应的 next 值为 1 ;
模式串T为: “abcabac”
next数组(下标从1开始):0111
第五个字符 ’b’ :由于前一个字符 ‘a’ 的 next 值为 1 ,取 T[1] = ‘a’ 和 ‘a’ 相比较,相等,结束。 ‘b’ 对应的 next 值为:1(前一个字符 ‘a’ 的 next 值) + 1 = 2 ;
模式串T为: “abcabac”
next数组(下标从1开始):01112
第六个字符 ‘a’ :由于前一个字符 ‘b’ 的 next 值为 2,取 T[2] = ‘b’ 和 ‘b’ 相比较,相等,所以结束。‘a’ 对应的 next 值为:2 (前一个字符 ‘b’ 的 next 值) + 1 = 3 ;
模式串T为: “abcabac”
next数组(下标从1开始):011123
第七个字符 ‘c’ :由于前一个字符 ‘a’ 的 next 值为 3 ,取 T[3] = ‘c’ 和 ‘a’ 相比较,不相等,继续;由于 next[3] = 1 ,所以取 T[1] = ‘a’ 和 ‘a’ 比较,相等,结束。‘a’ 对应的 next 值为:1 ( next[3] 的值) + 1 = 2 ;
模式串T为: “abcabac”
next数组(下标从1开始):0111232
基于next的KMP算法的实现:
先看一下 KMP 算法运行流程(假设主串:ababcabcacbab,模式串:abcac)。
第一次匹配:

匹配失败,i 指针不动,j = 1(字符‘c’的next值);
第二次匹配:

相等,继续,直到:

匹配失败,i 不动,j = 2 ( j 指向的字符 ‘c’ 的 next 值);
第三次匹配:

相等,i 和 j 后移,最终匹配成功。
3. horspool算法
Horspool是后缀搜索,也就是搜索已读入文本中是否含有模式串的后缀;如果有,是多长,显然,当后缀长度等于模式串的长度时,我们就找到了一个匹配。
Horspool算法思想:模式串从右向左进行匹配。对于每个文本搜索窗口,将窗口内的最后一个字符(C)与模式串的最后一个字符进行比较。如果相等,则继续从后向前验证其他字符,直到完全相等或者某个字符不匹配。然后,无论匹配与否,都将根据在模式串的下一个出现位置将窗口向右移动。模式串与文本串口匹配时,模式串的整体挪动,是从左往右,但是,每次挪动后,从模式串的最后一个字符从右往左进行匹配。
下面我们来看一个实例:
假设匹配串和模式串如下:
1.
匹配串:abcbcsdLinac-codecbcac
模式串:cbcac
首先从右向左进行匹配,c与c匹配成功,接着第二个字符b与a,匹配失败(失配位置为3)。于是,从模式串当前位置往左寻找匹配失败的那个字符,也即在模式串中寻找字符b上一次出现的位置(注意这里的“上一次”是指在模式串中从当前失配位置往左找到的第一个与失配位置相同的字符);结果我们在模式串中找到了字符b,其位置为1,那么就将模式串整体往右挪动,把刚才找到的字符b与之前与匹配串中失配的字符b对齐。总共移动了多少位呢?移动了(3-1)位。
2.
匹配串:abcbcsdLibac-codecbcac
模式串: cbcac
模式串整体挪动到b处对齐后,再从右向左开始匹配,此时发现其第一个需要匹配的字符d与c就匹配失败(失配位置为4),尼玛,坑爹啊!那接下来怎么办?当然是跟上一步的方法一样,在模式串中去找失配的那个字符d,如果在模式串中找到了d,将模式串平移,使其d字符与匹配串的d对齐。结果发现模式串中根本就没有字符d。那接下来怎么办?直接将模式串平移到刚才失配字符d后面的。这是因为模式串中没有字符d,那么就不可能在匹配串中的d及其前面的字符中匹配成功。这一次我们移动的位数是4-(-1)=5位。
3.
匹配串:abcbcsdLibac-codecbcac
模式串: cbcac
然后,又回到第1步的那种状态,从模式串的最后一个字符开始匹配,即c与c匹配,a与a匹配啊,然后发现b与c不匹配,从而我们在模式串中找b字符上一次出现的位置,发现其位置为1,移动模式串,将b字符与b字符对齐(如下图),这次我们移动的位数是2-1=1位。
4.
匹配串:abcbcsdLibac-codecbcac
模式串: cbcac
发现模式串中不含-,则模式串移动到-后面那个字符。
5.
匹配串:abcbcsdLibac-codecbcac
模式串: cbcac
这一次,在e与a处出现不匹配,而且e也没在模式串中出现过,那么模式串再右移到e的后面,这次移动的位数为:3-(-1)=4位。(为毛是减去-1?因为我们将模式串移动到失配字符的后面那个字符位置处去了,即相当将失配字符e与与模式串的第一个字符的前一个位置(-1处)对齐,懂否?)
6.
匹配串:abcbcsdLibac-codecbcac
模式串: cbcac
终于,在经历第五步的那次挪动后,我们匹配成功了,是不是感觉匹配速度特别快?
有了以上实例,我们现在来抽取其一般规则,以方便编码实现:
我们得到的规则只有一条,即:
字符串后移位数=失配字符位置-失配字符上一次出现的位置
如果失配字符根本就没有出现在模式串中,我们将“失配字符上一次出现的位置”的值视为-1。
4. sunnday算法
Sunday算法是从前往后匹配,在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符。
如果该字符没有在模式串中出现则直接跳过,即移动位数 = 模式串长度 + 1;
否则,其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。
下面举个例子说明下Sunday算法。假定现在要在主串”substring searching”中查找模式串”search”。
刚开始时,把模式串与文主串左边对齐:
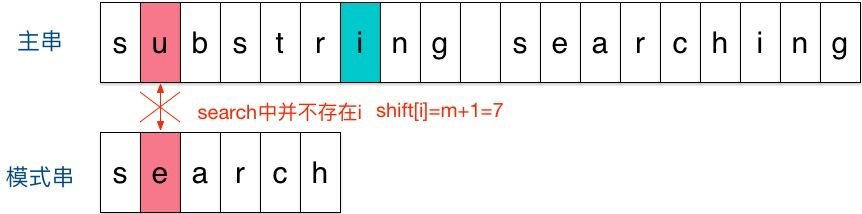
结果发现在第2个字符处发现不匹配,不匹配时关注主串中参加匹配的最末位字符的下一位字符,即标粗的字符 i,因为模式串search中并不存在i,所以模式串直接跳过一大片,向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7,从 i 之后的那个字符(即字符n)开始下一步的匹配,如下图:
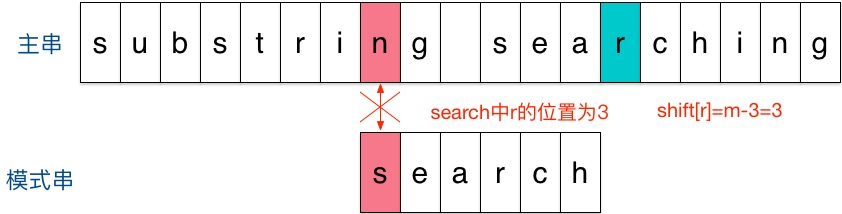
结果第一个字符就不匹配,再看主串中参加匹配的最末位字符的下一位字符,是’r’,它出现在模式串中的倒数第3位,于是把模式串向右移动3位(m - 3 = 6 - 3 = r 到模式串末尾的距离 + 1 = 2 + 1 =3),使两个’r’对齐,如下:
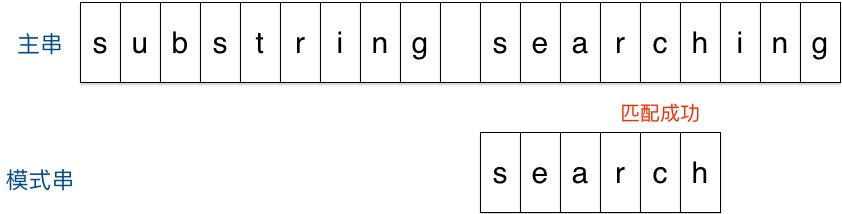
匹配成功。
回顾整个过程,我们只移动了两次模式串就找到了匹配位置,缘于Sunday算法每一步的移动量都比较大,效率很高。
5.RK算法
算法的预处理时间为O(m),但它的在最坏情况下的时间复杂度为O((2n-m+1)m),而平均复杂度接近O(m+n)
把文本每m个字符构成的字符段作为一个字段,和模式进行匹配检查。如果能对一个长度为m的字符串赋以一个Hash函数。那么显然只有那些与模式具有相同hash函数值的文本中的字符串才有可能与模式匹配,没有必要去考虑文本中所有长度为m的字段,因而大大提高了串匹配的速度。
将字符串的每一个字符看做一个数,那么这个字符串的就是一个数字数组,通过积分向量可以快速任意一个长度子字符串的向量和,可以把字符串的对应的字符数组的元素和看做这个字符串整体特征。
匹配串:aabsee sds
模式串 : ees
see向量和 == ees向量和,就对see和ees做逐个字符的比较,发现不匹配继续往下走。
匹配串:aabeessds
模式串 : ees
ees向量和 == ees向量和 ,就对ees和ees做逐个字符的比较,发现匹配OK。
6.BM算法
1.

假定字符串为"HERE IS A SIMPLE EXAMPLE",搜索词为"EXAMPLE"。
2.

首先,"字符串"与"搜索词"头部对齐,从尾部开始比较。
这是一个很聪明的想法,因为如果尾部字符不匹配,那么只要一次比较,就可以知道前7个字符(整体上)肯定不是要找的结果。
我们看到,"S"与"E"不匹配。这时,"S"就被称为"坏字符"(bad character),即不匹配的字符。我们还发现,"S"不包含在搜索词"EXAMPLE"之中,这意味着可以把搜索词直接移到"S"的后一位。
3.

依然从尾部开始比较,发现"P"与"E"不匹配,所以"P"是"坏字符"。但是,"P"包含在搜索词"EXAMPLE"之中。所以,将搜索词后移两位,两个"P"对齐。
4.
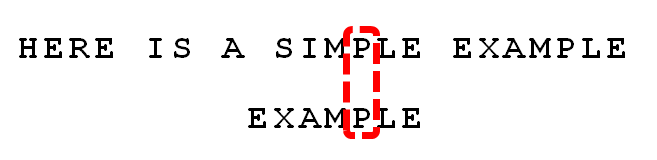
我们由此总结出"坏字符规则":
后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置
如果"坏字符"不包含在搜索词之中,则上一次出现位置为 -1。
以"P"为例,它作为"坏字符",出现在搜索词的第6位(从0开始编号),在搜索词中的上一次出现位置为4,所以后移 6 - 4 = 2位。再以前面第二步的"S"为例,它出现在第6位,上一次出现位置是 -1(即未出现),则整个搜索词后移 6 - (-1) = 7位。
5.

依然从尾部开始比较,"E"与"E"匹配。
6.
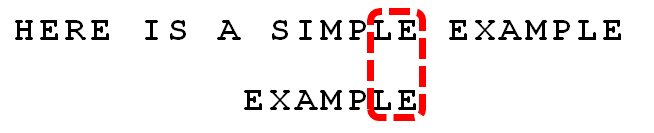
比较前面一位,"LE"与"LE"匹配。
7.
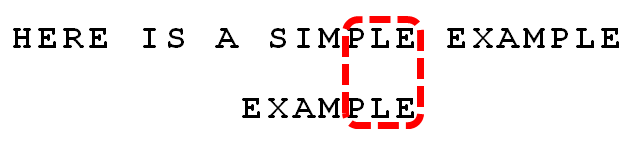
比较前面一位,"PLE"与"PLE"匹配。
8.

比较前面一位,"MPLE"与"MPLE"匹配。我们把这种情况称为"好后缀"(good suffix),即所有尾部匹配的字符串。注意,"MPLE"、"PLE"、"LE"、"E"都是好后缀。
9.
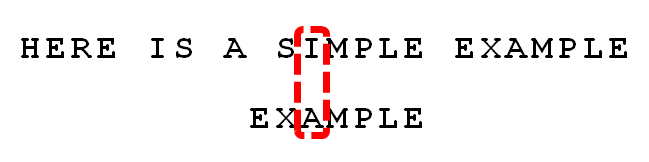
比较前一位,发现"I"与"A"不匹配。所以,"I"是"坏字符"。
10.
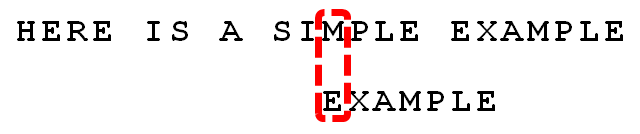
根据"坏字符规则",此时搜索词应该后移 2 - (-1)= 3 位。问题是,此时有没有更好的移法?
11.

我们知道,此时存在"好后缀"。所以,可以采用"好后缀规则":
后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置
举例来说,如果字符串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5(从0开始计算,取最后的"B"的值),在"搜索词中的上一次出现位置"是1(第一个"B"的位置),所以后移 5 - 1 = 4位,前一个"AB"移到后一个"AB"的位置。
再举一个例子,如果字符串"ABCDEF"的"EF"是好后缀,则"EF"的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 - (-1) = 6位,即整个字符串移到"F"的后一位。
这个规则有三个注意点:
(1)"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀,则它的位置以"F"为准,即5(从0开始计算)。
(2)如果"好后缀"在搜索词中只出现一次,则它的上一次出现位置为 -1。比如,"EF"在"ABCDEF"之中只出现一次,则它的上一次出现位置为-1(即未出现)。
(3)如果"好后缀"有多个,则除了最长的那个"好后缀",其他"好后缀"的上一次出现位置必须在头部。比如,假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B",请问这时"好后缀"的上一次出现位置是什么?回答是,此时采用的好后缀是"B",它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个"好后缀"只出现一次,则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB",即虚拟加入最前面的"DA"。
回到上文的这个例子。此时,所有的"好后缀"(MPLE、PLE、LE、E)之中,只有"E"在"EXAMPLE"还出现在头部,所以后移 6 - 0 = 6位。
12.
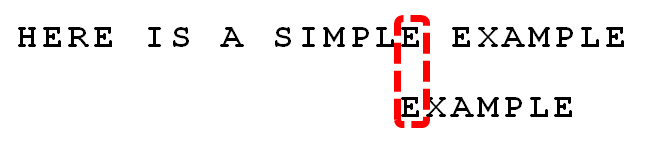
可以看到,"坏字符规则"只能移3位,"好后缀规则"可以移6位。所以,Boyer-Moore算法的基本思想是,每次后移这两个规则之中的较大值。
更巧妙的是,这两个规则的移动位数,只与搜索词有关,与原字符串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了。
13.
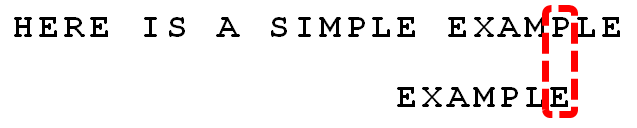
继续从尾部开始比较,"P"与"E"不匹配,因此"P"是"坏字符"。根据"坏字符规则",后移 6 - 4 = 2位。
14.

从尾部开始逐位比较,发现全部匹配,于是搜索结束。如果还要继续查找(即找出全部匹配),则根据"好后缀规则",后移 6 - 0 = 6位,即头部的"E"移到尾部的"E"的位置。
7.ac自动机
首先给定模式串"ash","shex","bcd","sha",然后我们根据模式串建立如下trie树:
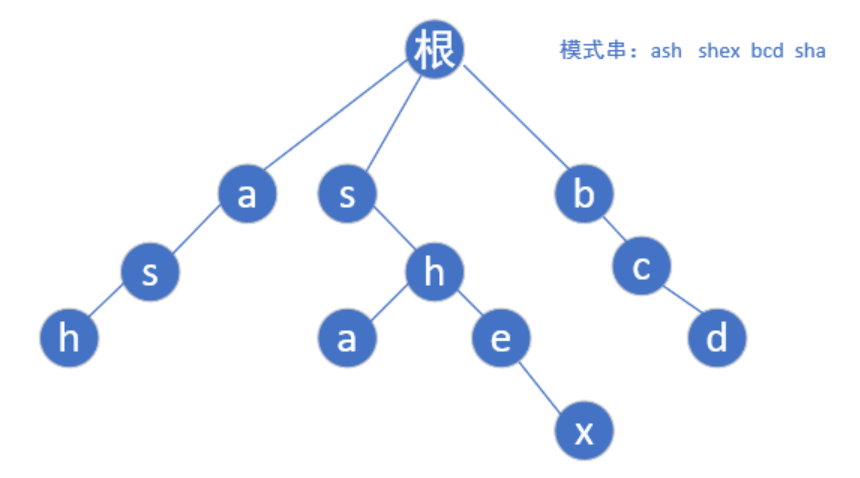
然后我们再了解下一步:
ac自动机,就是在tire树的基础上,增加一个fail指针,如果当前点匹配失败,则将指针转移到fail指针指向的地方,这样就不用回溯,而可以路匹配下去了.(当前模式串后缀和fail指针指向的模式串部分前缀相同,如abce和bcd,我们找到c发现下一个要找的不是e,就跳到bcd中的c处,看看此处的下一个字符(d)是不是应该找的那一个)
一般,fail指针的构建都是用bfs实现的
首先每个模式串的首字母肯定是指向根节点的(一个字母你瞎指什么指,指了也是头字母有什么用嘛)
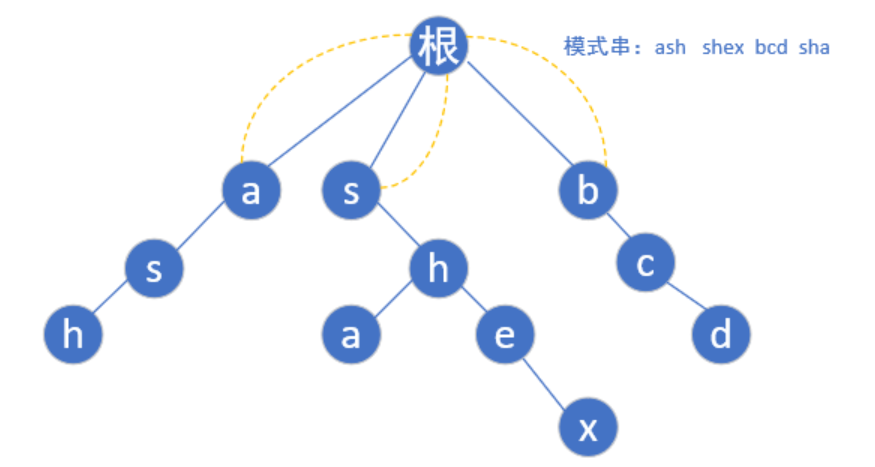
现在第一层bfs遍历完了,开始第二层
(根节点为第0层)第二层a的子节点为s,但是我们还是要从a-z遍历,如果不存在这个子节点我们就让他指向根节点(如下图红色的a)

当我们遍历到s的时候,由于存在s这个节点,我们就让他的fail指针指向他父亲节点(a)的fail指针指向的那个节点(根)的具有相同字母的子节点(第一层的s),也就是这样
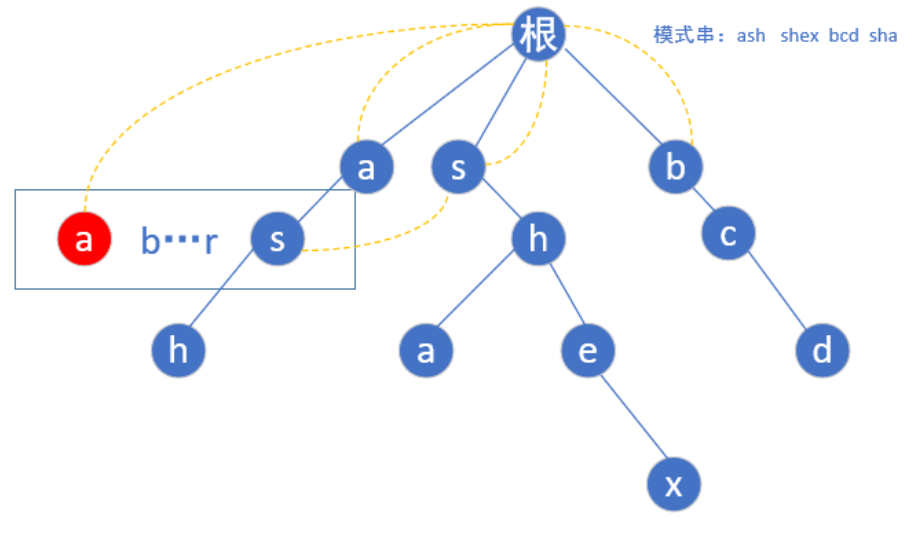
按照相同规律构建第二层后,到了第三层的h点,还是按照上面的规则,我们找到h的父亲节点(s)fail指针指向的那个位置(第一层的s)然后指向它所指向的相同字母根->s->h的这个链的h节点,如下图

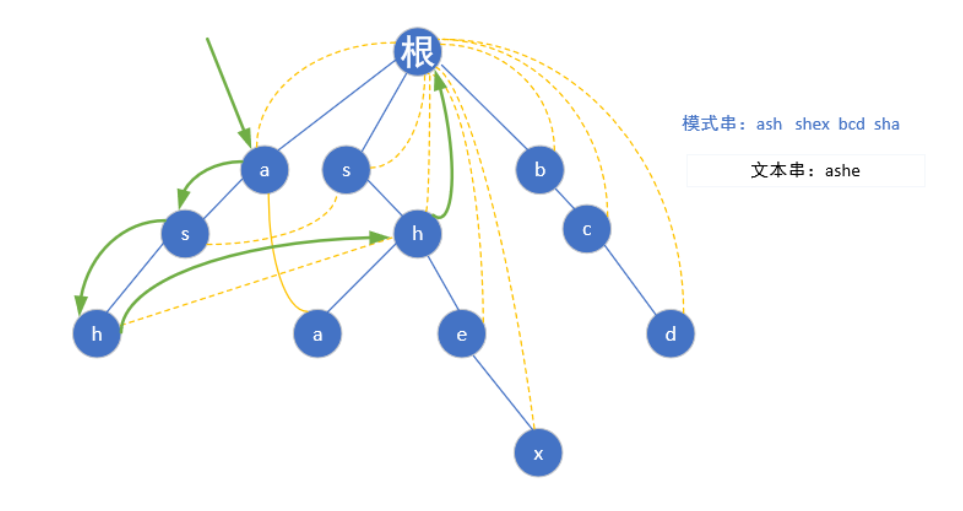
完全构造好后的树

然后匹配就很简单了,这里以ashe为例
我们先用ash匹配,到h了发现:诶这里ash是一个完整的模式串,好的ans++,然后找下一个e,可是ash后面没字母了啊,我们就跳到hfail指针指向的那个h继续找,还是没有?再跳,结果当前的h指向的是根节点,又从根节点找,然而还是没有找到e,程序END
过程如下图




 浙公网安备 33010602011771号
浙公网安备 33010602011771号