Codeforces Round #818 (Div. 2) D Madoka and The Corruption Scheme
Madoka and The Corruption Scheme#
组合数 + 思维 + 贪心
首先要思考一开始要如何摆放才是最优秀的
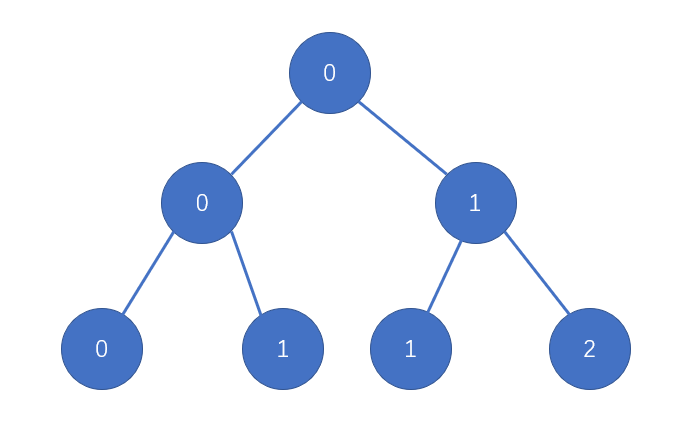
按照完全二叉树(根就是最后赢的那个),给所有的点赋予权值,代表需要转换多少条边,才能使得这个点的数字被选上
显然假设当前点的权值为 ,该点的其中一个节点权值必然为 (获胜),另一个点的权值必然是 (失败)
图中点的数字代表其权值,贪心地想,我们肯定要将小的数字尽可能的放置在权值低的点上(叶子),让别人尽可能的拿不到大的数字
通过观察发现,每一层的权值的种类与数量是杨辉三角的样子,所以如果能改 次,就相当于第 层的前 个值的和,都可以被调整为最终的胜利者
| 层 \ 点数量 \ 点权值 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 1 | |||
| 1 | 1 | 1 | ||
| 2 | 1 | 2 | 1 | |
| 3 | 1 | 3 | 3 | 1 |
第一列代表层数,第一行代表点权值, 代表第 层,权值为 的点个数
其实,因为每个点都会引申出一个本身权值,以及本身权值加一的点,显然就是杨辉三角了
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <string>
#include <queue>
#include <functional>
#include <map>
#include <set>
#include <cmath>
#include <cstring>
#include <deque>
#include <stack>
#include <ctime>
#include <cstdlib>
using namespace std;
typedef long long ll;
#define pii pair<int, int>
const ll maxn = 2e5 + 10;
const ll inf = 1e17 + 10;
const ll mod = 1e9 + 7;
ll fac[maxn], invfac[maxn];
ll qpow(ll x, ll n)
{
ll ans = 1;
while(n)
{
if(n & 1) ans = ans * x % mod;
n >>= 1;
x = x * x % mod;
}
return ans % mod;
}
ll cal(ll up, ll down)
{
if(up == down || up == 0) return 1;
ll ans = fac[down] * invfac[up] % mod;
return ans * invfac[down - up] % mod;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n, k;
cin >> n >> k;
fac[0] = 1;
for(int i=1; i<=n; i++) fac[i] = fac[i - 1] * i % mod;
invfac[n] = qpow(fac[n], mod - 2);
for(int i=n-1; i>=0; i--) invfac[i] = invfac[i + 1] * (i + 1) % mod;
ll ans = qpow(2, n);
if(k < n)
{
ans = 0;
for(int i=0; i<=k; i++)
ans += cal(i, n);
}
cout << ans % mod << endl;
return 0;
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 25岁的心里话
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 一起来玩mcp_server_sqlite,让AI帮你做增删改查!!
· 零经验选手,Compose 一天开发一款小游戏!