洛谷-P3195 玩具装箱
玩具装箱
dp + 斜率优化
\(dp[i]\) 表示前 \(i\) 个物品的最小代价,\(pre[i]\) 代表前 \(i\) 个物品的长度前缀和
设 \(x = pre[i] - pre[j] + i - j - 1 - L\),容易看出状态转移方程:
显然是一个 \(O(n^2)\) 的算法
可以设 \(x_i = pre[i] + i\),\(x_j = pre[j] + j + L + 1\)
有状态转移方程:
将平方拆开之后移向可以得到:
由上面的这个表达式可以将其化为 \(y = kx + b\) 的形式:
\(y = dp[j] + x_j^2\),\(k = 2x_i\),\(x = x_j\),\(b = dp[i] - x_i^2\)
因为我们要求 \(dp[i]\) 的最小值,也就是过点 \((x, y)\),斜率为 \(k\) 的直线的 截距 \(b\) 的最小值
显然点 \((x, y)\) 都与之前的 \(dp[j]\) 有关,直接暴力求解还是一个 \(O(n^2)\) 的算法,也就是相当于原算法抽象到坐标上的表示
根据观察,可以发现:
-
\(k\) 第随着 \(i\) 增大而逐渐增大的
-
\((x, y)\) 中的 \(x\) 也会随着 \(i\) 增大而增大
根据这两点,我们可以只维护这些离散点的下凸包,并且可以只用单调队列维护,因为截距最小的最优解只会经过下凸包的点
直接用单调队列维护,如图:队头就是下凸包右上角,队尾就是下凸包左下角,根据斜率从小到大(队尾到队头)来维护单调队列
假设点 \(p_1\) 和 \(p_2\) 的斜率表示为 \(f(p_1, p_2)\)
在单调队列中,对于截距最小的点 \(p_k\) 就有 \(f(p_{k-1}, p_k) < k\) 且 \(k \leq f(p_k, f_{k+1})\),图像上理解就是对于当前斜率,从最下边往上挪动,直到遇到一个点为止
考虑到斜率 \(k\) 是不断增大的,因此对于 \(p_k\) 后面的点(斜率更小的)都是没用的,他们都不可能是接下来的最优点
对于队头就维护一个下凸包就好了,对于当前点 \(p\) 和 队头点 \(p_j\),如果有 \(f(p_{j-1}, p_j) > f(p_{j-1}, p)\),则弹出队头的点,否则就加入当前点
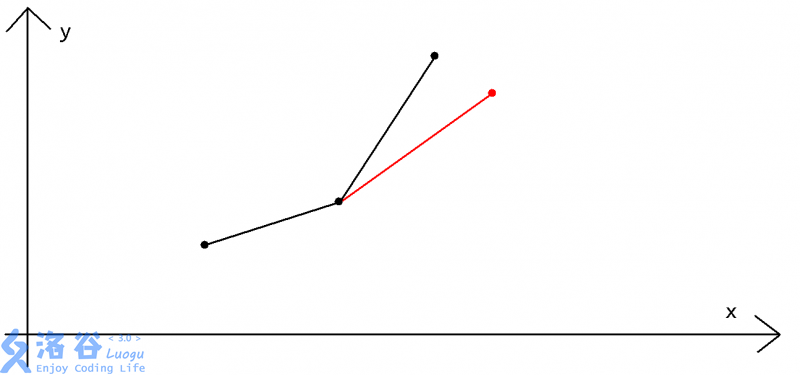
参考:
真心感觉这个很玄学
第一次写斜率优化的题,想了好久,不写一个详细的博客感觉对不起这段时间,但是又越写越像别人的博客,比较不喜欢画图,所以拿了两位大哥的图
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <deque>
using namespace std;
typedef long long ll;
#define pii pair<ll, ll>
const int maxn = 5e4 + 10;
ll dp[maxn], pre[maxn];
pii q[maxn];
double query(const pii& a, const pii& b)
{
double yy = b.second - a.second;
double xx = b.first - a.first;
return yy / xx;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll n, L;
cin >> n >> L;
for(int i=1; i<=n; i++)
{
cin >> pre[i];
pre[i] += pre[i-1];
}
int l = 0, r = -1;
for(int i=0; i<=n; i++)
{
ll xi = i + pre[i];
ll k = xi * 2;
while(l < r && query(q[l], q[l + 1]) < k) l++;
dp[i] = q[l].second - k * q[l].first + xi * xi;
ll xj = xi + L + 1;
pii now = {xj, dp[i] + xj * xj};
while(l < r && query(q[r - 1], q[r]) > query(q[r - 1], now)) r--;
q[++r] = now;
}
cout << dp[n] << endl;
return 0;
}



