数学知识

一、质数

1.试除法判断素数

 

2.筛素数

①埃氏筛 O（nloglogn）

 

for(int i=2;i<=n;i++){
    if(h[i]) continue;
    printf("%d ",i);
    for(int j=2;j*i<=n;j++) h[j*i]=1;
}

 

②线性筛 O（n）

每一个合数只会被自己最小的质因子筛掉，复杂度为O（n）

 

for(int i=2;i<=n;i++){
    if(!h[i]) primes[++cnt]=i;
    for(int j=1;j<=cnt&&primes[j]*i<=n;j++){
        h[primes[j]*i]=1;
        if(i%primes[j]==0) break;
    }
}

 

3.质因数分解

算数基本定理：任何一个大于1的自然数N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积N=P1^a1*P2^a2*P3^a3*......*Pn^an。其中P1,P2...Pn均为质数

“因为一个合数的因子一定在扫描到这个合数之前就从N中被除掉了，所以能整除N的一定是质数”（语出算法竞赛进阶指南）

 

for(int i=2;i<=sqrt(n);i++){
    if(n%i==0){//i是质数 
        primes[++cnt]=i;
        while(n%i==0) n/=i;
    }
}

 

 

二、约数

1.试除法求约数

 

2.约数个数

算数基本定理：任何一个大于1的自然数N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积N=P1^a1*P2^a2*P3^a3*......*Pn^an。其中P1,P2...Pn均为质数

若d为N的某个约数，则d=P1^b1*P2^b2*P3^b3*......*Pn^bn。其中0<=bi<=ai

所有bi不同取值即为约数个数，bi共有ai+1种取值

所以约数个数=（a1+1）（a2+1）...（an+1）

 

3.约数之和

约数之和=（P1^0+P1^1+...+P1^a1）*...*（Pn^0+Pn^1+...+Pn^an）

乘开就能理解了！

 

4.最大公约数-欧几里得算法

gcd（a，b）=gcd（b，a%b）

若a<b，a%b=a，显然gcd（a，b）=gcd（b，a）

若a>b，设a=q*b+r，对任意公约数d，d|a，d|q*b

所以d|a-q*b即d|r

int gcd(int a,int b){
    if(!b) return a;
    return gcd(b,a%b);
}

 

5.欧拉函数

互质：对任意a，b，若gcd（a，b）=1，则a与b互质

欧拉函数：φ（n）=1~n中与n互质的数的个数

由算数基本定理，N=P1^a1*P2^a2*P3^a3*......*Pn^an

①公式法求欧拉函数

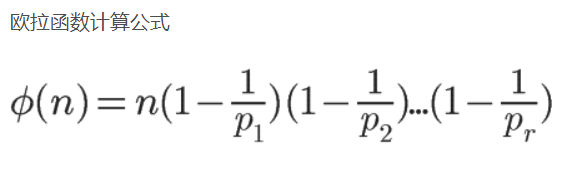
 （引于https://blog.csdn.net/bibohaohao/article/details/123697620）

容斥原理得公式

先从1~N中去除P1,P2...Pn的倍数

再加上Pi*Pj的倍数

再减去Pi*Pj*Pk的倍数

......以此类推，减去奇数个，加上偶数个

上述计算公式展开即为上述过程

②筛法求欧拉函数

（还没明白听懂了来补）

 

欧拉函数有什么用：欧拉定理

若a与n互质，则a^φ（n）≡1（mod n）

（这一部分等我再学一学来完善）

https://www.zhihu.com/question/274007455/answer/2282375359

 

三、同余

1.逆元

https://zhuanlan.zhihu.com/p/100587745

ab≡1（mod m）中a与b互为逆元

当m为质数时，由费马小定理得b^（m-1）≡1（mod m）

b^（m-2）*b≡1（mod m）

此时b^（m-2）与b互为逆元

2.扩展欧几里得