CIC滤波器
CIC滤波器是滑动平均滤波器的非常高效的迭代实现,只需要一个减法和一个加法,而滑动平均需要N-1个加法。
cic滤波器相当于一个梳状滤波器y(n)=x(n)-x(n-D),H(z)=1-z-D,和一个积分滤波器y(n)=x(n)+y(n-1),H(z)=(1-z-1)-1的级联,两个级联后y(n)=x(n)-x(n-D)+y(n-1),H(z)=(1-z-D)/(1-z-1),和求和表达式y(n)=x(n)+x(n-1)+x(n-2)...+x(n-D),H(z)=(1-z-D)/(1-z-1)一样.
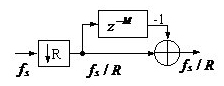
通常将comb部分放在低采样率步骤,可以减少存储器用于延时的Size,此乃精巧模式;an N-sample delay after decimation by R is equivalent to a D-sample delay before decimation by R。
问题
抽取后和抽取前的频域公式怎么变换?
x(n)=X(w)*ejwn,抽取后y(n)=x(Rn)=X(w)ejwRn=Y(w1)ejw1n;令w1=Rw,得到Y(w1)=X(w/R)。
抽取因子,差分因子改变对频域公式的影响?他们不一样对实际应用的影响?
抽取因子变化,对滤波器形状影响很小?同样的FIR滤波器可以用于变抽取因子的系统?
以上两个问题,可以回答为:H(z)=(1-z-RM)/(1-z-1),R倍抽取后变为H(z)=(1-z-M)/(1-z-1/R),系统的零点由分子决定,与R无关,因此R的变化不会改变滤波器的带宽,
梳妆滤波器和降采样颠倒后,差分因子变为N=D/R?
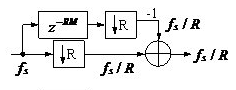 ->
-> 
CIC怎么降低硬件要求的?减少存储器,减小时钟
运算过程中位数的变化?
积分器有可能不溢出,满足两个条件?
CIC滤波器的FPGA表达(精巧模式):
process(rst,clk)
begin
if rst=1 then
y(n-1)=0;
k=0;
x(n)=0;
if rising(clk) then
x(n)=x(n)+xin;
k=k+1;
if k=3 then
k=0;
endif;
if k=0 then
y(n-1)=x(n);
y(n)=y(n-1);
yout=y(n)-y(n-1);
endif;
end process
CIC滤波器的FPGA表达(粗犷模式):
process(rst,clk)
begin
if rst=1 then
y(n-1)=0;
k=0;
if rising(clk) then
x(n)="0000"+xin;
x(n-1)=x(n);
x(n-2)=x(n-1);
x(n-3)=x(n-2);
xd4=x(n)-x(n-3);
y(n)=xd4+y(n-1);
k=k+1;
if k=0 then
yout=y(n);
endif;
if k=3 then
k=0;
endif;
end process



