散列算法与布隆过滤器

在Java Object以及HashCode简介中提到过Hash算法一文中对散列有一个初步的认识，一句话总结散列算法

对于任意输入长度的数据，经过Hash运算，使之能映射到指定的地址空间,后续针对此数据的查找演变为针对此特征值的查找过程

互联网下载文件常用的文件校验码是另一类Hash算法的典型应用,用于验证数据的完整性,来看一下apache tomcat的下载页面
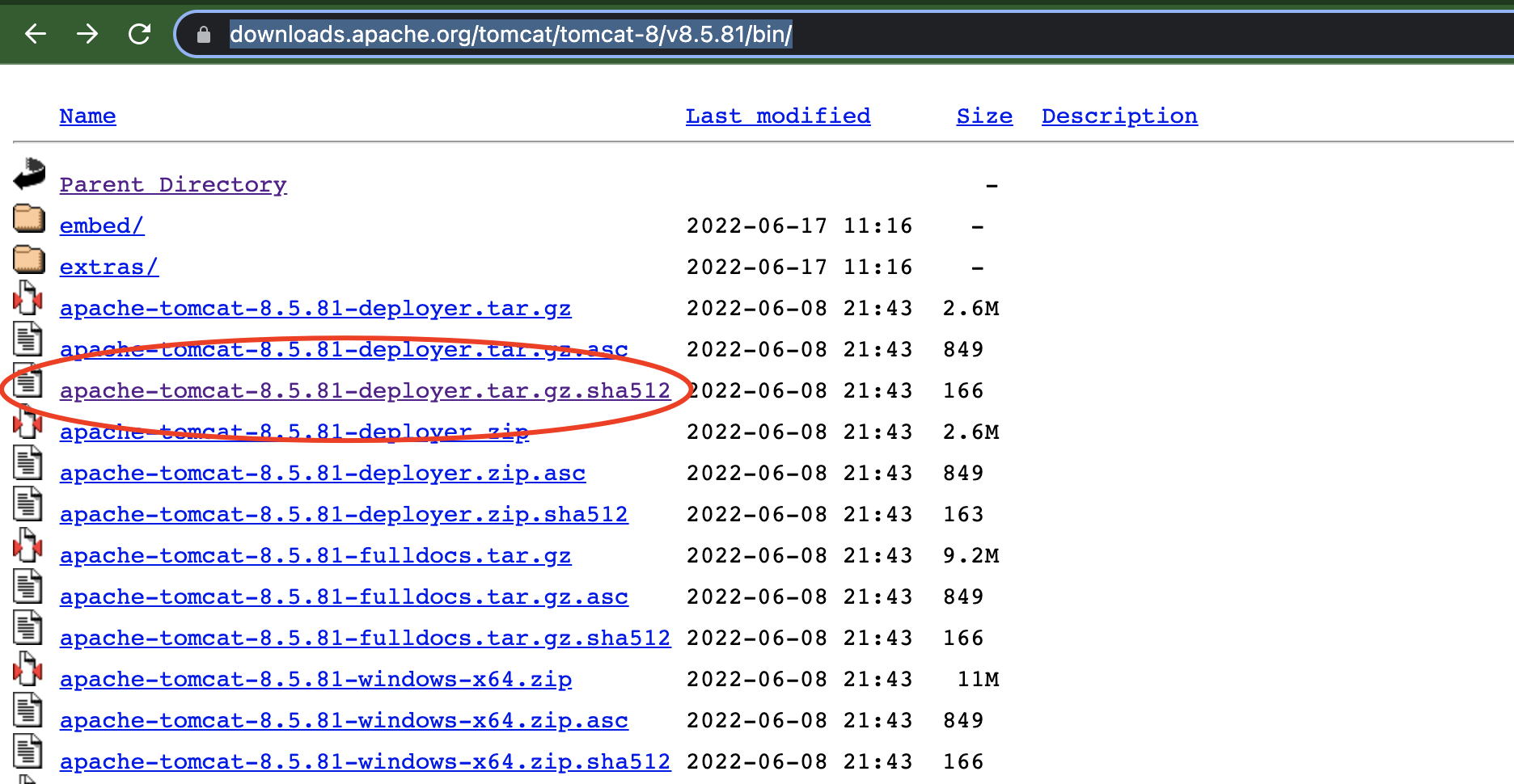
tomcat download

可以看到上述标红的部分即为文件的特征码/散列码/Hash值,可以看到文件后缀为sha512，代表使用sha512算法进行的散列，对应的文件内容为

4889f416a2c7548d6a94386496a788c7e611b5250df2ab4bddd7f3fba0e6989751983cc0914d32780b8bfe90da98d6f29024c8d60f69c560b8e8295db396e25a *apache-tomcat-8.5.81-deployer.tar.gz

对应的链接地址tomcat 8.5.81

下面简单介绍下互联网上几种散列算法

MD5 知名的散列算法，输出长度固定为16字节(128bit)，出现时间较早，诞生于上个世纪90年代，由Ron Rivest（RSA公司）提出，使用广泛
SHA1 与MD5同时代的算法，输出长度固定为20字节(160bit),由NSA提出
SHA2 通常包含SHA224,SHA256,SHA384,SHA512 ,SHA1的升级版，数字代表散列值的输出长度，通常长度越长代表越安全
SHA3 包含SHA3-224,SHA3-256,SHA3-384,SHA3-512,SHA的第三版，最新的标准

MD5/SHA1均已被攻破，不在被推荐使用，目前SHA2/SHA3暂被认为是安全的，可以放心使用

来看一下现实生活中的一个示例，下图演示法院在对被告作判决一个简短的示意图
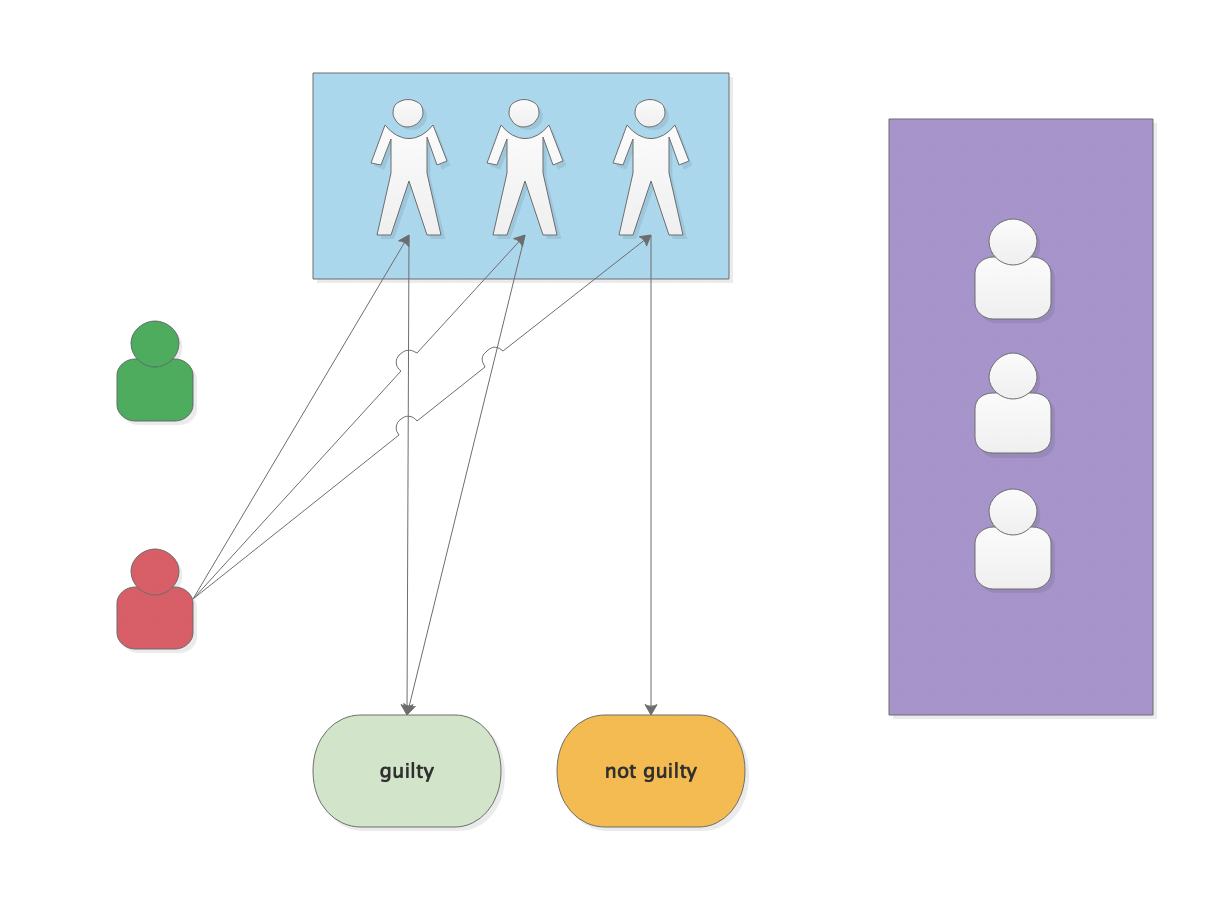
court_example

假定在对红色小人进行判罚的时候，三名证人基于自己了解的事件过程如实作答，基于此判定做出有罪/无罪判罚，在少数服从多数的情况下，假定认为投票数超过一半，那么法官便认为此人可以被定罪从而进行判罚(实际生活中的判罚过程比这个复杂的多的多)

Bloom Filter

上文介绍道散列算法可以对数据做完整形校验,散列值可以近似看作是数据的签名，它们一一对应，但是通常情况下数据是无限的，而签名是经过散列算法运算得到的固定输出的值，理论上来说他的地址空间有限，有限在理论上意味着有可能两个不一样的数据存在重复的可能，同样的在互联网的世界中，集群(实例数>=2)系统提供服务的可靠性(可用性)通常是远远大于单实例，在系统架构允许的情况下,可以选择增加集群中实例的数量，来达到提升系统可用性

Bloom Filter过滤器实质上是一个bit向量或者一个bit数组,通常情况下它长这样:
bloom_filter

bit 位为0代表数据不存在,bit 位为1 代表有数据，来看两个简单的数据写入示例:

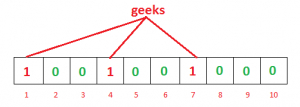
"geeks" 经过hash1("geeks")/hash2("geeks")/hash3("geeks") 运算后，生成三个散列值
将上述三个散列值分别与数组做取模运算,填充数组下标的值(将指定下标位置置为1)
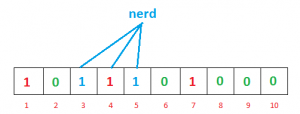
字符串"nerd"的写入过程同上述"geeks"，此处不在赘述

查询阶段，针对"geeks"，按照hash1("geeks")/hash2("geeks")/hash3("geeks") 计算后的值与数组长度做取模运算,三个bit都返回1，我们认为"geeks"在bloom filter中存在,针对字符串"foobar",经过hash1("geeks")/hash2("geeks")/hash3("geeks")运算后，假定返回上图中2/5/7这三个值，我们知道2这个位置为0，因此我们可以认为"foobar"字符串不存在bloom filter中，针对上述过程，我们可以发现

Bloom Filter需要多个散列函数参与数据集的散列运算
Bloom Filter不支持删除(通常意义上Bloom Filter底层数组数据可提前生成，有支持删除的Bloom Filter变种，大家可自行在互联网进行搜索)
Bloom Filter的向量/数字索引位只能保存2个值,通常代表两个状态
由于散列算法天然的特性(无限数据集->有限地址空间之间的映射)，散列冲突不可避免,因此Bloom Filter的得出数据的存在是一种假想意义上的存在,存在一定的误报率，只不过误报率通常情况下较低
Bloom Filter返回的不存在代表数据一定不存在
Bloom Filter的大小与输入的数据集长度无关

结合上述四点，可以看到Bloom Filter应用的场景非常适合于下述代码场景

public boolean exist(byte[] res){
    String hash1 = hashAlg1(res);
    String hash2 = hashAlg2(res);
    String hash3 = hashAlg3(res);
    if(BloomFilter.notExists(hash1,hash2,hash3)){
        // res
        return sendBackResNotExist();
    }else{
        // more action to confirm res exists in business system
        if(doMoreActionToConfirm(res)){
            addResToBloomFilter(res);
            return sendBackResExist();
        }else{
            return sendBackResNotExist();
        }
    }
}

回到上文中法院这一示例,红色小人(被告)扮演数据的角色,蓝色部分扮演的即是Bloom Filter，证人/证词/证物这一部分扮演的是散列/hash函数这一角色

Bloom Filter被大量应用于web 搜索引擎/反垃圾邮件过滤/缓存穿透等等应用场景，来看一个web 搜索引擎的示例:

互联网的web url链接的规模通常情况下都数以亿计,假定一家新型的搜索引擎公司需要用爬虫爬取整个互联网的url内容并进行索引，
初步假定要爬取的url的数量为100亿条，对于爬虫程序而言，为了降低无谓的工作量,已经被其他爬虫爬取过的页面内容，在近3天时间内无需再次抓取。

上述需求有三个关键点

数据量级较大(100亿),意味着传统的数据库存储方式已经不再适合
数据有效期为3天，三天后，为了保证数据的实时性，需要对已经抓取过的URL链接进行重新的抓取
每个URL仅需被抓取一次

针对场景1 ，假定Bloom Filter 散列函数为三个,那么需要生成的散列值的个数为3x100x10^9,占用的存储空间大小为3x100x10^8/(1024*1024*1024*8)，简约计算3x10x10^9/(10^9*8),约等于3.75GB的存储空间

针对场景2，Bloom Filter通常基于内存，3.75GB内存对于现今的服务器内存动不动上百G来讲，相当于九牛一毛，单台服务的内存就能存下如此多的数据，而且内存具有易失性的特性，借助于现今的各种缓存服务器，针对场景二也能很容易满足

针对场景三，结合上述关于Bloom Filter的介绍以及Bloom Filter的应用场景，不难看出场景三也很容易满足

Bloom Filter误判率

前文提到Bloom Filter对于已经存在的数据，Bloom Filter得出的结果是可能存在，实际上大家通过上述的介绍可以知道,只要散列冲突的概率越小,数组向量的长度越大,最终bit数组中产生的重复数据越小，亦即产生的误判率越低，以下几个方面可以降低Bloom Filter的误判率

散列冲突的概率可以选择合适的散列函数(算法)来优化数据的散列冲突
数组向量的绝对长度越大(空间越大),整个Bloom Filter被填满的速度越慢，产生的误判率亦即越低

实际应用上，散列算法的优化/可选择的散列函数均有一大票论文，而且对于技术的要求通常是比较高的，而数组的向量的绝对长度通常是比较好优化的一个手段/方向，基于业务体量,设计良好的分布式Bloom Filter可以支持横向扩展

附录:
文章图片链接来源:https://hackernoon.com/probabilistic-data-structures-bloom-filter-5374112a7832

posted @ 2022-06-27 20:58 dev_song 阅读(149) 评论(0) 编辑收藏举报

刷新页面返回顶部

dev_song

散列算法与布隆过滤器