硬件乘法专题-Booth-Wallace乘法
硬件乘法专题-Booth-Wallace乘法
本文提到的算法在 Github 开源:https://github.com/devindang/openip-hdl
该算法的设计文件也在此CPU设计中应用:https://github.com/devindang/dv-cpu-rv
有符号乘法
考虑一个8比特乘8比特的乘法,有符号乘法的结果可以表示为:
\([𝑋\cdot 𝑌]_{2𝑐} =−𝑋\cdot 𝑦_7 ⋅2^7 +𝑋\cdot 𝑦_6\cdot 2^6+\cdots+𝑋\cdot 𝑦_1\cdot 2^1 +𝑋\cdot 𝑦_0\cdot 2^0=[𝑋]_{2𝑐}\cdot (−𝑦_7\cdot 2^7+𝑦_6\cdot 2^6+\cdots+𝑦_1\cdot 2^1+𝑦_0\cdot 2^0)\)
其中,2c意为“2的补码”,在后续的表达式中,我将省略该符号,此处只讨论有符号乘法的运算。
这是最一般的二进制乘法的形式。假设两个数的位宽均为N,这种乘法需要计算的全位宽(N)加法的次数为N。
考虑以下例子,-13*6=-78,其中-13是被乘数(multiplicand),6是乘数(multiplier)。最后一个部分积是全0,在图中被省略。

下面的例子是,13*-6=-78,与上面的例子具有相同的结果。
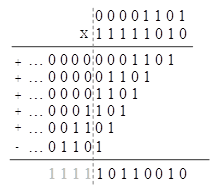
与无符号乘法不同的地方有:
1). 每个部分积均需符号扩展;
2). 最后一个部分积由减法运算产生,而非加法。
基2 Booth乘法
Booth乘法器对上式做变换,得到以下这种形式:
\([𝑋⋅𝑌]_{2𝑐} =[𝑋]_{2𝑐}\cdot(−𝑦_7\cdot 2^7+𝑦_6\cdot 2^6+\cdots +𝑦_1\cdot 2^1+𝑦_0\cdot 2^0)\)
\(=−𝑦_7\cdot 2^7+𝑦_6\cdot 2^6−𝑦_6\cdot 2^6+\cdots +𝑦_1\cdot 2^2−𝑦_1\cdot 2^1+𝑦_0\cdot 2^1−𝑦_0\cdot 2^0\)
\(=(𝑦_6 −𝑦_7)\cdot 2^7 +(𝑦_5 −𝑦_6)\cdot 2^6 +\cdots +(𝑦_0 −𝑦_1)\cdot 2^1 +(𝑦_{−1} −𝑦_0)\cdot 2^0\)
其中, \(𝑦_{−1} = 0\) . 通过变换, 有符号乘法运算的规律性被显现出来, 最后一个部分积的产生无需再乘以-1(减法). 这种算法称为基2 Booth算法,这是由于我们使用2比特产生了对应的1比特的“乘数”来产生部分积。
部分积的产生由 \(y_i y_{i-1}\) 共同确定:
| \(y_i\) | \(y_{i-1}\) | \(z_i\) | 注释 | z | neg |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 无需操作 | 0 | 0 |
| 0 | 1 | 1 | +X | 1 | 0 |
| 1 | 0 | -1 | -X (2的补码) | 1 | 1 |
| 1 | 1 | 0 | 无需操作 | 0 | 0 |
理论枯燥,考虑下面的例子,计算13x6:

注意灰色的"1"并非代表真实的进位,而是因为我省略了部分积中的部分符号位扩展(第二个部分积),计算结果一定是正数。
基4 Booth算法
让我们来讨论基 4 Booth 算法, 它是在现代 CPU 设计和 DSP 设计中最常用到的一种实现方式。
首先看基4 Booth算法中对于计算公式的变形:
\([𝑋\cdot 𝑌]_{2𝑐} =(𝑦_5 +𝑦_6 −2𝑦_7)\cdot 2^6 +(𝑦_3 +𝑦_4 −2𝑦_5)\cdot 2^4 +\cdots+(𝑦_{−1} +𝑦_0 −2𝑦_1)⋅2^0\)
Radix-4 Booth 算法不是将 2 个部分积划分到一起,而是将每 3 个部分积划分到一起,并每 2 位执行求和,或者说,乘数移位 2 位。 基4意味着,它将乘数设置为一组数字 0-3,而不仅仅是 0,1(基本阵列乘法,或基2 Booth 算法)。 这会将部分积的数量减少一半,因为您一次乘以两个二进制位。 然而,它需要乘以3,这是困难的。 (乘以 0、1 或 2 是微不足道的,因为它们只涉及简单的移,但是乘 3 是困难的)为了避免乘以 3,我们将 Booth 数字集重新编码为 2, 1, 0, ‐1 和‐2。
| \(y_{i+1}\) | \(y_i\) | \(y_{i-1}\) | \(z_i\) | 注释 | z0 | z1 | neg |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 无需操作 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | +X | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | +X | 1 | 0 | 0 |
| 0 | 1 | 1 | 2 | +2X | 0 | 1 | 0 |
| 1 | 0 | 0 | -2 | -2X (2的补码) | 0 | 1 | 1 |
| 1 | 0 | 1 | -1 | -X (2的补码) | 1 | 0 | 1 |
| 1 | 1 | 0 | -1 | -X (2的补码) | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 无需操作 | 0 | 0 | 0 |
z0, z1, neg 是在本设计中使用到的信号,其中z0意味着需要做1比特的移位,z1意味着需要做2比特的移位,neg意味着需要做减法运算(比特取反再+1)
z0, z1, neg 的产生很容易,可以通过简单的组合逻辑来实现,最简单的方式是从真值表来推断,其中:
\(z0=y_i \oplus y_{i-1}\)
\(z1 = (y_{i+1} \overline{y_i}) \overline{y_{i-1}} + (\overline{y_{i+1} y_i y_{i-1}})\)
\(neg=y_{i+1} \cdot \overline{(y_i \cdot y_{i-1})}\)
booth_encoder 模块用于产生这三个信号。当我们获得了这三个信号后,下一步操作是执行加法,减法,或移位操作来产生部分积送给 Wallace 树。为了实现这一逻辑, booth_selector 模块根据这三个信号来产生单比特的部分积。
单比特的部分积这样产生:
- 如果z1为1,则使用低1位的数字来产生部分积(等效于乘以2);
- 如果z0为1,则使用当前数字产生部分积;
- 如果neg为1,则仅对每一位取反,否则不做变换;
- 在每一级的N个比特部分积产生完成后,加上neg作为最终部分积。
下面我们看一个例子,这个例子是 13x6=78:
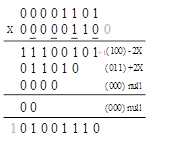
第一步:给乘数尾部添0,得到 00000110(0);
第二步:对100进行Booth编码,图中,每一个yi均使用下划线标示出了,100意味着-2X,z0=0, z1=1, neg=1;
第三步:产生第一个部分积,被乘数需要左移移位,换句话说,当前比特的部分积使用低1位的数字(这也是在本设计中实现的方法),得到00011010,因为neg是1,所以所有比特需要反转,得到11100101,同时需要加上1(也就是neg的值),neg的值被存入了一个叫做n的寄存器中,送往一个行波进位加法器来产生最终的部分积。
RCA #(65) u_rca(
.a (pp[u]),
.b ({64'd0,n[u]}),
.cin (1'b0),
.sum (pp2c[u]),
.cout ()
);
第四步:检查加下来的3比特,011意味着+2X,无需做2的补码变换。
第五步:继续操作,接下来两个部分乘数由000和000产生,意味着无需操作。
第六步,将所有部分积加起来,得到01001110(78).
你应当注意到了 0000 和 00 之间的实线,我们会在下一节讨论,这是与 Wallace 树相关的。
Booth编码将总的加法操作次数从N减少到了N/2,一半的加法运算被简单的移位和NOP(无操作)给替代了。
Wallace 树
回到上一节中的示例,实线是为 Wallace 树乘法放置的。 Wallace树将每3个Booth算法的部分积作为输入,并为下一阶段输出2个结果。下图示出了一种32位Wallace树,继续以这个例子为例,11100101被发送到最右边的CSA,同样,01101000和00000000(第三个部分积)、00000000(实线下的第四个部分积) 被送到右侧第 2 个 CSA 单元。
CSA单元:
Carray Save Adder,进位保留加法器,这是Wallace树的基本结构,他不产生进位结果,而是将每一位的进位直接输出,例如我们做一个64+64的加法,如果是行波进位加法器(RCA, Ripple Carry Adder),每一比特产生的进位都需要传递给下一位,从而至少64个加法器周期的延迟是必须的。而如果采用CSA,每一位的进位都直接输出,仅仅有一个加法器周期的延迟。这对时序是非常友好的。
Wallace树的结构可以通过下面的表进行推理,假设所有的操作数都是经过booth编码后的。
| 级数 | 独立输入 | 保留 | 输入 | 输出 |
|---|---|---|---|---|
| 0 | 0 | 2 | 10*3 | 10 *2 |
| 1 | 1 | 1 | 7*3 | 7 *2 |
| 2 | 1 | 0 | 5*3 | 5 *2 |
| 3 | 0 | 1 | 3*3 | 3 *2 |
| 4 | 0 | 1 | 2*3 | 2 *2 |
| 5 | 0 | 2 | 1*3 | 1 *2 |
| 6 | 1 | 1 | 1*3 | 1 *2 |
| 7 | 1 | 0 | 1*3 | 1 *2 |
用于乘法运算的 Wallace 树的基本加法器单元有 3 个输入 a、b、cin 和 2 个输出 sum、cout。 它使用 CSA(进位保留加法器)而不是 RCA(行波进位加法器),其中保存进位以供进一步加法,而不是行波到较高位,从而节省了延迟。
对于 stage 0,总输入个数32,有30个被送入10个CSA,剩下两个进行保留,在后面的CSA中进行运算;
对于 stage 1,总输入个数包括2个保留的内容,以及102个上一级的输出,共22个,因此有21个参与运算,使用2个保留的部分积中的1个作为独立输入,此时保留2个,共73个被送入CSA。
以此类推,可以画出下面的 Wallace 树。
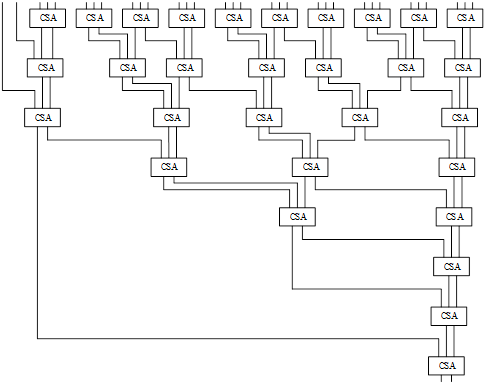
可以在适当的地方插入寄存器使得整个乘法器进行流水计算,比如在第二级,第五级,第八级插入寄存器,为Booth编码提供一定的建立时间裕量,如果时序不满足,可以增大流水线级数。
写在后面
完整的代码均在 Github 开源,包括完整的 testbench 文件,以及 modelsim 或者 vcs+verdi 的脚本,您可以一键运行仿真来学习 booth-wallace 算法,为中国的芯片行业以及开源事业贡献一份绵薄的力量!
参考资料
[1] 胡伟武. 计算机体系结构基础. 第3版, 机械工业出版社, 2021. Link


 浙公网安备 33010602011771号
浙公网安备 33010602011771号