硬件除法专题-SRT除法

本文提到的算法在 Github 开源：https://github.com/devindang/openip-hdl
该算法的设计文件也在此CPU设计中应用：https://github.com/devindang/dv-cpu-rv

概述

计算机中使用的硬件除法主要分为两大类：慢速除法和快速除法。

慢速除法在每次循环中只产生商和余数的一位，这类算法例如：恢复除法，非恢复除法，SRT除法。

而快速除法在每次循环中可能产生商或者余数的多位，例如：Newron-Raphson除法，Goldschmidt除法。

一些处理器及其使用的算法如下^[1]：

Processor	Division Algorithm	Connectivity
DEC 21164 Alpha AXP	SRT	Adder-Coupled
Hal Sparc64	SRT	Independent
HP PA7200	SRT	Independent
HP PA8000	SRT	Multiplier-accumulate-c/p
IBM RS/6000 Power2	Newton-Raphson	Integrated
Intel Pentium	SRT	Adder-coupled
Intel Pentium Pro	SRT	Independent
Mips R8000	Multiplicative	Integrated
Mips R10000	SRT	Multiplier-coupled
PowerPc 604	SRT	Integrated
PowerPc 620	SRT	Integrated
Sun SuperSparc	Goldschmidt	Multiplier-integrated
Sun UltraSparc	SRT	Independent

下面的讨论以 \(N/D=(Q,R)\) 为准，其中

N = numerator (dividend)，分子，被除数
D = denominator (divisor)，分母，除数
Q = quotient，商
R = Remainder，余数

循环相减

下面给出循环相减的伪代码，来自维基百科^[2]：

R := N
Q := 0
while R ≥ D do
  R := R − D
  Q := Q + 1
end
return (Q,R)

长除法（纸笔算法）

也叫，Paper-Pencil Division，伪代码如下：

if D = 0 then error(DivisionByZeroException) end
Q := 0                  -- Initialize quotient and remainder to zero
R := 0                     
for i := n − 1 .. 0 do  -- Where n is number of bits in N
  R := R << 1           -- Left-shift R by 1 bit
  R(0) := N(i)          -- Set the least-significant bit of R equal to bit i of the numerator
  if R ≥ D then
    R := R − D
    Q(i) := 1
  end
end

慢速算法

慢速算法通过循环等式，对余数R进行迭代：

\(R_{j+1}=B\times R_j-q_{n-(j+1)}\times D\)

其中，

\(R_j\) 是第 j 个部分余数
B 是基，在基2算法中，为2
\(q_{n-(j+1)}\) 是商的第 \(n-(j+1)\) 位，例如第1次迭代（j=0）产生 \(q_{n-1}\) ，商的最高位
n 是商的位数
D 是除数

其中：

\(R=R_n, N=R_0\)

\(R=2R_{n-1}-q_0D=2R_{n-2}-2^1q_1D-q_0D=\cdots\)

\(= 2^nN-2^{n-1}q_{n-1}D-\cdots-2^1q_1D-q_0D\)

\(=2^nN-QD\)

注意，R 和 D 均须左移 n 位，在运算前，需要把 D 左移，得到结果时把 R 右移。

恢复除法

恢复除法在迭代过程中选择 \(q_i\) ，其数集是 {0,1}

R := N
D := D << n            -- R and D need twice the word width of N and Q
for i := n − 1 .. 0 do  -- For example 31..0 for 32 bits
  R := 2 * R − D          -- Trial subtraction from shifted value (multiplication by 2 is a shift in binary representation)
  if R >= 0 then
    q(i) := 1          -- Result-bit 1
  else
    q(i) := 0          -- Result-bit 0
    R := R + D         -- New partial remainder is (restored) shifted value
  end
end
-- Where: N = numerator, D = denominator, n = #bits, R = partial remainder, q(i) = bit #i of quotient

以 13/5 = (2,3) 为例，

0. R := N = 13 = 00001101, D := D << 4 = 01010000
1. i=3, R = 00011010 - 01010000, q(3)=0, R = 00011010 (restored)
2. i=2, R = 00110100 - 01010000, q(2)=0, R = 00110100 (restored)
3. i=1, R = 01101000 - 01010000, q(1)=1
4. i=0, R = 00110000 - 01010000, q(0)=0, R = 00110000 => R=0011=3, Q=0010=2

非恢复除法

非恢复除法使用数集 {-1,1}，计算过程中额外的恢复运算。在这种算法下，每一位数字的基是 {-1,1} 而非 {0,1}，例如 \(-3=(-1)(1)(1)(-1)\)。

R := N
D := D << n            -- R and D need twice the word width of N and Q
for i = n − 1 .. 0 do  -- for example 31..0 for 32 bits
  if R >= 0 then
    q(i) := +1
    R := 2 * R − D
  else
    q(i) := −1
    R := 2 * R + D
  end if
end
-- Note: N=numerator, D=denominator, n=#bits, R=partial remainder, q(i)=bit #i of quotient.

由于得到的结果是非标准形式，因此需要在最后一步进行转换，转换方法如下：

Start: \(Q=111{\bar {1}}1{\bar {1}}1{\bar {1}}\)
Form the positive term: \(P=11101010\),
Mask the negative term*: \(M=00010101\)
Subtract: P-M: \(Q=11010101\)
*.( Signed binary notation with one's complement without two's complement)

这样最终算得的余数 R 介于 -D 到 D，例如 5/2=3R-1，如果要得到正数的余数，在转换之后执行以下步骤：

if R < 0 then
  Q := Q − 1
  R := R + D  -- Needed only if the remainder is of interest.
end if

SRT 除法

SRT 除法与非恢复除法类似，但它使用基于被除数和除数的查找表来确定每个商位。它和非恢复除法最显著的区别是，商使用了冗余表示。例如，在实现基 4 SRT 除法时，每个商位都是从五种可能性中选择的：{ −2, −1, 0, +1, +2 }。因此，商数的选择不必是完美的；后面的商数字可以纠正轻微的错误。（例如，商数字对 (0, +2) 和 (1, −2) 是等价的，因为 0×4+2 = 1×4−2。），这种冗余度允许仅使用少数几个被除数和除数的 MSB 数字来选择商位的数字，而不需要全位宽的减法。这种简化方法允许使用大于 2 的基数。

与非恢复除法一样，最后的步骤是最终的全位宽减法以解析最后一个商位，并将商转换为标准二进制形式。

SRT除法相比与非恢复除法不同点如下：

对 divisor 进行归一化，简化运算流程，缩小硬件实现面积，在SRT的第一步进行；
商位的选择使用冗余表示，允许仅使用少数几位来选择，无需使用全位宽的减法，这一过程通常由 QDS (quotient digit selection) 查找表实现；
由于使用冗余表示，需要对结果进行转换，通常使用on-the-fly conversion进行实时的转换，而不用浪费额外的时钟周期;
divisor 归一化会对计算得到的 quotient 和remainder 值造成影响，同时 remainder 可能是负数，需要进一步处理。

这些变化您将在后续的阐述中得到更为详尽的认识。

基2-SRT除法

基2-SRT除法中，数集为 \(\{\overline{1},0,1\}\)，迭代公式为 \(R_{j+1}=2\times R_j-q_i\times D\)；

基本步骤如下：

divisor 归一化：将 divisor 归一化至 \([1/2,1)\)，同时记录移位的个数 m，将dividend归一化至\((x,1/2)\), 同时记录移位个数n；
商位选择：根据“剩余余数”(部分余数)，做简单的移位，然后与 1/2 做对比选择商位 (非恢复除法中是与 D 做对比，SRT 算法将 D 归一化，简化了这一流程)，在基2-SRT中，QDS 查找表比较简单，可以直接做判断实现；
迭代计算：根据选择的商位对余数做迭代运算，总的迭代次数为m-n；
实时转换 (on-the-fly conversion)：根据实时转换算法，对 Remainder 和 Quotient 的值做实时转换，将迭代中使用的冗余形式转换为2进制补码形式；
后处理：根据移位个数 m 对商值以及余数进行调整，例如，对于无符号运算，同时如果余数为负数，需要对余数加上 D，同时商值减去 ulp (unit of least precision, 通常是1)。

这里不再提供伪代码，一来是维基百科上没有，不能保证权威性，二来是过程比较复杂，不能用简单的数值运算表示。

在SRT算法中，第一步是归一化除数和被除数，这加速了循环的过程，总的迭代次数也在这一步中被确定。

让我们看一个例子，计算11/3=(3,2)，除数和被除数都是8比特，8'd11=00001011, 8'd3=00000011.

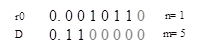
被除数11有4个前导0，而除数有6个前导0，我们将除数移位5比特得到0.110000，将被除数移位1比特得到0.0010110. 总的迭代次数是5-1=4。也就是除数的移位数减去被除数的移位数。如果除数的移位数小于被除数的移位数，这意味着被除数小于除数，也就不需要进行迭代了。

但是这样的迭代公式有一个缺点，每次确定商位的时候，使用 \(2_{r-1}\) 和 D 作为对比，如果二者的位宽都比较大，硬件电路占用的面积会非常大。

归一化把 D 限制在 \([\frac{1}{2},1)\) 的范围内，每次仅需比较 D 和1/2，-1/2的大小，1/2是0.1xxx，-1/2是1.0xxx，这样仅需两比特就能确定商位的值，而不用再进行全位宽的比较。在某些情况下，例如被除数X大于1/2，移位的操作会占用原有符号位的位置，因此一共需要3个比特。

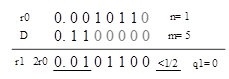
这是SRT算法商位选择的规则，它相比于非恢复除法，数集中多了 "0"，减少了加法和减法的次数。

\(q_i=\left\{\begin{array}{l} 1 & ,if&2r_{i-1}\geq D \\ 0 & ,if&-D \leq 2r_{r-1} < D \\ -1 &,if&2r_{i-1}< -D \end{array}\right.\)

对应的循环公式为：\(r_i=2r_{i-1}-q_i\cdot D\)

这里给出了以上例子的迭代步骤。

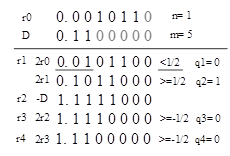
由于商的结果没有-1作为商位，所以也无需额外转换成标准形式。但是，注意余数是负数，这不是我们想要的，因此我们需要给r4加上D，并且给商值减去1：

不要忘记了给R右移m位，在这个例子中是5，我们因此得到了00000010(8'd2)作为最终的余数，00000011(8'd3)作为最终的商。

对于有符号的情况，商位的选择有所不同，但是遵循以下规则：

\(q_i=\left \{\begin{array}{l}0 & if|2r_{i-1}|<1/2\\ 1 & if|2r_{i-1}|\geq 1/2,r_{i-1}\;and\;D\;have\;the\;same\;sign\\ -1 & if|2r_{i-1}|\geq 1/2, r_{i-1}\;and\;D\;have\;opposite\;sign\end{array}\right.\)

基4-SRT除法

基4-SRT除法与基2-SRT除法相比，不同之处如下：

归一化的区别；
数集的变动，\(\{\overline{2},\overline{1},0,1,2\}\)通常是基4算法使用的数集，但不是唯一的；
商位的选择更加复杂，通常使用更复杂的 QDS 查找表实现；
On-the-fly 转换算法更加复杂；

基4的SRT算法使用每2比特进行迭代，迭代的次数同样由移位的比特来确定。使用m表示除数移位的比特，n表示被除数移位的比特，在基2算法中，总的迭代次数是m-n，但是在基4算法中，总的迭代次数是(m-n)/2，并且，m和n必须同样是偶数或者同样是奇数，否则会对迭代过程造成影响。

假设被除数是23，除数是5，这是一个无符号的例子，移位的情况如下：

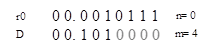
其中n=0，他和基2的情况不同，在基2中，我们会选择n=1作为移位数。同时，剩余余数还需要进行符号位扩展，如果上一个剩余余数比1/4大，也就是0.01xxxx，\(4r_{i-1}\)将会是1.xxxx，数字1掩盖了符号位。

基4-SRT算法的商位选择相比于基2算法来说更为复杂，一个很大的QDS表(Quotient Digit Selection)被用来确定商值。让我们来讨论选择的规则，同时构建QDS表用于RTL实现。

在基4-SRT算法中，我们选择的数集是{-2,-1,0,1,2}，这意味着冗余度是\(k=2/(4-1)=2/3\)，k是冗余度，它缩减了部分余数可允许的范围，部分余数被限定在以下范围内：\(-k\cdot D\leq r_i\leq k\cdot D\)。关于冗余度和冗余表示的概念，请参阅 Koren, Israel. "Computer arithmetic algorithms". CRC Press, 2018. 一书。

我们使用P来表示部分余数\(4r_{i-1}\)，则\(P=r_i+q\cdot D\)，因此

\[(-k+q)\cdot D\leq P \leq (k+q)\cdot D \]

画出P和D之间的关系，这个图被叫做PD图，x和y坐标均是QDS表的输入，商值是唯一输出。

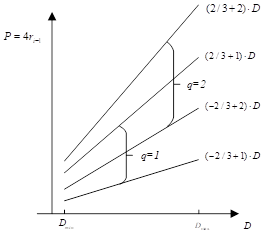
由此，我们可以构建以下的QDS表，多亏了归一化，我们可以仅仅检查少数几个比特来确定商值！

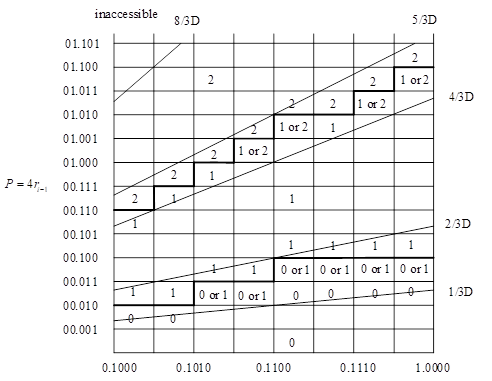
在这个PD图中，商值的选择与它左下角的坐标的是相关联的，例如，D=0.1010，P=00.011，我们应该选择1作为商值，然而如果D=0.1010，P=00.010，我们应该选择0。

图中标注了“0 or 1”或者“1 or 2”的意味着该处的商值可以选择0也可以选择1，粗实线是一种选择方案，这种选择方案允许更多的0和1，更少的2，简化了运算流程。

当我们得到了想要的商值之后，就可以继续迭代了，迭代过程如下：

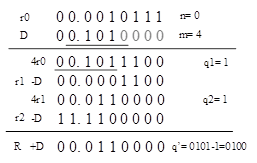
商值的选择由QDS表中选择，而非简单的与1/2做对比。在第一个循环中，P的索引是00.101，D的索引是0.1010，因此我们选择1作为商值，同时使用D去减4r0，得到r1。

把最后的商值转换为标准形式：

基4中的11是基2中的0101，这里没有负数项，无需做减法。

本节结束了？我们还没有谈论负数的情况。考虑23/-5=(-4,3)，

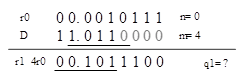
我们改怎么选择商值呢？首先，需要把D转换为正数（原码）的形式，0.1010，然后使用负数的QDS表进行查表。

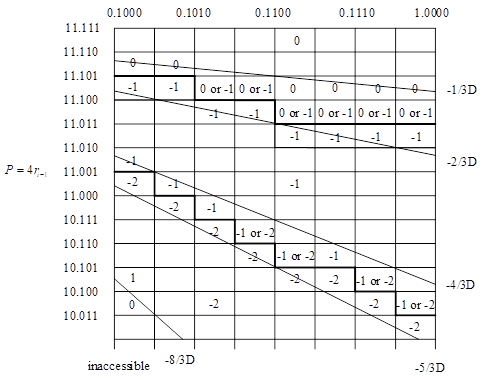
与正数的QDS表不同，我们不再选择左下角的点，而是左上角的点，与商值相关联，例如，如果D=0.1010, P=11.101，我们应该选择-1作为商值。在正数的情况下，我们选择了1.

以下的例子是23/-5=(-4，3),过程和无符号的SRT算法类似。

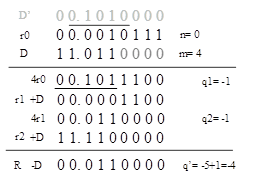
需要注意的是，因为除数是负数，在后处理过程中，q应该加上1，R应该减去D（负数）。

以下的例子是-23/5=(-5,2)：

注意，余数的符号没有明确的定义，例如，-29/-26，在Matlab中，得到-3作为余数，它保持余数和被除数具有相同的符号；而在python中，余数与除数的符号相同，在某些场合下，余数总是正的。在改实现中，余数总是正值，程序会给出的余数值是23，因为-26*2+23=-29.

On-the-fly转换^[3]

由于冗余数集存在负数，商的表示并非标准形式，我们需要把非标准形式的商在算法的最后一步转换为标准形式。但是它需要耗费额外的延迟以及芯片面积：对于减法操作，全位宽的进位加法器是必须的，如果使用行波进位加法器，延迟将会大到N，如果使用超前进位加法器，需要牺牲芯片的面积。

On-the-fly转换是为了获得实时的转换结果而设计的，它仅仅使用2个Flip-Flop和一些简单的组合逻辑就可以完成转换过程。

Q的实际值可以表示为以下形式：\(Q[j]=\sum_{i=1}^j q_i r^{-i}\)，更新公式为：\(Q[j+1]=Q[j]+q_{j+1}r^{-(j+1)}\)，其中，\(Q[j]\)是Q的真实值在第j次迭代的结果，\(q_i\)是商位，是冗余表示。由于\(q_{j+1}\)可以是负的：

\[Q[j+1]=\left \{ \begin{array}{l} Q[j]+q_{j+1}r^{-(j+1)} & ,\;if\;q_{j+1}\geq 0 \\ Q[j]-r^{-j}+(r-|q_{j+1}|)r^{-(j+1)}&,\;if\;q_{j+1}<0\end{array}\right. \]

该更新公式有一个缺点，需要做减法，进位的传播会使电路变得很慢，因此我们定义另一个寄存器\(QM[j]=Q[j]-r^{-j}\)，其中QM意思是Quotient of Minus。

\[Q[j+1]=\left\{\begin{array}{l} Q[j]+q_{j+1}r^{-(j+1)} & ,\;if\;q_{j+1}\geq 0 \\ QM[j]+(r-|q_{j+1}|)r^{-(j+1)}&,\;if\;q_{j+1}<0\end{array}\right. \]

减法操作可以被替换为对寄存器 QM 进行采样，QM可以通过以下公式进行更新：

\[QM[j+1]=\left\{\begin{array}{l} Q[j]+(q_{j+1}-1)r^{-(j+1)} & ,\;if\;q_{j+1}> 0 \\ QM[j]+(r-|(r-1)-q_{j+1}|)r^{-(j+1)}&,\;if\;q_{j+1}\leq 0\end{array}\right. \]

项\(r^{j+1}\)可以通过将\(q_{j+1}\)拼接到寄存器Q或者QM的后面来实现。因此，我们得到了On-the-fly转换方法的更新公式：

\[Q[j+1]=\left\{\begin{array}{l} \{Q[j],q_{j+1}\} & ,\;if\;q_{j+1}\geq 0 \\ \{QM[j],(r-|q_{j+1}|)\}&,\;if\;q_{j+1}<0\end{array}\right. \]

\[QM[j+1]=\left\{\begin{array}{l} \{Q[j],q_{j+1}-1\} & ,\;if\;q_{j+1}> 0 \\ \{QM[j],((r-1)-|q_{j+1}|)\}&,\;if\;q_{j+1}\leq0\end{array}\right. \]

它的硬件实现流程图由下图描述：

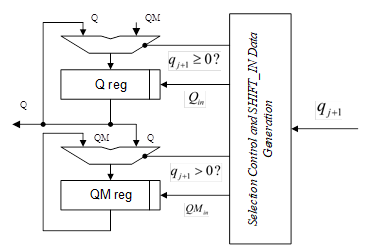
初始化条件为：

\[Q=QM=\left\{\begin{array}{l}all\;0s,\;if\;quotient\;positive \\ all\;1s,\;if\;quotient\;negative\end{array}\right. \]

我们可以简单的根据除数和被除数的符号来推断商的符号：如果被除数和除数具有相反的符号，我们就把Q和QM初始化为全1，否则就初始化为全0。

SHIFT_IN的数值产生（拼接的部分）可以简单的通过真值表来推断，对于基4的情况（基2的情况更简单）：

\[Q[j+1]=\left\{\begin{array}{l} \{Q[j],q\} & ,\;if\;q\geq 0 \\ \{QM[j],1'b1,q[0]\}&,\;if\;q<0\end{array}\right. \]

\[QM[j+1]=\left\{\begin{array}{l} \{Q[j],1'b0,q\} & ,\;if\;q\geq 0 \\ \{QM[j],\sim q\}&,\;if\;q<0\end{array}\right. \]

这里也给出了一个基2情况下转换的例子，它把1101(-1)00转换为1100100，也就是1101000-00000100。

\(j\)	\(q_j\)	\(Q[j]\)	\(QM[j]\)
0		0	0
1	1	0.1	0.0
2	1	0.11	0.10
3	0	0.110	0.101
4	1	0.1101	0.1100
5	-1	0.11001	0.11000
6	0	0.110010	0.110001
7	0	0.1100100	0.1100011

本文的内容大部分参考自^[4] Koren, Israel. "Computer arithmetic algorithms". 请以原书为准。

写在后面

完整的代码均在 Github 开源，包括完整的 testbench 文件，以及 modelsim 或者 vcs+verdi 的脚本，您可以一键运行仿真来学习 SRT 算法，为中国的芯片行业以及开源事业贡献一份绵薄的力量！

参考资料

https://userpages.umbc.edu/~squire/images/srt1.pdf ↩︎
https://en.wikipedia.org/wiki/Division_algorithm ↩︎
Ercegovac, and Lang. "On-the-fly conversion of redundant into conventional representations." IEEE Transactions on Computers 100.7 (1987): 895-897. ↩︎
Koren, Israel. "Computer arithmetic algorithms". CRC Press, 2018. ↩︎

posted @ 2023-08-16 11:22 devindd 阅读(2499) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

硬件除法专题-SRT除法

硬件除法专题-SRT除法

概述

循环相减

长除法（纸笔算法）

慢速算法

恢复除法

非恢复除法

SRT 除法

基2-SRT除法

基4-SRT除法

On-the-fly转换[3]

写在后面

参考资料

公告

On-the-fly转换^[3]