高斯信道下数字调制理论误码率

BER的理论计算

理论推导过程在这篇文章，感兴趣的可以看一下 知乎-理论误码率推导

BERtool

matlab的bertool可以很方便的绘制各种调制方式和各种信道下的理论误码率曲线。

在command输入bertool，就可以打开ber分析工具，如图1所示，可以指定各种信道和调制方式，调制阶数等等，点击plot就可以开始绘制。

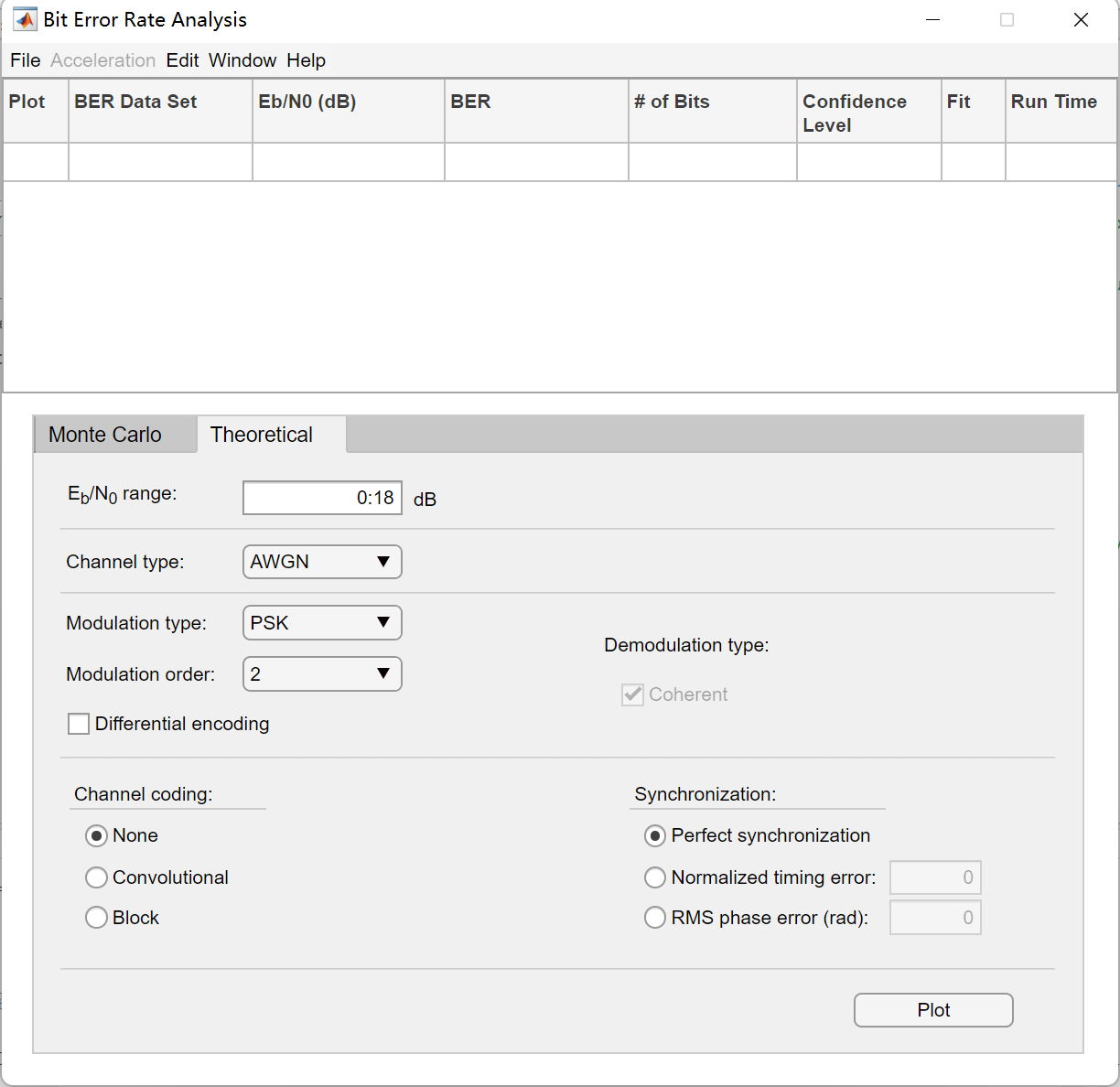
图1 ber分析工具

可以分别调整\(E_b/N_0\)的范围，信道类型，调制方式，调制阶数等等，注意横轴是\(E_b/N0\)，如果需要SNR的话，注意换算。换算方式如下：

matlab帮助中心AWGN Noise Level

绘制出来的BER曲线如图2所示，注意，点击上面的箭头可以启用编辑，此时可以复制曲线到自己的BER曲线上进行比较。

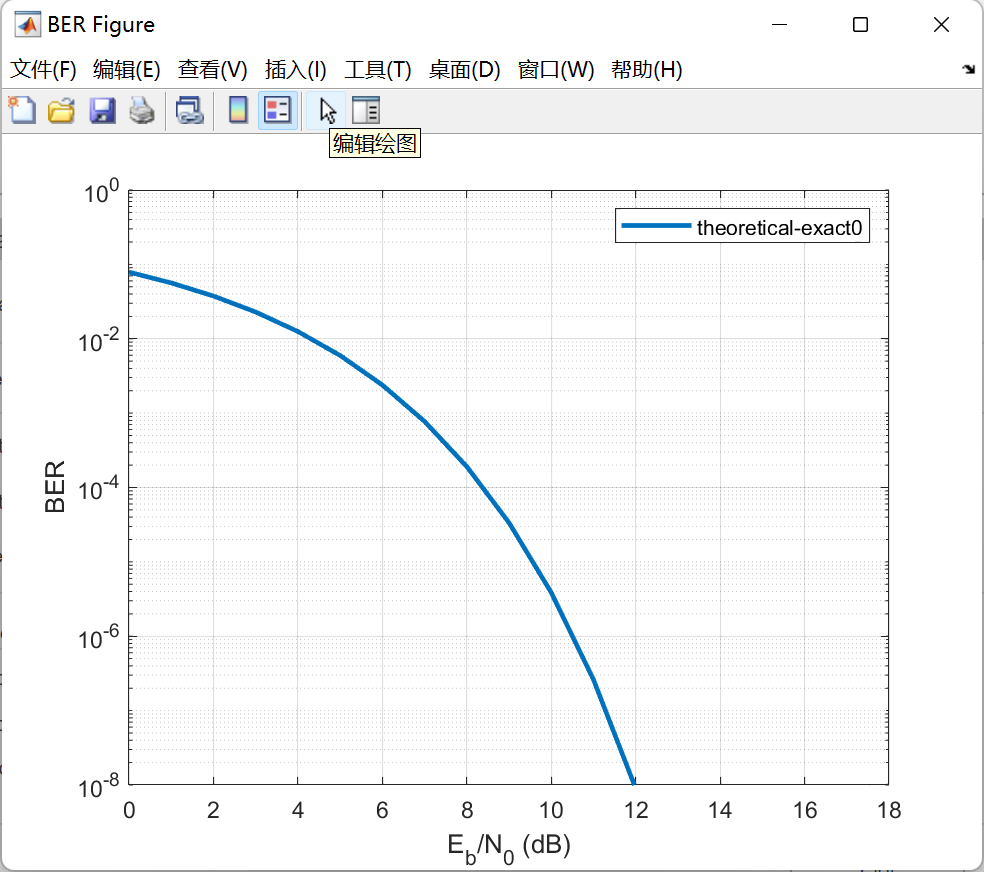
图2 高斯信道下BPSK的理论误码率

EsN0和EbN0的关系

这里复述一下，首先给出\(E_s/N_0\)和\(E_b/N_0\)的关系，其中\(E_s\)和\(E_b\)分别是每个符号和每个比特上的能量。显而易见：

\(E_s/N_0=E_b/N_0+10log_{10}(k)\)，其中\(k\)为每个符号上的信息比特数，对于BPSK，\(k=1\)，对于\(k=2\)，其他调制方式类似。

EsN0和SNR的关系

\(E_s/N_0(dB)=10log_{10}(T_{sym}/T_{samp})+SNR(dB)\)，对于复信号

\(E_s/N_0(dB)=10log_{10}(0.5T_{sym}/T_{samp})+SNR(dB)\)，对于实信号

EsN0和SNR关系的推导

对于复信号，

\(\begin{aligned} E_s/N_0(dB)&= 10log_{10}((S\cdot T_{sym})/(N/B_n))\\ &=10log_{10}((T_{sym}F_s)\cdot (S/N))\\ &= 10log_{10}(T_{sym}/T_{samp})+SNR(dB)\end{aligned}\)

其中，

• \(S\) = 输入信号功率
• \(N\) = 噪声功率
• \(B_n\) = 噪声带宽，=F_s=1/T_{samp}$
• \(F_s\) = 采样频率

如果是实信号，相同噪声功率情况下，占用的带宽是原来的0.5倍，因此换算出来的\(E_s/N_0\)会比复信号少\(3dB\)。

使用互补误差函数计理论误码率

高斯信道下，BPSK和QPSK的BER计算方式如下：

\[ber=\frac{1}{2}erfc(\sqrt\frac{E_b}{N_0}) \]

高斯信道下，QAM的BER计算方式如下：

\[ber=\frac{4(1-M^{-\frac{1}{2}})}{log_2M}Q(\sqrt{\frac{3log_2(M)}{M-1}\cdot\frac{E_b}{N_0}}) \]

对应的matlab代码放到这里，

function ber=ber_QAM(EbN0dB,M,AWGN_or_Rayleigh)
% Find ananlytical BER of Mary QAM in AWGN or Rayleigh channel
% EbN0dB = EbN0dB: Energy per bit-to-noise power[dB] for AWGN channel
%        = rdB: Average SNR(2*sigma Eb/N0)[dB] for Rayleigh channel
% M = Modulation order (Constellation size)  
% MIMO-OFDM Wireless Communications with MATLAB

sqM= sqrt(M); 
a= 2*(1-power(sqM,-1))/log2(sqM);
b= 6*log2(sqM)/(M-1);
if nargin<3
    AWGN_or_Rayleigh='AWGN';
end

if lower(AWGN_or_Rayleigh(1))=='a'
    ber = a*Q(sqrt(b*10.^(EbN0dB/10)));
else
    rn= b*10.^(EbN0dB/10)/2; 
    ber = 0.5*a*(1-sqrt(rn./(rn+1)));
end

end