功率谱估计技术概述

周期图法

一般而言，估计一个信号\(x(n)\)的功率谱密度的一种简单的方法是截取长度为\(L\)的一段样本，并作离散时间傅里叶变换（通常使用FFT完成）并适当地缩放结果的幅度平方。 这种估计方法称为周期图。

周期图法包含了下列二条假设：

  1. 认为随机序列是广义平稳且各态遍历的，可以用其一个样本x(n)中的一段来估计该随机序列的功率谱。这当然必然带来误差。

  2. 由于采用DFT，默认在时域是周期的，以及在频域是周期的。这种方法把随机序列样本x(n)看成是截得一段的周期延拓，这也就是周期图法这个名字的来历。

长度为\(L\)的信号\(x_L(n)\)的周期图法PSD估计为：

\(P_{xx}(f)=\frac{1}{LF_s}\left| \sum_{n=0}^{L-1}x_L(n)e^{-j2\pi fn/F_s}\right|^2\)

如果频域是离散的，则有

\(f_k=\frac{kF_s}{L},where,k=0,1,\cdots L-1\)

自相关法（Blackman-Tukey法）

BT法进行谱估计基于维纳-辛钦定理：

维纳-辛钦定理，又称维纳-辛钦-爱因斯坦定理或辛钦-柯尔莫哥洛夫定理。该定理指出：任意一个均值为常数的广义平稳随机过程的功率谱密度是其自相关函数的傅立叶变换。

\(P_X(f)=\left|\sum_{k=0}^{M-1}w_k r_k e^{-2\pi i fk}\right|\)

周期图法和BT法在历史上经历了一个此起彼落的过程，周期图法是一种古老的方法被广泛采用，1958年，维纳辛钦定理提出以后，BT法优于计算比周期图法简单而被普遍采用，1965年，FFT算法的提出，使得周期图法又被广泛运用至今[1]。

频谱泄露

在介绍修改的周期图法之前，先简要介绍一下频谱泄露现象。我们知道，傅里叶变换（FT，Fourier Transform）是对连续非周期的信号进行分析，这样的信号是不能被计算机处理的，计算机只能处理离散的信号，也就是说要对连续信号进行采样，得到离散信号；同时，由于原信号是非周期的，信号周期无限长，因此计算机只能截取其中的一段进行处理。截取的这一过程，等同于加了一个矩形窗。

举个例子，如图1所示，该信号频率为100Hz，其中，上面是1000个点的取样结果，下面是100个点的取样结果，采样频率1000Hz，这样，100个点的采样恰好可以包括完整的10个周期。此时做FFT，得到的频谱与信号本身的频谱一致。
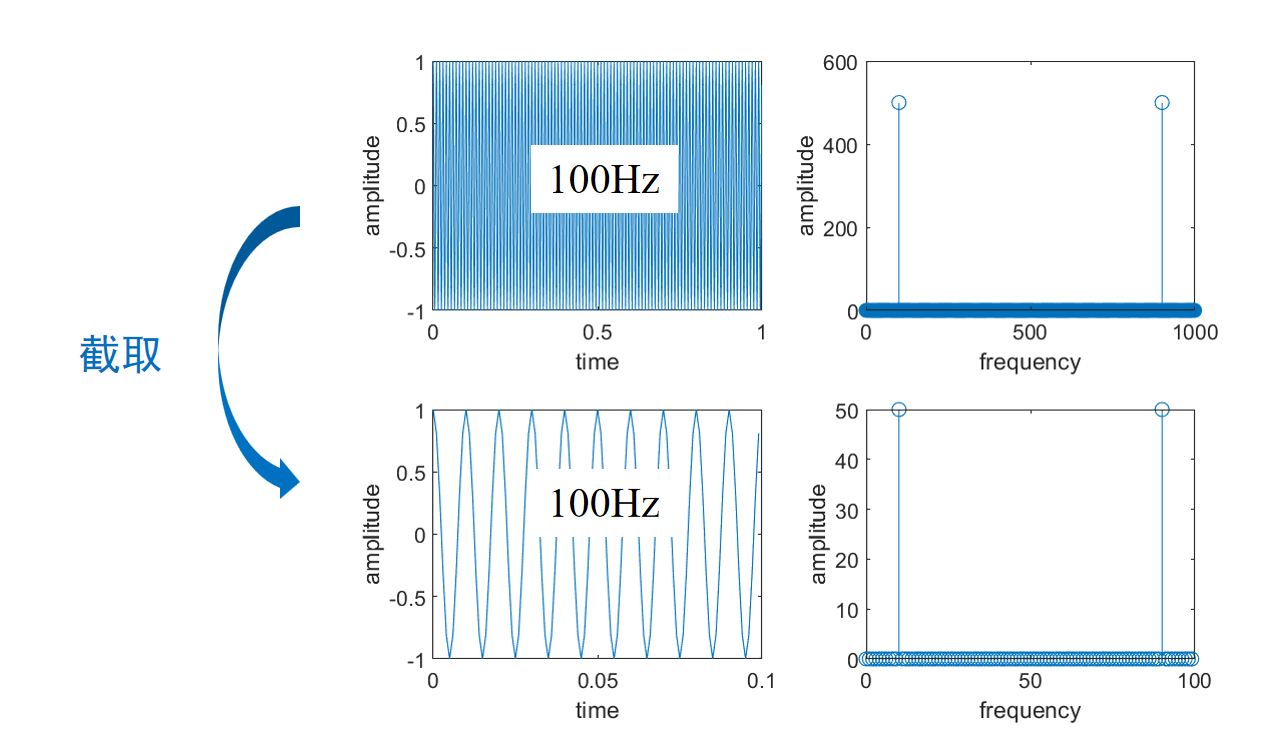
image

图1 未发生频谱泄露

为何强调恰好10个周期？把信号频率改成121Hz，这样100个点的采样结果就不能包含完整的周期了，如图2所示。
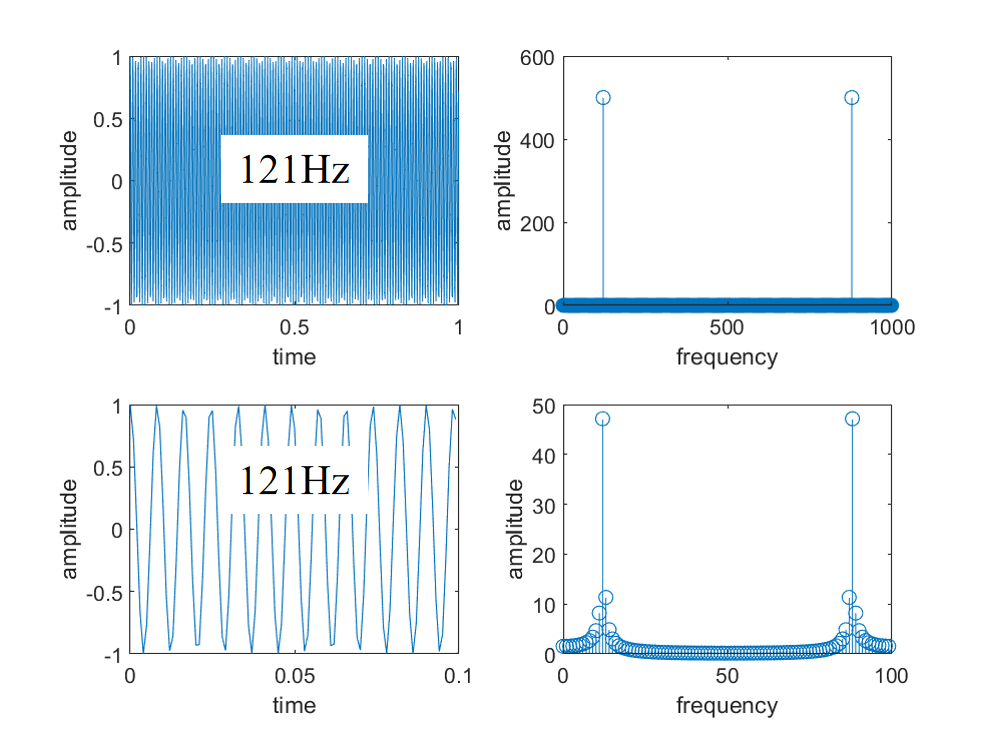
image

图2 发生频谱泄露

我们知道，DFT（Discrete Fourier Transform，离散傅里叶变换），为了得到离散的频谱，在频域相当于与周期冲激序列进行相乘，在时域对应的就是与周期冲激序列进行卷积，也就是周期延拓。它分析的其实是截取的这一段信号的周期延拓结果。如果不能恰好包含完整的周期，那周期延拓后就不能很好的对接上，从而引入了新的频率成分，如图3所示[2]，看起来就是原来的峰值会有所降低，同时在尾部产生了类似拖尾的效果。
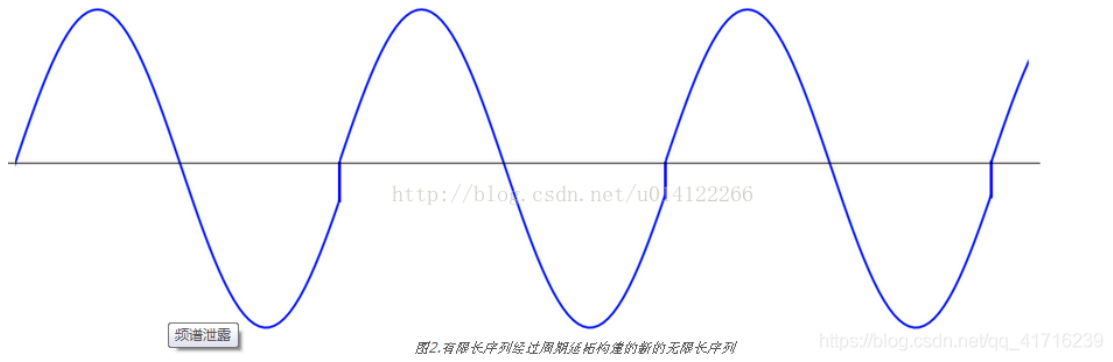
image

图3 周期延拓

这一现象产生的主要原因就是矩形窗的频谱特性，这篇文章中介绍的非常详细：知乎：频谱泄露

修改的周期图法

修改的周期图法在计算 DFT 之前对时域信号进行加窗，以平滑信号的边缘。 这具有降低旁瓣高度或频谱泄漏的效果。对于非矩形窗口，截断信号的端点平滑衰减，因此引入的杂散频率不那么严重。 另一方面，非矩形窗也加宽了主瓣，导致分辨率降低。

矩形窗和Hamming窗的频谱特性比较如图4所示。

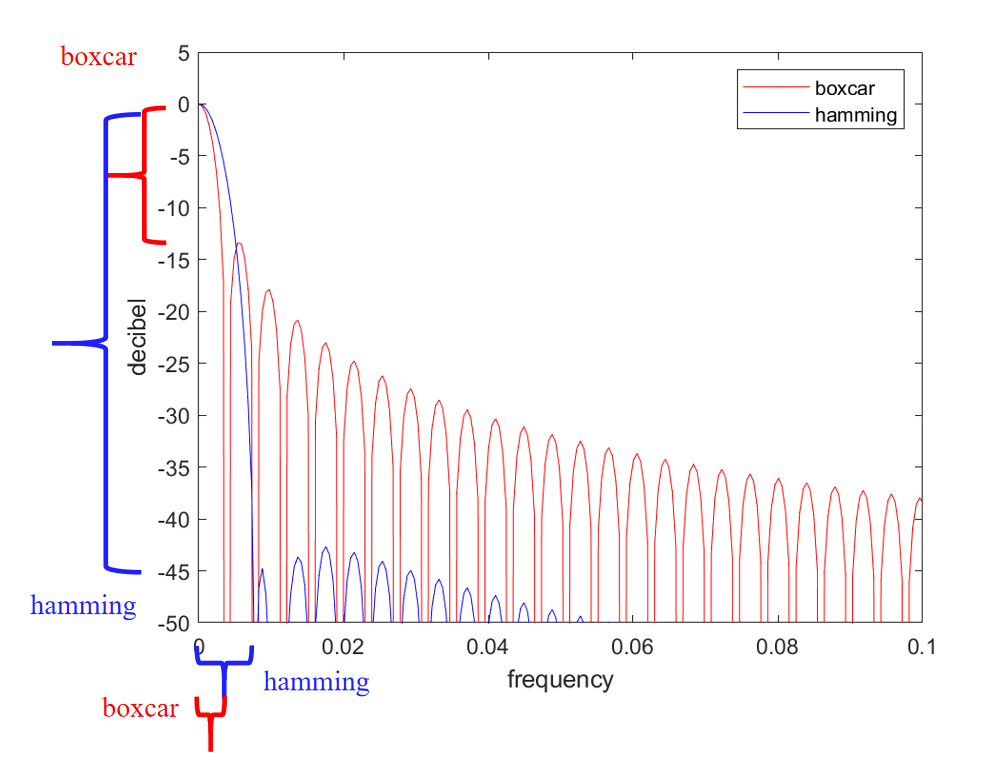
image

图4 矩形窗和汉明窗的频谱特性 

%% boxcar vs. hamming
clear,clc
close all;

N=256; % window length
x=boxcar(N);
z=hamming(N);

X2=fft(x,N*8);
X2_abs=abs(fftshift(X2));
X2_dB=20*log10(X2_abs/(max(X2_abs))+eps); % decibel

Z2=fft(z,N*8);
Z2_abs=abs(fftshift(Z2));
Z2_dB=20*log10(Z2_abs/(max(Z2_abs))+eps);
freq2=(-N*4:N*4-1)/(N*8); 
figure;
plot(freq2,X2_dB,'r');
hold on;
plot(freq2,Z2_dB,'b');
axis([0 0.1 -50 5]);
xlabel('frequency'); ylabel('decibel');
legend('boxcar','hamming');
set(gcf,'color','w');

Welch方法

Welch 提出了一种改进的 PSD 估计方法。该方法将时间序列数据划分为数段（可能重叠），计算每个段的修改的周期图，然后平均 PSD 估计值，如图5所示。Matlab工具箱函数 pwelch 实现了 Welch 的方法。
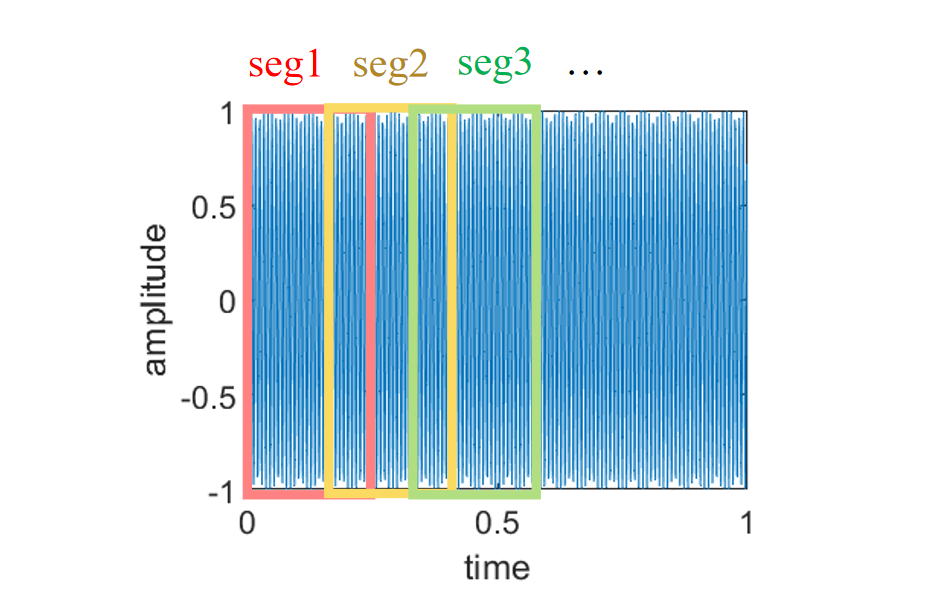
image

图5 Welch's method

相比于整个采样数据的单个周期图估计，修改后的周期图的平均倾向于减小估计的方差。尽管段之间的重叠引入了冗余信息，但这种影响通过使用非矩形窗口而减弱，这降低了每一段的末端样本（重叠的样本）的重要性或权重。

然而，如上所述，减短的数据记录和非矩形窗口的组合使用会导致估计的分辨率降低。总之，在方差减少和分辨率之间存在折衷。可以修改 Welch 方法中的参数以获得相对于周期图的改进估计，尤其是在 SNR 较低时可以获得更好的估计效果。

对于这种估计方法，MATLAB给出了pwelch函数：Matlab 帮助中心：Pwelch

这里给出我自己写的使用fft复现的welch方法，注意我代码中给出的估计结果是功率谱而非功率谱密度，如果要求功率谱密度，还需要除以采样率。pwelch函数在输入的最后一项指定'power'也可以计算功率谱。

% Welch's method for estimating power spectrum.
%   x       -- Input signal, must be vector.
%   window  -- Window sequence.
%   overlop -- Overlop size, must be less than the size of window.
%   nfft    -- FFT point.
%   fs      -- Sampling rate.

function varargout =dwelch(x,window,overlap,nfft,fs)

    nargoutchk(0,2);

    %calculating window sliding step for iteration
    winsize = length(window);
    step = winsize - overlap;
    iter = 1 + (length(x) - winsize)/step;

    %start and end index of first window/segment
    istart = 1;
    iend = istart + winsize - 1;

    % resize ....
    fft1 = zeros(nfft,iter);
    %start calculating fft for each window
    for i=1:iter
        %apply window
        x_win(istart:iend) = x(istart:iend).*window;

        %calculate fft
        fft1(:,i) = fft(x_win(istart:iend),nfft);

        %move to next window segment
        istart = istart + step;
        iend = iend + step;
    end

    %obtain scale to create modified periodogram
    scale = 1/sum(window)^2;

    %averaging window result and apply the scaling
    psd = zeros((nfft/2)+1,size(fft1,2));

    for i=1:iter
        psd = psd + fft1(1:(nfft/2)+1,i).*conj(fft1(1:(nfft/2)+1,i));
    end

    psd = psd.*scale./iter;

    %multiply by 2 except dc.
    psd(2:end) = psd(2:end).*2;

    pxx = psd;
    f = (fs/nfft)*(0:1:nfft/2);

    if nargout == 0
        plot(f,pxx);
        title('Welch PSD estimation');
        xlabel('Normalized frequency(\pi rad/sample)');
        ylabel('Power(W/(rad/sample))');
    elseif nargout == 1
        varargout = {pxx};
    elseif nargout == 2
        varargout = {pxx,f};
    end
end

纠正系数

在加窗时，做FFT分析的信号能量有所衰减，因此需要乘以一个相应的纠正系数（Correction Factor），这个纠正系数\(u\)的计算方式如下：

\[u = 1/(\sum win)^2 \]

比较

概览
周期图法 修改的周期图法 Welch方法
分辨率 最优 适中 最差
方差 最差 适中 最好
实现复杂度 简易 适中 复杂
定量比较

参考资料

  1. https://blog.csdn.net/qq_41639829/article/details/123756158 ↩︎

  2. https://blog.csdn.net/qq_41716239/article/details/105134887 ↩︎

posted @ 2022-10-14 22:30  devindd  阅读(717)  评论(0)  编辑  收藏  举报