5G-NR中的CFO估计技术

CFO的影响

在接收机接收信号的过程中，我们期望使用与发射机频率相同的本地振荡器，如果这二者的频谱不匹配，就会产生频率偏移。同时，基站和用户之间的相对运动会产生多普勒效应（Doppler Effect），从而造成接收机的频率偏移，关于多普勒效应的具体内容参见：Wikipedia-Doppler effect

定义归一化频偏为，频偏值与子载波间隔的比值，$\varepsilon = \frac{f_{offset}}{\Delta f}$，定义整数倍频偏（Integer Carrier Frequency Offset，IFO）和小数倍频偏（Fractional Carrier Frequency Offset，FFO）分别为 $\varepsilon_i$ 和 $\varepsilon_f$，满足 $\varepsilon_i+\varepsilon_f=\varepsilon$，其中 $\varepsilon_i=\lfloor \varepsilon \rfloor$。
由于OFDM使用频分复用，子载波间是正交的，这种频谱偏差会导致采样点的偏移，从而造成子载波间干扰（Inter Carrier Interface, ICI），如图1所示^[1]。但是整数倍的偏移值和小数倍的偏移值造成的影响有所差异，下面分为两节介绍。

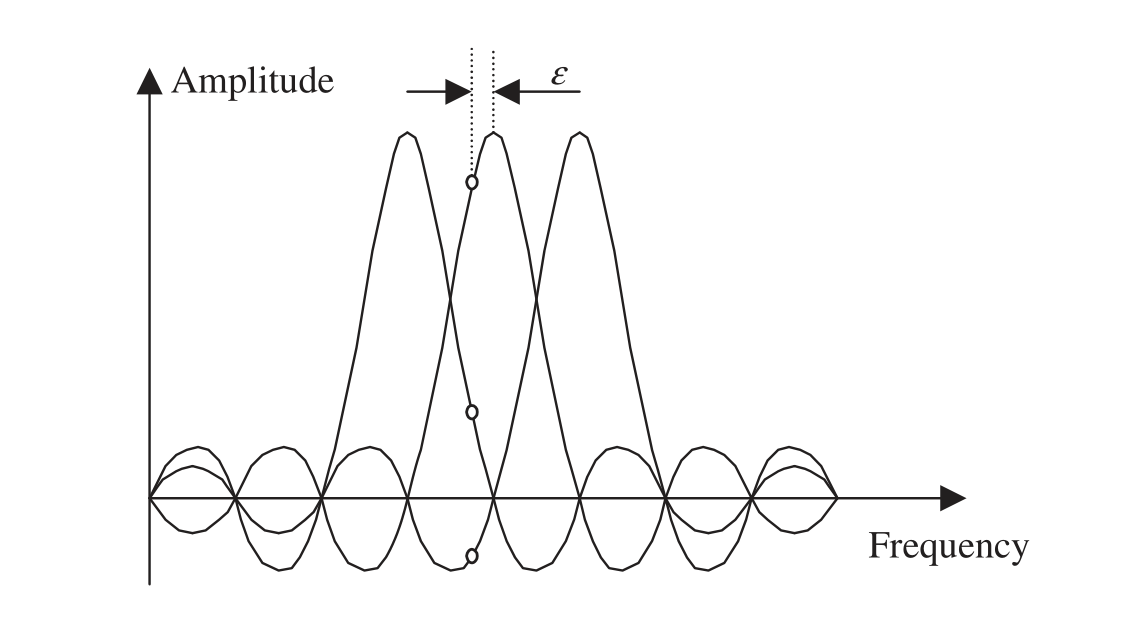
图1 CFO造成的子载波间干扰

参考资料^[1:1]中给出的CFO对接收机采样信号相位的影响的图也在这里贴一下，如图2所示，可以看到频偏越小，越接近原始信号，相位没有偏差，频偏越大，相位误差就积累越大。这个差值实际上需要在估计出频偏以后进行补偿来纠正，这部分内容在后面介绍。

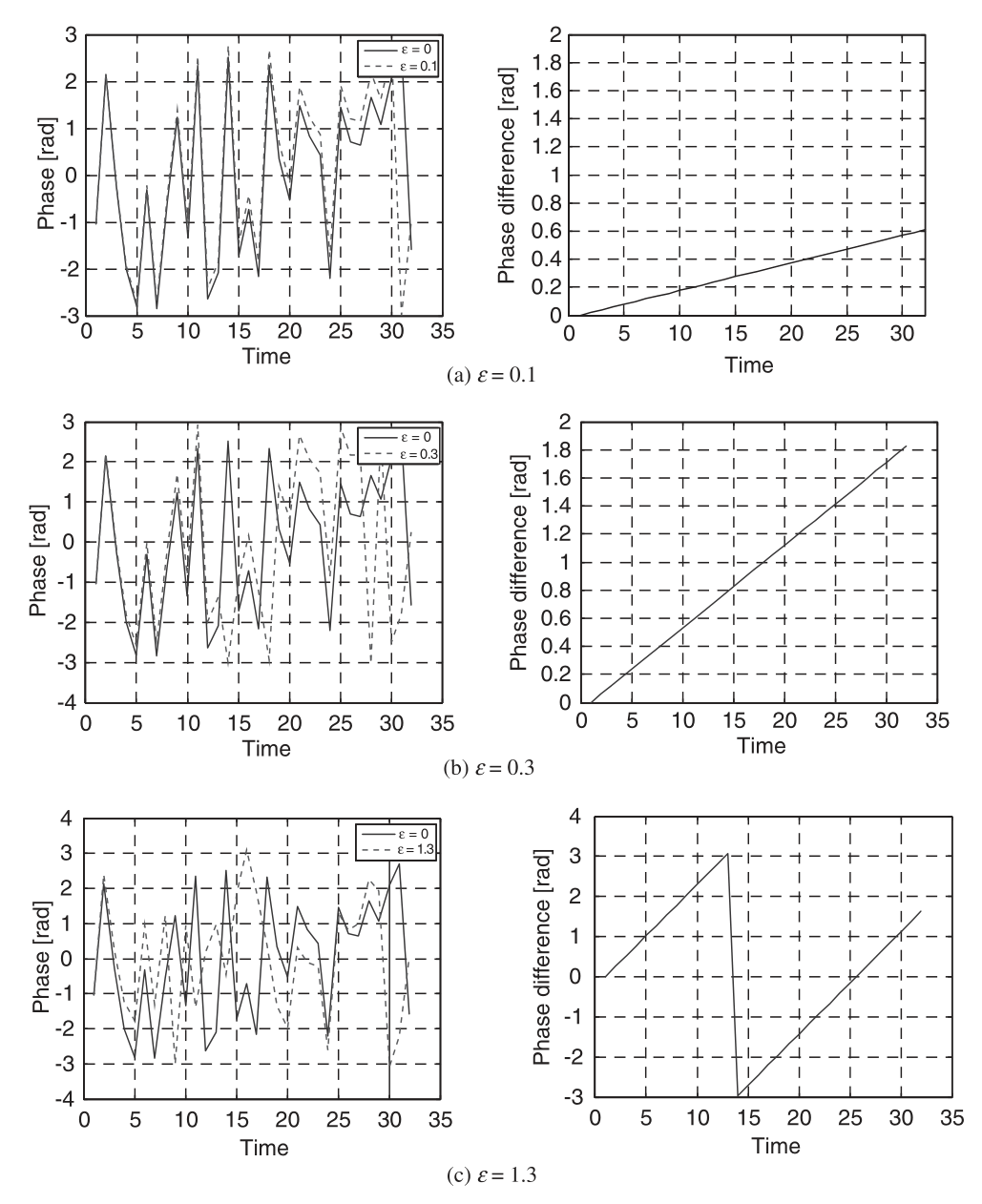
图2 CFO对相位的影响

整数倍频偏的影响

整数倍频偏 $\varepsilon_i$ 是一个整数值，收到整数倍频偏影响的信号可以写为 $x[n]e^{j2\pi\varepsilon_i n/N}$，由DFT的频移特性，对应到频域的信号为 $X[k-\varepsilon_i]$，也就是频域的循环移位。

为什么信号要乘以 $e^{j2\pi\varepsilon n/N}$?
考虑子载波间隔 $\Delta f$, 在时域上存在频偏的连续信号 $\hat{x}(t)=x(t)e^{j2\pi f_{offset} t}$, 对其进行采样, 则有
$\hat{x}[n]=x[n]e^{j2\pi (\varepsilon \cdot \Delta f)(n/Fs)}=x[n]e^{j2\pi (\varepsilon \cdot \Delta f)(n/(N\cdot \Delta f))}=x[n]e^{j2\pi \varepsilon n/N}$

小数倍频偏的影响

小数倍频偏不再是整数值，因此不再具有以上特性，小数倍频偏的推导公式太长，我这里也不再手敲了，直接放出参考资料^[1:2]中的截图，如图3所示。

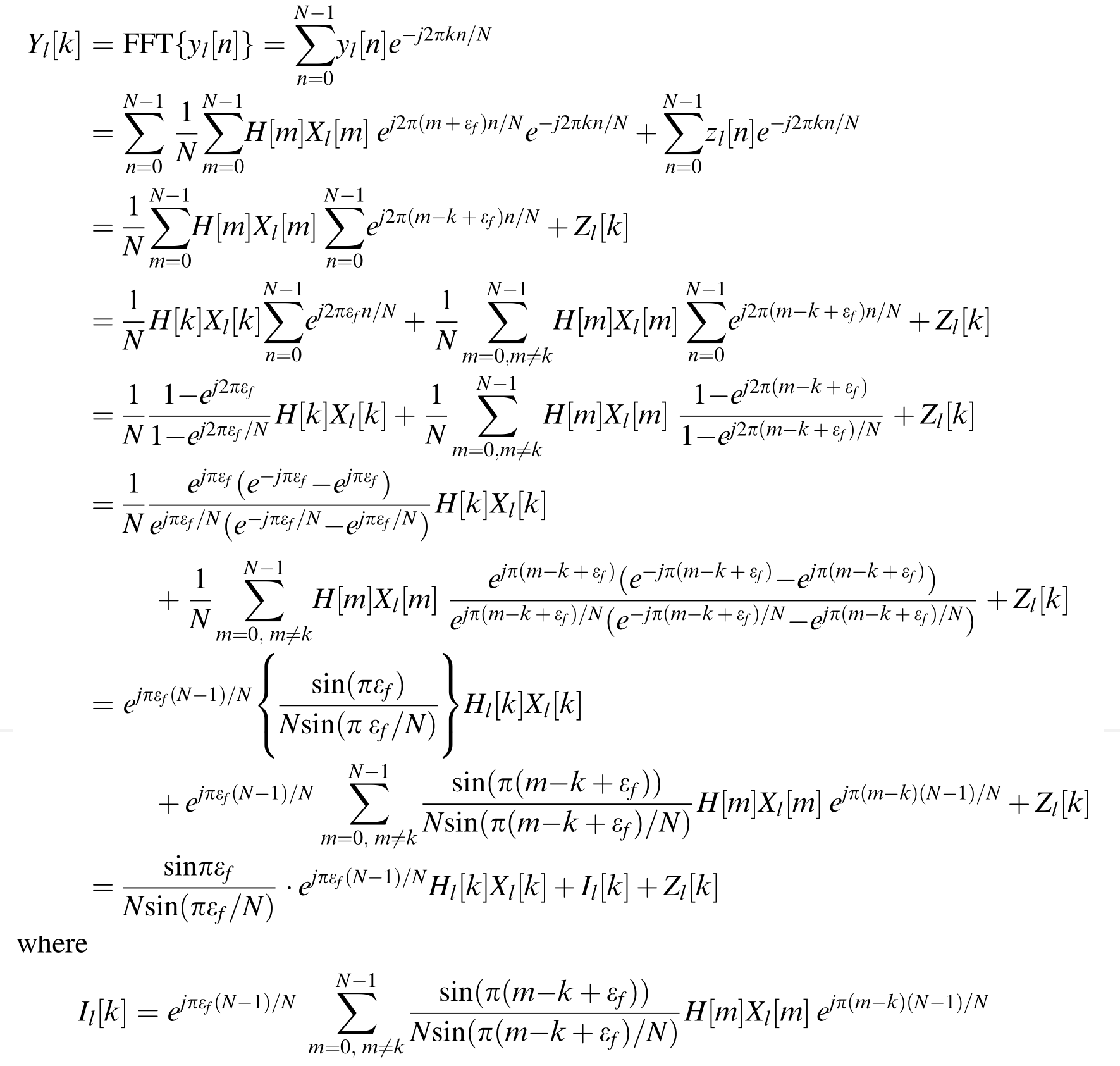
图3 小数倍频偏的影响

关于CFO对星座图的影响，我这里在STO那份代码的基础上简单修改了一下，

clear,clc
close all
rng(0);
Nfft = 4096; % FFT size
Ncp = 1024;  % extended CP
Nofdm = Nfft+Ncp;
RB = 64; % resource block num
Qm = 2; % modulation order
Ebn0 = 20;
cfo = 0.3; % normalized cfo
SNR = Ebn0+10*log10(Qm)+10*log10(RB*12/Nfft);
b = pskmod(randi([0,3],RB*12,1),4,0.25*pi); % QPSK
Ng = Nfft-RB*12; % Guard
x = [zeros(Ng/2,1);b;zeros(Ng/2,1)];
x_tx = ifft(fftshift(x));
x_tx = [x_tx(Nfft-Ncp+1:Nfft);x_tx]; % add CP
nn=0:length(x_tx)-1; 
x_tx1 = x_tx.*(exp(1i*2*pi*cfo*nn/Nfft).'); % Nfft as sampling rate

x_ch = awgn(x_tx,SNR,'measured');
x_ch1 = awgn(x_tx1,SNR,'measured');
y_rx = x_ch(Ncp+1:Nofdm);
y_rx1 = x_ch1(Ncp+1:Nofdm);

y = fftshift(fft(y_rx));
y1 = fftshift(fft(y_rx1));
yb = y(Ng/2+1:Ng/2+RB*12);
yb1 = y1(Ng/2+1:Ng/2+RB*12);

figure;
% set(0,'defaultfigurecolor','w');
subplot(121);
plot(yb,'.'); axis equal; axis([-1.2,1.2,-1.2,1.2]); hold on;
title('scatter without cfo');
subplot(122);
plot(yb1,'.'); axis equal;axis([-1.2,1.2,-1.2,1.2]); 
title('scatter with cfo');

简单观察一下，它其实是对接收信号的幅度和相位都有所影响，而不仅仅是移动了几个频域标号。具体这部分的影响将在CFO补偿部分讲。

CFO估计技术

时域CFO估计技术

基于CP的时域CFO估计

时域上用来估计的已知条件无非就是CP和训练序列。下面介绍一下基于CP的CFO估计方法。

首先，受CFO影响的信号可以写为， $x[n]e^{j2\pi\varepsilon n/N}$，这里的 $\varepsilon$ 是个定值，由于循环前缀的特性，CP和尾部对应的部分，这里的n正好差了N个长度，那么我们用CP部分的共轭与尾部的部分相乘，就可以得到一个定值 $e^{j2\pi\varepsilon}$ ，这就是时域估计CFO的基础，对这个定值求角，然后除以 $2\pi$ 就可以得到估计值。写成公式的形式如下：

\[\hat{\varepsilon}=\frac{1}{2\pi}arg \{\sum_{n=-N_G}^{-1}y_l^*[n]y_l[n+N]\} \]

由于arg{}其实就是 $tan^{-1}()$，所以这样得到的值是 $[-\pi,\pi)/2\pi=[-0.5,0.5)$，也就是说，$|\hat{\varepsilon}|<0.5$ ，只能用来估计小数频偏。

基于训练序列的CFO估计

基于训练序列的估计方法与基于CP的方法类似。CP是利用时域上循环前缀和尾部重复的特性来进行估计，基于训练序列的方法在频域上插0，在时域上就会产生两段重复的序列，利用这个重复的信息就可以完成估计。

训练序列的频域结构如下：

\[X_l[k]=\left \{ \begin{array}{lc} A_m, & k=D\cdot i,i=0,1,\cdots , (N/D-1) \\ 0, & otherwise \end{array} \right. \]

关于为什么插0，时域上就会重复可以看我的这篇文章，博客园-STO估计。

频偏估计结果为：

\[\hat{\varepsilon}=\frac{D}{2\pi}arg\left \{ \sum_{n=0}^{N/D-1} y_l^*[n]y_l[n+N/D] \right \} \]

它使用时域上，单个符号内重复的两端进行估计，这两段的距离与CP方法估计不同，不再是N，而是 $N/D$ ，因此差的相位是 $2\pi\varepsilon(N/D)/N=2\pi\varepsilon/D$。

同时，可以注意到，这种方法估计出来的频偏，不再是介于-0.5到0.5之间，而是 $|\varepsilon|<D/2$，所以它具有更好的估计范围。

频域CFO估计技术

Moose方法

Moose估计方法，在参考资料^[1:3]中是这样描述的。

如果传输两个相同的训练符号，那他们对应的信号与频偏 $\varepsilon$ 的关系如下所示：

\[y_2[n]=y_1[n]e^{j2\pi N\varepsilon/N}\leftrightarrow Y_2[k]=Y_1[k]e^{j2\pi \varepsilon} \]
根据频域上的对应关系，则CFO可以由下式进行估计：

\[\hat{\varepsilon}=\frac{1}{2\pi}arg\left \{\sum_{k=0}^{N-1}Y_1^*[k]Y_2[k] \right \} \]

是不是跟基于训练序列的时域估计类似？说实话我也没太搞明白，既然时域上和频域上差的相位差一样，那在时域上应该也是一样的。

这种方法估计的范围也是 $[-0.5,0.5)$ 。但是，如果每个OFDM符号都有CP的存在，两个符号的间隔就不再是N，相应的估计值就要乘以一个 $N_{fft}/(N_{fft}+N_{cp})$，也就是估计的精度会有所下降。

Classen方法

Classen方法是使用信道特性来进行估计的方法。假设我们有发射端导频信号 $x_p[n]$ ，信道冲激响应（离散）为 $h[n]$ ，归一化频偏为 $\varepsilon$ ，先不考虑噪声的影响，接收端导频信号为 $y_p[n]=x_p[n]*h[n]\cdot e^{j2\pi\varepsilon n/N}$ ，我们在频域上对发射端导频共轭相乘接收端导频（由于小数倍频偏在频域的情况过于复杂，这里就不再公式给出了，参考“CFO的影响“一节中的图3），那么在时域上，由于导频信号功率为1，就可以得到 $h[n]e^{j2\pi \varepsilon n/N}$ 。到了这里，就可以看出它与Moose方法的联系了。

\[\hat{\varepsilon}=\frac{1}{2\pi\cdot T\cdot D}arg\left \{\sum_{j=1}^{L-1} Y_{l+D}[j]X_{l+D}^*[j]\cdot(Y_l[j]X_l^*[j])^* \right \} \]

首先介绍一下，使用块状导频进行估计时的情况，两个导频信号的相位差值是一个定值，如果是连续的两个，那这个定值就是 $e^{j2\pi \varepsilon(N_{fft}+N_{cp})/N_{fft}}$，如果是非连续的，而是差了D个符号位置，那这个相位差就是 $e^{j2\pi\varepsilon D(N_{fft}+N_{cp})/N_{fft}}$ ，剩下的过程同Moose方法，求 $tan^{-1}()$ ，然后乘以相应的系数就可以得到 $\varepsilon $ 。值得注意的是，由于我们求角的范围是 $[-\pi,pi)$ ，那得到的归一化频偏值的范围为 $|\varepsilon|\leq\frac{1}{2}\cdot\frac{N_{fft}}{N_{fft}+N_{cp}}\cdot \frac{1}{D}$，其中D是两个相邻导频符号的符号索引的差值。可见，Classen方法估计出来的频偏范围要比前面几种方法都小。

几种CFO估计技术的Matlab代码

首先是主文件，这个文件仿真了一种很简单的情况，用到的子函数有 add_pilot，cfo_est，cfo_mtx，也分别在这里给出。

仿真中做了4096点FFT，CP长度1024，发送块状导频，分别在符号1，2，6，9的位置发送。两个符号索引的最大差值是4，因此Classen方法估计的频谱范围是（归一化的） $0.5\cdot\frac{4096}{4096+1024}\cdot\frac{1}{4}=0.1$。其中，导频在频域上隔1插0，可以用于时域上估计。

% test_sto_est.m
% Author: Devin - balddonkey@outlook.com
% 10/18/2022
clear,clc
close all
global ShowFigure;
ShowFigure=1;
rng(0);
Nfft = 4096; % FFT size
Ncp = 1024;  % extended CP
Nofdm = Nfft+Ncp;
RB = 64; % resource block num
Qm = 2; % modulation order
Ebn0 = 20;
cfo = 0.1; % Normalized cfo by subcarrier spacing
% scs = 2e3; % subcarrier spacing
Nsymb = 12;
Nps = 2; % Pilot spacing.
dmrs_pos = [1,2,6,9]; % Two consecutive identical pilot for Moose method.
Ng = Nfft-RB*12; % Guard
SNR = Ebn0+10*log10(Qm)+10*log10(RB*12/Nfft);
%% transmitter
b = pskmod(randi([0,3],RB*12,Nsymb-numel(dmrs_pos)),4,0.25*pi); % QPSK
tx_dmrs = add_pilot(zeros(RB*12,numel(dmrs_pos)),RB*12,Nps); % identical tranined symbol

% resource mapping
dmrs_idx = 1;
data_idx = 1;
x = zeros(RB*12,Nsymb);
for l = 1:Nsymb
    if ismember(l,dmrs_pos)
        x(:,l) = tx_dmrs(:,dmrs_idx); % configuration type 1 for pusch
        dmrs_idx = dmrs_idx+1;
    else
        x(:,l) = b(:,data_idx);
        data_idx = data_idx+1;
    end
end

x1 = [zeros(Ng/2,Nsymb);x;zeros(Ng/2,Nsymb)];
x_tx = ifft(fftshift(x1,1)).*sqrt(Nfft);
x_tx = [x_tx(Nfft-Ncp+1:Nfft,:);x_tx]; % add CP

%% channel
% x_ch = x_tx;
x_tx = x_tx(:);

nn=0:length(x_tx)-1; 
x_tx1 = x_tx.*(exp(1i*2*pi*cfo*nn/Nfft).'); % Add cfo, Nfft as sampling rate
% x_tx1 = x_tx.*(exp(1i*2*pi*cfo*nn/(Nfft*scs)).');

% x_ch = awgn(x_tx1,SNR,'measured');
x_ch = x_tx1;
% x_ch = [zeros(sto,1);x_ch]; % add sto

y_rx = zeros(Nofdm,Nsymb);
for l = 1:Nsymb
    y_rx(:,l) = x_ch(Nofdm*(l-1)+1:Nofdm*l);
end
y_rx_1 = y_rx(Ncp+1:Nofdm,:);

%% receiver
y = fftshift(fft(y_rx_1)./sqrt(Nfft),1);
yb = y(Ng/2+1:Ng/2+RB*12,:);
dmrs_idx = 1;
data_idx = 1;
rx_dmrs = zeros(RB*12,numel(dmrs_pos));
rx_data = zeros(RB*12,Nsymb-numel(dmrs_pos));
for l = 1:Nsymb
    if ismember(l,dmrs_pos)
        rx_dmrs(:,dmrs_idx) = yb(:,l);
        dmrs_idx = dmrs_idx+1;
    else
        rx_data(:,data_idx) = yb(:,l);
        data_idx = data_idx+1;
    end
end

cfo_cp = cfo_est(y_rx,Nfft,Ncp,'cp')
cfo_pilot = cfo_est(y_rx_1(:,dmrs_pos),Nfft,Nps,'pilot')
cfo_moose = cfo_est(y(:,dmrs_pos(1:2)),Nfft,Ncp,'moose')
cfo_classen = cfo_est(rx_dmrs,tx_dmrs,Nfft,Ncp,dmrs_pos,'classen')

% compensation for cfo in frequency domain
mtx = cfo_mtx(cfo_cp,Nfft);
yc = mtx*y.*exp(-1i*2*pi*cfo_cp*(Ncp+Nofdm*(0:Nsymb-1))/Nfft);
yc1 = yc(Ng/2+1:Ng/2+RB*12,:);
data_idx = 1;
rx_data1 = zeros(RB*12,Nsymb-numel(dmrs_pos));
for l = 1:Nsymb
    if ismember(l,dmrs_pos)
    else
        rx_data1(:,data_idx) = yc1(:,l);
        data_idx = data_idx+1;
    end
end

if ShowFigure == 1
    figure;
    % set(0,'defaultfigurecolor','w');
    subplot(121);
    plot(rx_data1,'.'); axis equal;axis([-1.2,1.2,-1.2,1.2]); 
    title('scatter with cfo compensated');
    subplot(122);
    plot(rx_data,'.'); axis equal;axis([-1.2,1.2,-1.2,1.2]); 
    title('scatter with cfo not compensated');
end

其中用到的函数如下：
加导频，使用恒幅0自相关序列。
add_pilot.m

function xp=add_pilot(x,Nfft,Nps)
% CAZAC (Constant Amplitude Zero AutoCorrelation) sequence –> pilot
% Nps : Pilot spacing
% MIMO-OFDM Wireless Communications with MATLAB

if nargin <3, Nps=4; end
Np=Nfft/Nps; % Number of pilots
xp=x; % Prepare an OFDM signal including pilot signal for initialization
for k=1:Np
    xp((k-1)*Nps+1,:)=exp(1i*pi*(k-1)^2/Np); % Eq.(7.17) for Pilot boosting
end

使用四种估计算法，分别是时域CP，时域训练序列，频域Moose，频域Classen方法。
cfo_est.m

function varargout = cfo_est(varargin)
% Author: Devin - balddonkey@outlook.com
% 10/17/2022
% Carrier Frequency Offset Estimation.
% cfo = cfo_est(y,Nfft,Ng,'cp');
% cfo = cfo_est(y,Nfft,Nps,'pilot');
% cfo = cfo_est(y,Nfft,Ng,'moose'); where, y has the size of N*2.
% cfo = cfo_est(y,xp,Nfft,Ng,idx,'classen');
% Inputs:
%   y      : received symbols in time domain or frequency domain.
%   xp     : transmitter pilot symbol in frequency domain.
%   Nfft   : FFT points.
%   Ncp    : CP length.
%   Nps    : pilot spacing, must be larger than 1.
%   idx    : index of pilot location in slots, must be a vector.
%   method : 'cp','pilot', based on time domain;
%            'moose','classen', based on frequency domain.
% Outputs:
%   cfo_est  : CFO estimation result.

global ShowFigure;

narginchk(1,6);
nargoutchk(0,2);

% parse input arguments.
lenargin = length(varargin);
if lenargin>=1
    y = varargin{1};
    method = 'cp';
    if lenargin >= 2
        method = varargin{lenargin};
    end
end

% estimate cfo.
if strcmpi(method,'cp')
    Nfft = varargin{2};
    Ncp = varargin{3};
    cfo_est = angle(y(1:Ncp,1)'*y(Nfft+1:Nfft+Ncp,1))/(2*pi);
    cfo_est = mean(cfo_est);
elseif strcmpi(method,'pilot')
    Nfft = varargin{2};
    Nps = varargin{3};
    cfo_est = angle(y(1:Nfft/Nps,1)'*y(Nfft/Nps+1:2*Nfft/Nps,1)).*Nps/(2*pi); 
    cfo_est = mean(cfo_est);
elseif strcmpi(method,'moose')
    Nfft = varargin{2};
    Ncp = varargin{3};
    cfo_est = angle(y(:,1)'*y(:,2))./(2*pi);
    cfo_est = cfo_est*Nfft/(Nfft+Ncp);
elseif strcmpi(method,'classen')
    xp = varargin{2};
    Nfft = varargin{3};
    Ncp = varargin{4};
    idx = varargin{5};

    arg = angle((y(:,2:end).*conj(y(:,1:end-1))).'*...
        (conj(xp(:,2:end)).*xp(:,1:end-1)));
    arg = diag(arg).';
    cfo_est = arg./(2*pi*(idx(2:end)-idx(1:end-1)));
    cfo_est = mean(cfo_est).*Nfft./(Nfft+Ncp);
else
    error('unsupported estimation algorithm');
end

% arguments out.
if nargout == 0 || 1
    varargout = {cfo_est};
elseif nargout == 2
    varargout = {cfo_est,0};
end

小数倍CFO补偿矩阵。
cfo_mtx.m^[2]

function varargout = cfo_mtx(varargin)
% Author: Devin - balddonkey@outlook.com
% 10/18/2022
% equalization banded matrix for cfo.
% Inputs:
%   cfo      : normalized cfo by subcarrier frequency.
%   N        : FFT point.
%   tau      : bandwidth of banded matrix.
% Outputs:
%   mtx      : banded matrix for qualization.
%   mtx_full : full bandwidth banded matrix.

global ShowFigure;

narginchk(2,3);
nargoutchk(0,2);

% parse input arguments.
cfo = varargin{1};
N = varargin{2};
if nargin == 3
    tau = varargin{3};
else
    tau = -1; % full bandwidth
end

m = 0:N-1;
mtx = zeros(N);
mtx_full = zeros(N);
for k = 0:N-1
    mtx(k+1,:) = sin(pi*(m-k+cfo))./(N*sin(pi*((m-k+cfo)/N)))...
        .*exp(1i*pi*(m-k+cfo)*(N-1)/N);
end

if tau ~= -1
    mtx_full = mtx';
    mtx_banded = tril(ones(N),tau).*triu(ones(N),-tau);
    mtx = mtx.*mtx_banded;
end
mtx = mtx';

if nargout == 0 || 1
    varargout = {mtx};
elseif nargout == 2
    varargout = {mtx,mtx_full};
end

CFO补偿

CFO补偿原理

我们拿出“CFO的影响”一节中推导过程的最终结果来看，如图所示。

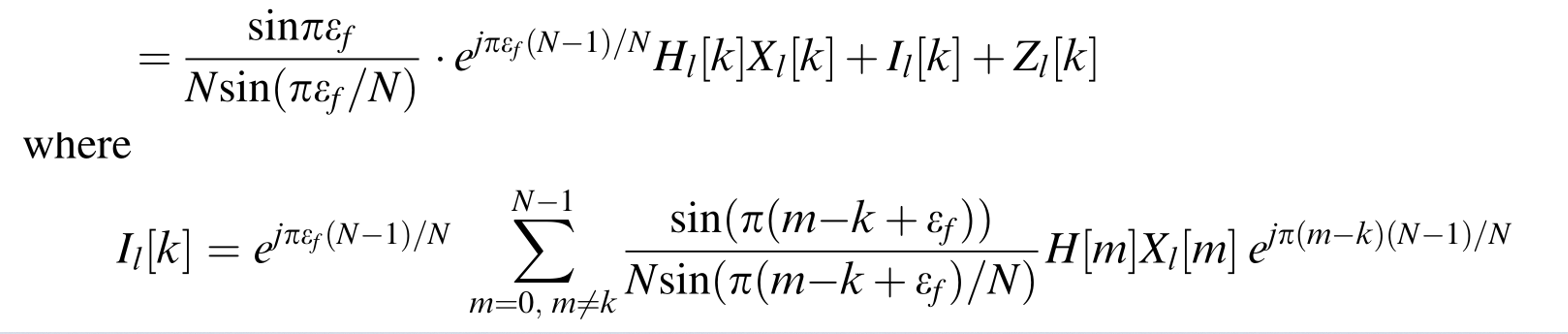
图X CFO的影响

虽然第一眼看上去很复杂，其实除去 $Z_l[k]$，别的项是可以进行合并的，合并后如下式所示：

\[Y_l[k]=\sum_{m=0}^{N-1}\frac{sin(\pi(m-k+\varepsilon_f))}{Nsin(\pi(m-k+\varepsilon_f)/N)}H[m]X_l[m]e^{j\pi(m-k+\varepsilon_f)(N-1)/N} \]

单拿出以下这部分：

\[\frac{sin(\pi(m-k+\varepsilon_f))}{Nsin(\pi(m-k+\varepsilon_f)/N)}e^{j\pi(m-k+\varepsilon_f)(N-1)/N} \]

这个就是CFO补偿矩阵。它的横纵索引分别是m和k，在m=k，也就是对角线的地方，取到 $\frac{sin(\pi\varepsilon_f)}{Nsin(\pi\varepsilon_f/N)}e^{j\pi\varepsilon_f(N-1)/N}$。第二行是第一行的循环右移，第三行是第二行的循环右移，依次类推。

在这种补偿方式下，每个频域采样值，需要进行N次乘法运算，一个OFDM符号需要 $N^2$ 次乘法运算。

注意：在频域进行CFO补偿时，需要对每个块进行初始相位补偿。

低复杂度CFO补偿

通过Maltab绘图，观察CFO影响系数的幅度值和相位值，自变量为 $m-k+\varepsilon_f$，其中 $m-k$ 的取值范围是 $[-(N-1):(N-1)]$，为了方便起见，观察 $[-10,10]$ 的图像如图X所示。对应的Matlab代码也在这里给出，修改cfo的范围即可。

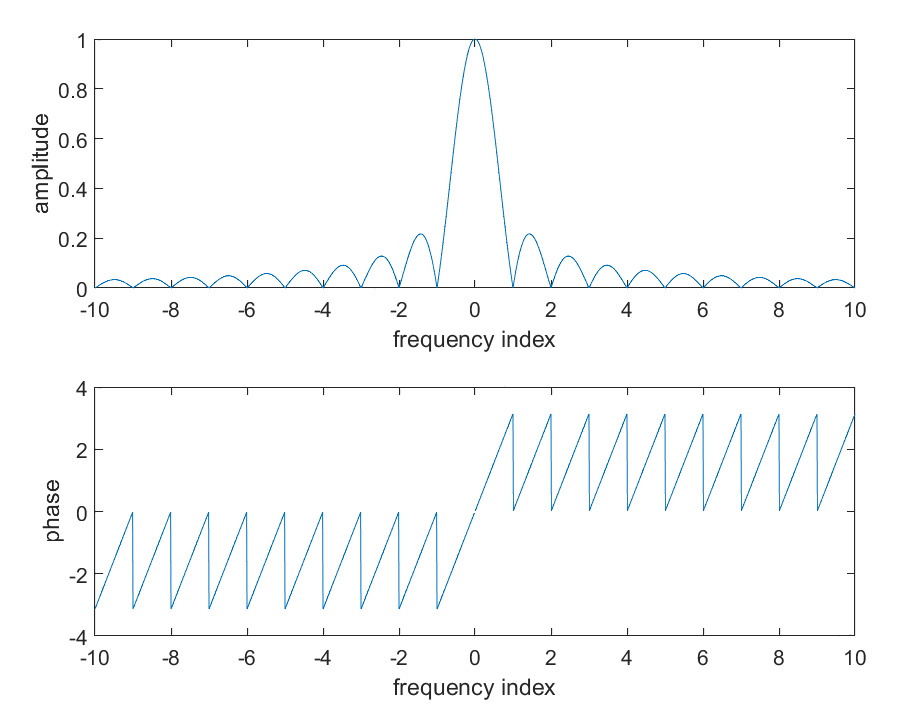
图X CFO对幅度和相位的影响

% test for cfo compensation factor.
% Author: Devin - balddonkey@outlook.com
% 10/18/2022
close all;

N = 4096;
cfo = -10:0.01:10;
y = sin(pi*(cfo)) ./ (N*sin(pi*((cfo)/N))) .* exp(1i*pi*(cfo)*(1-1/N));

figure;
subplot(211);
plot(cfo,abs(y));
xlabel('frequency index');
ylabel('amplitude');
subplot(212);
plot(cfo,phase(y));
xlabel('frequency index');
ylabel('phase');

通过观察可以发现，仅在自变量为0的地方幅值较高（也就是对角线部分），然后逐渐递减，在更远处，幅值约等于0。结合这个概念，论文^[2:1]中提出了一种低复杂度的CFO补偿方法，就是将原来的补偿矩阵简化为带限矩阵（banded matrix），只取对角线及其左右的 $\tau$ 个值用作CFO补偿，其余值全部设为0，这样大大简化了运算量。具体 $\tau$ 的取值对性能的影响，论文当中也给出了详细说明，这里不再展开。

这种低复杂度CFO补偿的MATLAB代码也整合进了前面给出的函数当中。

这里推荐一篇介绍CFO非常全面的文章，Wiley Online Library-CFO^[3]

参考资料

Cho, Yong Soo, et al. MIMO-OFDM wireless communications with MATLAB. John Wiley & Sons, 2010. ↩︎ ↩︎ ↩︎ ↩︎
Cao Z, Tureli U, Yao Y. Low-complexity orthogonal spectral signal construction for generalized OFDMA uplink with frequency synchronization errors. IEEE Trans Vehic Tech. 2007;56(3):1143-1154. ↩︎ ↩︎
Ramadan, Khaled, et al. "Joint low‐complexity equalization and CFO estimation and compensation for UWA‐OFDM communication systems." International Journal of Communication Systems 33.3 (2020): e3972. ↩︎

posted @ 2022-10-13 23:20 devindd 阅读(1800) 评论(0) 编辑收藏举报

刷新页面返回顶部