5G-NR中STO估计技术
STO的影响
STO(Symbol Time Offset)是指符号定时偏差。OFDM系统中,在发射端,我们会做IFFT进行OFDM调制,同时添加CP(Cyclic Prefix,循环前缀)。接收端则是该过程的逆过程,即去除CP,而后进行FFT。由于接收端不知道每个符号精确的起始位置,在进行符号同步时可能或提前或滞后给出一个起始信号,从而会对FFT的结果产生影响。
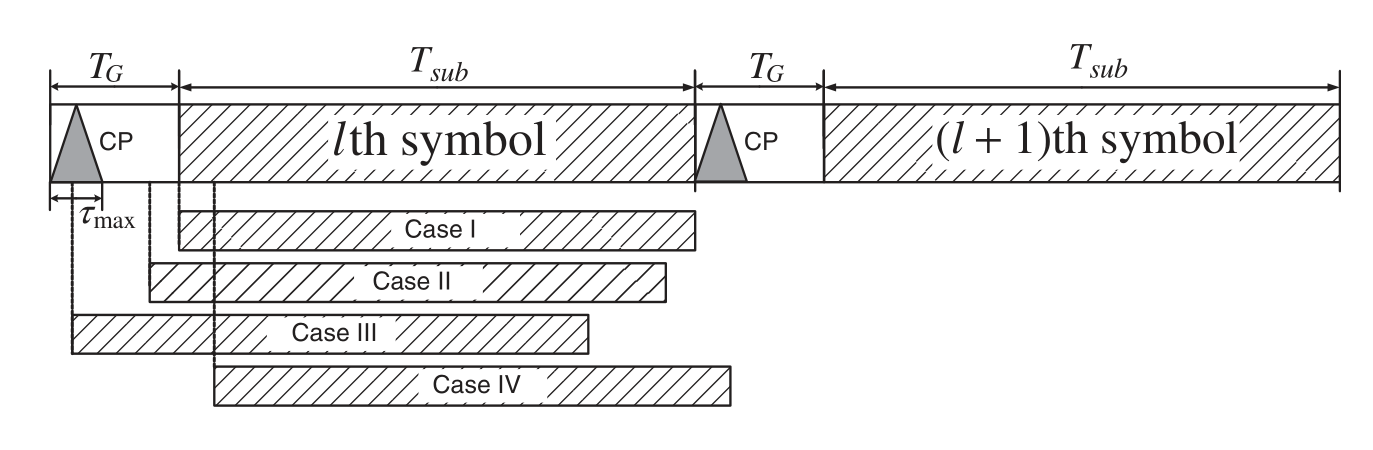
图1 4种OFDM符号起始点的情况
图1是《MIMO-OFDM Wireless Communications with MATLAB》一书中第5.1节给出的示意图[1],四种情况分别对应:
- 定时准确,FFT窗的起始点与OFDM符号去除CP后的起始点一致,这种情况下可以保持子载波频率成分的正交性,OFDM符号可以完美恢复;
- 定时提前,落在CP内,这种情况下FFT的输入信号是原信号的循环移位,假设偏移了\(\delta\)个值,那进行FFT的时域信号为 \(\{x_l[n+\delta]\}_{n=0}^{N-1}\) ,FFT后的频域结果为\[\begin{aligned} Y_l[k]&=\sum_{n=0}^{N-1}x_l[n-\delta]e^{-j2\pi nk/N}\\ &=\sum_{m=-\delta}^{N-1-\delta} x_l[m]e^{-j2\pi(m+\delta)/N}\\ &=\sum_{m=-\delta}^{1} x_l[m]e^{-j2\pi(m+\delta)/N}+\sum_{m=0}^{N-1} x_l[m]e^{-j2\pi(m+\delta)/N}-\sum_{m=N-\delta}^{N-1} x_l[m]e^{-j2\pi(m+\delta)/N}\\ \end{aligned}\]由于循环前缀的特性(将后半段放到前面),上面式子第一项与第三项相同,于是\[Y_l[k]=\left\{\sum_{n=0}^{N-1}x_l[n]e^{-j2\pi nk/N}\right\}\cdot e^{-j2\pi \delta k/N} \]对应频域点发生旋转,如图2所示
![image]()
图2 STO的影响
简单的matlab仿真代码如下:
clear,clc
close all
Nfft = 4096; % FFT size
Ncp = 1024; % extended CP
Nofdm = Nfft+Ncp;
RB = 64; % resource block num
Qm = 2; % modulation order
Ebn0 = 20;
sto = 64;
SNR = Ebn0+10*log10(Qm)+10*log10(RB*12/Nfft);
b = pskmod(randi([0,3],RB*12,1),4,0.25*pi); % QPSK
Ng = Nfft-RB*12; % Guard
x = [zeros(Ng/2,1);b;zeros(Ng/2,1)];
x_tx = ifft(fftshift(x));
x_tx = [x_tx(Nfft-Ncp+1:Nfft);x_tx]; % add CP
x_ch = awgn(x_tx,SNR,'measured');
y_rx = x_ch(Ncp+1:Nofdm); % remove cp without sto
y_rx1 = x_ch(Ncp+1-sto:Nofdm-sto); % with sto
y = fftshift(fft(y_rx));
y1 = fftshift(fft(y_rx1));
yb = y(Ng/2+1:Ng/2+RB*12);
yb1 = y1(Ng/2+1:Ng/2+RB*12);
figure;
% set(0,'defaultfigurecolor','w');
subplot(121);
plot(yb,'.'); axis equal; axis([-1.2,1.2,-1.2,1.2]); hold on;
title('scatter without sto');
subplot(122);
plot(yb1,'.'); axis equal;axis([-1.2,1.2,-1.2,1.2]);
title('scatter with sto');
- OFDM符号的定时起点在前一个OFDM符号的信道响应结束之前,因此,符号时序为时过早,无法避免ISI(Inter Symbol Interference,符号间干扰)。在这种情况下,子载波之间的正交性被ISI破坏,此外,还会有ICI(Inte Channel Interference,信道间干扰)发生。
- FFT窗包含下一个OFDM符号的循环前缀,此时也会发生符号间干扰。
STO估计技术
STO的估计主要分为时域估计技术和频域估计技术。
频域STO估计
基于导频的频域STO估计
频域STO估计主要借助于导频信息,也就是DMRS(De-Modulation Reference Symbol)符号。DMRS符号有一个重要的特性就是,每个子载波上的功率为1。
我们知道,在时域上的同步偏差,反映到频域上就是相位旋转,假设发射的导频信号为\(X_l(k)\),接收到的导频信号则为\(Y_l(k)e^{j2\pi\delta k/N}\),其中\(Y_l(k)=H_l(k)X_l(k)\)(理想情况下)。我们把接收到的信号与发射端的导频信号作相关(共轭相乘),再作IFFT转换到时域上,则有
其中,第三行到第四行是因为\(X_l(k)X_l^*(k)=1\),也是DMRS符号的一个特性。这样,反映到时域就是信道脉冲响应的移位。根据估计出的STO值可以对接收信号进行补偿,从而获得正确的星座图。
如图3和图4分别是DMRS信号相关峰值,和星座图。
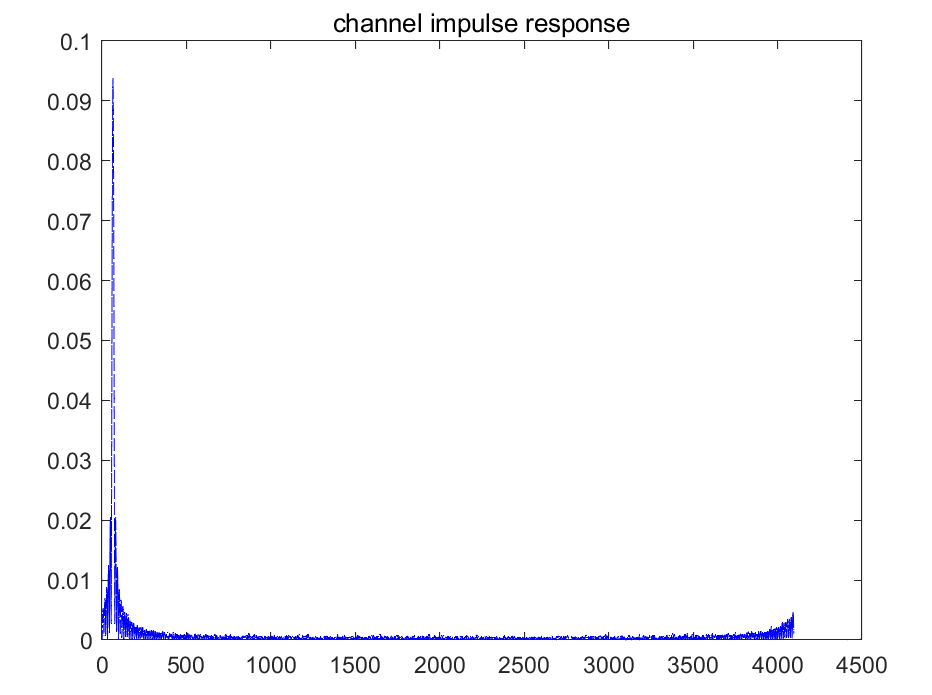
图3 DMRS相关峰值
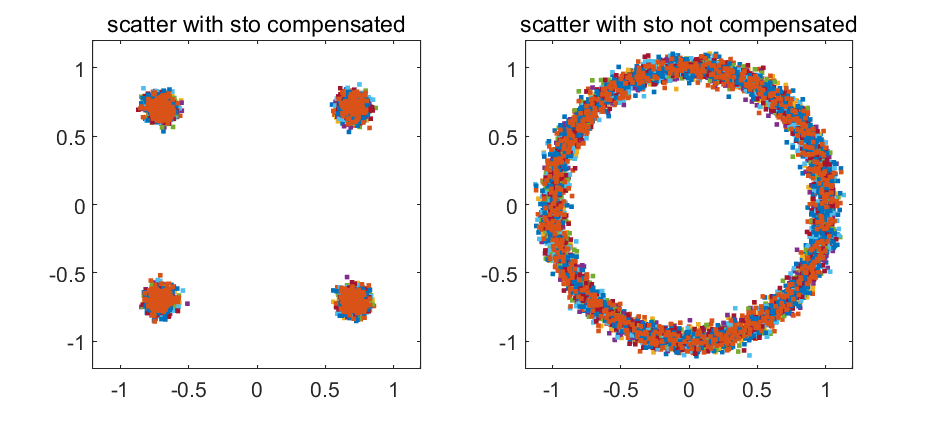
图4 STO补偿情况
这部分对应的Matlab代码如下,
% test_sto_est.m
% 3gpp ts38.211
clear,clc
close all
global ShowFigure;
ShowFigure=1;
rng(0);
Nfft = 4096; % FFT size
Ncp = 1024; % extended CP
Nofdm = Nfft+Ncp;
RB = 64; % resource block num
Qm = 2; % modulation order
Ebn0 = 20;
sto = 32;
Nsymb = 12;
dmrs_pos = [2,6,9];
Ng = Nfft-RB*12; % Guard
SNR = Ebn0+10*log10(Qm)+10*log10(RB*12/Nfft);
%% transmitter
b = pskmod(randi([0,3],RB*12,Nsymb-numel(dmrs_pos)),4,0.25*pi); % QPSK
dmrs = pskmod(randi([0,15],RB*6,numel(dmrs_pos)),16,0.125*pi);
% random number, not the real way for dmrs generation, just for simulation
tx_dmrs = dmrs./rms(dmrs,2);
% resource mapping
dmrs_idx = 1;
data_idx = 1;
x = zeros(RB*12,Nsymb);
for l = 1:Nsymb
if ismember(l,dmrs_pos)
x(:,l) = upsample(tx_dmrs(:,dmrs_idx),2); % configuration type 1 for pusch
dmrs_idx = dmrs_idx+1;
else
x(:,l) = b(:,data_idx);
data_idx = data_idx+1;
end
end
x1 = [zeros(Ng/2,Nsymb);x;zeros(Ng/2,Nsymb)];
x_tx = ifft(fftshift(x1,1));
x_tx = [x_tx(Nfft-Ncp+1:Nfft,:);x_tx]; % add CP
%% channel
% x_ch = x_tx;
x_ch = awgn(x_tx,SNR,'measured');
% y_rx = x_ch(Ncp+1:Nofdm,:); % remove cp without sto
y_rx = x_ch(Ncp+1-sto:Nofdm-sto,:); % with sto
%% receiver
y = fftshift(fft(y_rx),1);
yb = y(Ng/2+1:Ng/2+RB*12,:);
dmrs_idx = 1;
data_idx = 1;
rx_dmrs = zeros(RB*12,numel(dmrs_pos));
rx_data = zeros(RB*12,Nsymb-numel(dmrs_pos));
for l = 1:Nsymb
if ismember(l,dmrs_pos)
rx_dmrs(:,dmrs_idx) = yb(:,l);
dmrs_idx = dmrs_idx+1;
else
rx_data(:,data_idx) = yb(:,l);
data_idx = data_idx+1;
end
end
rx_dmrs = rx_dmrs(1:2:end-1,:);
sto_e = sto_est(rx_dmrs,tx_dmrs,Nfft,'freq');
% compensation for sto
k = Ng/2+[1:RB*12];
rx_data1 = rx_data.*exp(1i*(sto_e*2*pi/Nfft)*(k-1)');
if ShowFigure == 1
figure;
% set(0,'defaultfigurecolor','w');
subplot(121);
plot(rx_data1,'.'); axis equal;axis([-1.2,1.2,-1.2,1.2]);
title('scatter with sto compensated');
subplot(122);
plot(rx_data,'.'); axis equal;axis([-1.2,1.2,-1.2,1.2]);
title('scatter with sto not compensated');
end
其中,sto_est函数涵盖了多种估计算法,也在此处给出。
function varargout = sto_est(varargin)
% Symbol Timing Offset Estimation.
% sto = sto_est(y,xp,Nfft,'freq');
% sto = sto_est(y,Nfft,Ng,delay,'time');
% Inputs:
% y : received symbols in time domain or frequency domain.
% xp : transmitter pilot symbol in frequency domain.
% Nfft : FFT points.
% Ng : guard length.
% delay : delay length in time domain sto est.
% method : 'freq','time'
% Outputs:
% sto_est : STO estimation result.
global ShowFigure;
narginchk(1,5);
nargoutchk(0,2);
% parse input arguments.
lenargin = length(varargin);
if lenargin>=1
y = varargin{1};
method = 'time';
if lenargin >= 2
method = varargin{lenargin};
end
end
% estimate sto.
if strcmpi(method,'freq')
xp = varargin{2};
Nfft = varargin{3};
corr = conj(xp).*y;
corrt = ifft(corr,Nfft);
if ShowFigure == 1
figure; plot(abs(corrt),'b-.');
title('channel impulse response');
end
[~,pos] = max(corrt);
sto_est = (pos-1)/2;
sto_est = mean(sto_est);
% sto_est = (pos-1)/2*(Nfft/Nfft_sto); % lower FFT size for resource;
elseif strcmpi(method,'time')
Nfft = varargin{2};
Ng = varargin{3};
if lenargin == 5
delay = varargin{4};
else
delay = (Nfft+Ng)/2;
end
Nofdm=Nfft+Ng; minimum=100; sto_est=0;
Mag = zeros(1,Nofdm);
for n=1:Nofdm
nn = n+delay+[0:Ng-1]; tmp0 = abs(y(nn))-abs(y(nn+Nfft));
Mag(n) = sum(abs(tmp0).^2); % Squared difference
if Mag(n)<minimum
minimum=Mag(n);
sto_est=delay+(n-1)-Nfft-Ng;
end
end
end
% arguments out.
if nargout == 1
varargout = {sto_est};
elseif nargout == 2
varargout = {sto_est,0};
end
时域STO估计
基于CP的时域STO估计
该种估计技术主要是利用OFDM系统的CP信息。如图5所示,是使用双滑动窗口的时域STO估计技术示意图。
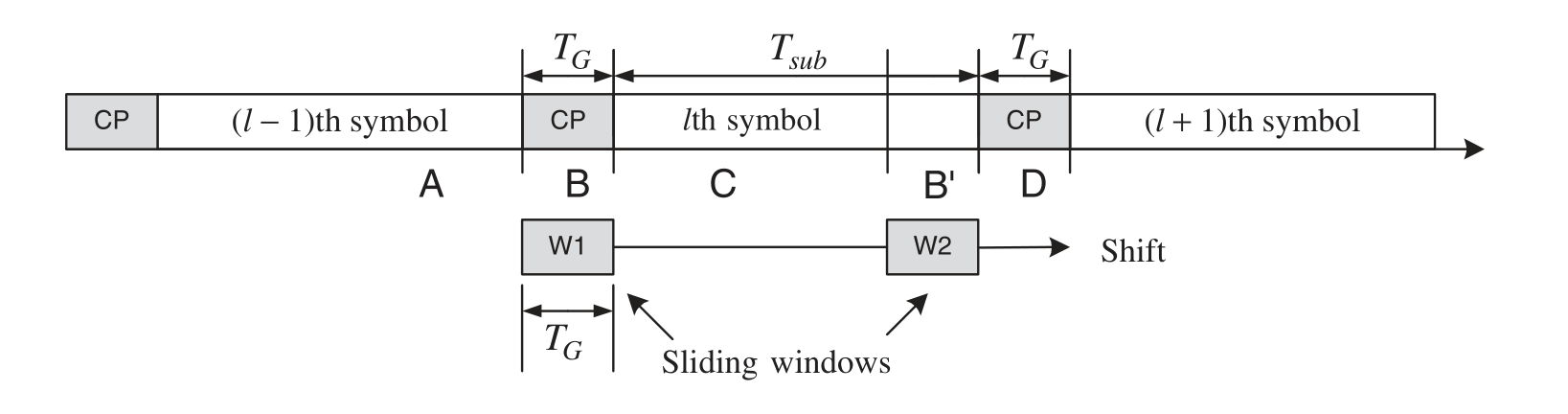
图5 时域STO估计,双滑动窗口
W1和W2是两个等长的滑动窗口,间隔距离等于OFDM符号长度。我们知道,循环前缀是把尾部特定长度复制到头部,那么,当W1恰好覆盖到循环前缀,W2此时覆盖的内容与W1完全相同,此时二者的区别最小。
判断二者区别最小的方法有很多种,比如差值最小,差值的平方最小,相关值最大等等,用公式分别表示为:
-
差值最小
\[\hat{\delta}=arg\quad \mathop{min}\limits_{\delta}\{\sum_{i=\delta}^{N_G-1+\delta} |y_l[n+i]-y_l[n+N+i]|\} \] -
差值平方最小
\[\hat{\delta}=arg\quad \mathop{min}\limits_{\delta}\{\sum_{i=\delta}^{N_G-1+\delta} (|y_l[n+i]-y_l[n+N+i]|)^2\} \] -
相关值最大
\[\hat{\delta}=arg\quad \mathop{max}\limits_{\delta}\{\sum_{i=\delta}^{N_G-1+\delta} |y_l[n+i]\cdot y_l^*[n+N+i]|\} \]
这里MATLAB仿真使用第2种,差值平方最小,得到的估计值与频域估计结果相同。代码参见频域估计的sto_est函数。
基于训练序列的时域STO估计
与基于CP的估计类似, 基于训练序列的时域STO估计也是利用已知的时域特性来估计STO。训练序列(Training Symbol)与导频类似,是在发射端发送的用来解调的参考信号。训练序列与导频的区别是,导频有多种插入方式,例如块状导频(Block Pilot),梳状导频(Comb Pilot),栅状导频(Lattice Pilot),如图6所示(图片来自《MIMO-OFDM Wireless Communications with MATLAB》6.1节)[1:1]。

图6 三种导频插入方式
后两者的插入方式,可以将导频信息散入到整个帧当中,而训练序列更类似与块状导频,单独占用一个符号用于接收机的同步。在3GPP TS38.211 6.4.1.1.3当中,如果传输预编码启用,PUSCH的DMRS信号插入方式为,隔1个符号插一个0(2倍上采样),反映在时域就是,重复一段。从公式的角度看一下:
其中,\(X'(k)\) 是\(X(k)\)的2倍上采样,\(x'(n)\) 和 \(x(n)\) 分别是2倍上采样和原序列的时域结果,当\(n=0:N-1\),\(x'(n)=x(n)\),当\(n=N:2N-1\),由于单位圆的周期性,此时\(x'(n)\)是前一段的重复。其在时域上的示意图如图7所示。
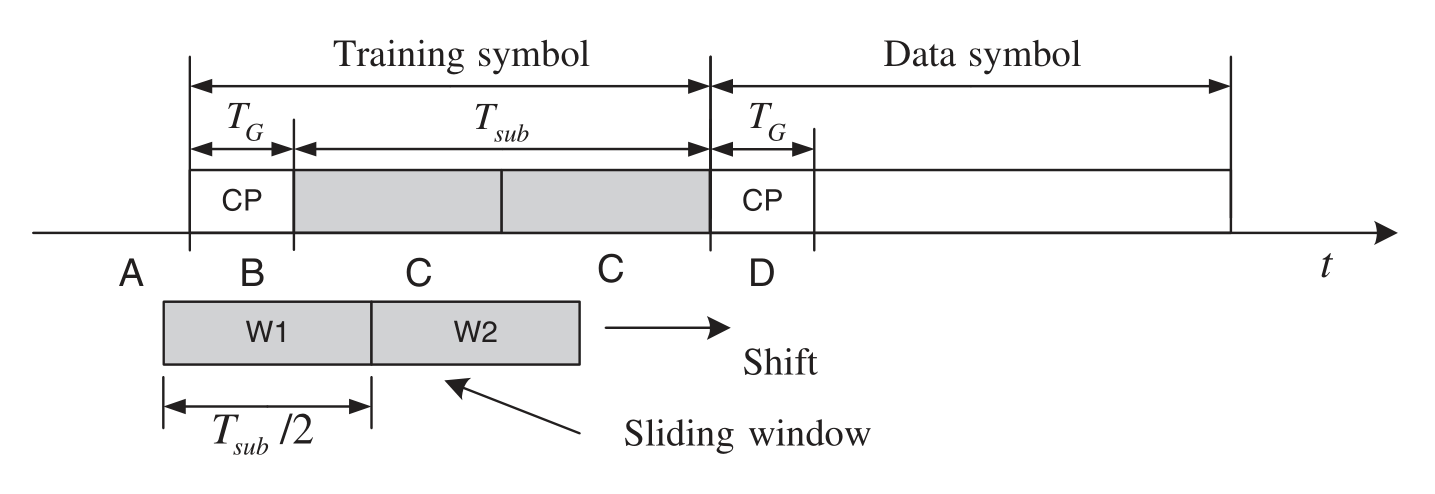
图7 时域STO估计,基于训练序列
基于训练序列的时域STO估计与基于CP的估计类似,只是原来的CP换成了时域上重复的训练序列,这里不再赘述。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号