【转载】费舍尔信息矩阵及自然梯度法

原文地址：

https://zhuanlan.zhihu.com/p/228099600

==============================================

费舍尔信息矩阵（Fisher Information Matrix, FIM）

假设我们有一个参数为向量 $θ$ 的模型，它对分布 $p(x|θ)$ 建模。在频率派统计学中，我们学习 $θ$ 的方法是最大化 $p(x|θ)$ 与参数 $θ$ 的似然（likelihood）。为了评估我们对 $θ$ 估计的好坏，我们定义了一个评分函数(score function)：

$s(θ)=∇_{θ}\log p(x|θ),$

评分函数即为对数似然函数的梯度。以下关于评分函数的结果是我们讨论的重要基础。

声明：我们模型的评分期望值为零。

证明. 以下对 $θ$ 求梯度

$\begin{align} \mathop{\mathbb{E}}\limits_{p(x|\theta)} [s(\theta)] &= \mathop{\mathbb{E}}\limits_{p(x|\theta)} [\nabla\log p(x|θ)]\\ &=\int\nabla\log p(x|θ)p(x|θ)\mathrm{d}x\\ &=\int \frac{\nabla p(x|θ)}{ p(x|θ)} p(x|θ) \mathrm{d}x\\ &=\int \nabla p(x|θ) \mathrm{d}x\\ &=\nabla \int p(x|θ) \mathrm{d}x\\ &= \nabla 1 \\ &= 0 \end{align}\\$

但是我们对我们的估计值有多大的把握呢？我们可以围绕估计值的期望，根据模型评分的协方差，定义一个不确定性度量。根据上式的结果：

$\mathop{\mathbb{E}}\limits_{p(x|\theta)} [(s(\theta)-0)(s(\theta)-0)^{\mathrm{T}}].$

那么，我们可以把它看作是一种信息。上面评分函数的协方差就是费舍尔信息的定义。由于我们假设 $θ$ 是一个向量，所以费舍尔信息是以矩阵形式存在的，称为费舍尔信息矩阵（FIM）：

$\mathrm{F} = \mathop{\mathbb{E}}\limits_{p(x|\theta)} [\nabla\log p(x|θ)\nabla\log p(x|θ)^{\mathrm{T}}].$

然而，通常我们的似然函数是复杂的，很难计算期望值。我们可以用经验分布 $\tilde{q}(x)$ 来近似 $\mathrm{F}$ 中的期望值，它由我们的训练数据 $X = \left\{ x_{1}, x_{2}, \cdots ,x_{N}\right\}$ 给出。在这种形式下， $\mathrm{F}$ 被称为经验费舍尔：

$\mathrm{F}=\frac{1}{N}\sum_{i=1}^{N}p(x_{i}|\theta)\nabla\log p(x_{i}|θ)\nabla\log p(x_{i}|θ)^{\mathrm{T}}.$

费舍尔信息矩阵与黑森（Hessian）矩阵的联系

$\mathrm{F}$ 有一个不是很明显的属性，它可以理解为，模型对数似然的黑森矩阵期望的负值。

声明：对数似然的负期望黑森，等于费舍尔信息矩阵 $\mathrm{F}$ 。

证明. 对数似然的黑森由其梯度的雅可比矩阵给出：

$\begin{align} {\mathop{\mathrm{H}}}_{\log p(x|\theta)} &=\mathrm{J}\left( \frac{\nabla\log p(x|θ)}{ p(x|θ)} \right) \\ &=\frac{{\mathop{\mathrm{H}}}_{p(x|\theta)}p(x|\theta)-\nabla p(x|θ) p(x|θ)^{\mathrm{T}}}{p(x|\theta)p(x|\theta)}\\ &=\frac{{\mathop{\mathrm{H}}}_{p(x|\theta)}p(x|\theta)}{p(x|\theta)p(x|\theta)} - \frac{\nabla p(x|θ) p(x|θ)^{\mathrm{T}}}{p(x|\theta)p(x|\theta)} \\ &= \frac{{\mathrm{H}}_{p(x|\theta)}}{p(x|\theta)} - \left( \frac{\nabla p(x|\theta)}{p(x|\theta)} \right){\left( \frac{\nabla p(x|\theta)}{p(x|\theta)} \right)}^{\mathrm{T}}, \end{align}\\$

其中，第二行使用了函数除法导数规则。对上述式子求期望，有：

$\begin{align} \mathop{\mathbb{E}}\limits_{p(x|\theta)}\left[ {\mathop{\mathrm{H}}}_{\log p(x|\theta)} \right]&= \mathop{\mathbb{E}}\limits_{p(x|\theta)} \left[\frac{{\mathrm{H}}_{p(x|\theta)}}{p(x|\theta)} - \left( \frac{\nabla p(x|\theta)}{p(x|\theta)} \right){\left( \frac{\nabla p(x|\theta)}{p(x|\theta)} \right)}^{\mathrm{T}}\right]\\ &=\mathop{\mathbb{E}}\limits_{p(x|\theta)}\left[ \frac{\mathrm{H}_{p(x|\theta)}}{p(x|\theta)} \right] -\mathop{\mathbb{E}}\limits_{p(x|\theta)}\left[ \left( \frac{\nabla p(x|\theta)}{p(x|\theta)} \right)\left( \frac{\nabla p(x|\theta)}{p(x|\theta)} \right)^{\mathrm{T}} \right]\\ &=\int \frac{\mathrm{H}_{p(x|\theta)}}{p(x|\theta)}p(x|\theta)\mathrm{d}x -\mathop{\mathbb{E}}\limits_{p(x|\theta)}\left[ \nabla \log p(x|\theta) \nabla \log p(x|\theta)^{\mathrm{T}} \right]\\ &=\mathrm{H}_{\int p(x|\theta) \mathrm{d}x}-\mathrm{F}\\ &=\mathrm{H}_{1}-\mathrm{F}\\ &=-\mathrm{F}. \end{align}$

故此， $\mathrm{F}=-\mathop{\mathbb{E}}_\limits{p(x|\theta)}\left[ \mathrm{H}_{\log p(x|\theta)} \right]$

费舍尔信息矩阵被定义为评分函数的协方差，它是一个曲率矩阵，可以理解为对数似然函数的黑森负期望。因此， $\mathrm{F}$ 的直接应用，是在二阶优化方法中替换 $\mathrm{H}$ 。

此外， $\mathrm{F}$ 与KL散度之间有着振奋人心的联系，就产生了自然梯度法。

自然梯度法（Natural Gradient Descent）

分布空间及KL散度

根据上文，我们有一个概率模型，用它的似然 $p(x|θ)$ 来表示，我们想最大化这个似然函数，找到最有可能的参数，等价的表述是最小化损失函数 $\mathcal{L}(θ)$ ，即负对数似然（negative log likelihood）

通常解决这个优化的方法是梯度下降法。在这种情况下，移动的方向由 $-∇_{θ} \mathcal{L}(θ)$ 给出。这是参数空间中，围绕当前 $θ$ 值的局部邻域，最陡峭的下降方向。形式上，我们有：

$\frac{-\nabla_{\theta}\mathcal{L}(\theta)}{\left \| \nabla_{\theta}\mathcal{L}(\theta) \right\|}= \lim_{\epsilon \rightarrow 0}{\frac{1}{\epsilon}} \mathop{\mathrm{arg\,min}}_{d\space \mathrm{s.t.} \space {\left \| d \right\|\leq\epsilon}} \mathcal{L}(\theta + d).$

上述表达式的意思是，在参数空间中最陡峭的下降方向上，选取一个向量 $d$ ，使得新参数 $θ+d$ 在当前参数 $θ$ 的 $ϵ$ 邻域范围内，且使得损失函数最小化。注意，这里采用欧式范数来表达邻域的情况。因此，梯度下降法的优化建立在参数空间的欧氏距离上。

然而，如果我们的目标是最小化损失函数（最大化似然），那么我们自然可以在所有可能由参数 $θ$ 实现的似然函数所构成的空间中进行移动。由于似然函数本身是一个概率分布，我们称这个空间为分布空间。因此，在这个分布空间，而不是参数空间中，采取最陡峭的下降方向，实际上对我们的优化更有意义。

那么在这个空间中我们需要使用哪种度量方式来衡量不同似然函数之间的距离呢？一个常见选择是KL散度（KL-divergence）： $D_{\mathrm{KL}}(p(x) \| q(x)) = \int p(x) \ln \left( \frac{p(x)}{q(x)} \right) \mathrm{d}x$

KL散度衡量了两个分布的"紧密程度"。尽管KL散度是非对称的，因此不算是一个严格的距离函数，我们还是可以使用它。这是因为当 $d$ 趋近于零时，KL散度是渐进对称的。所以，在一个局部邻域内，KL散度是近似对称的。

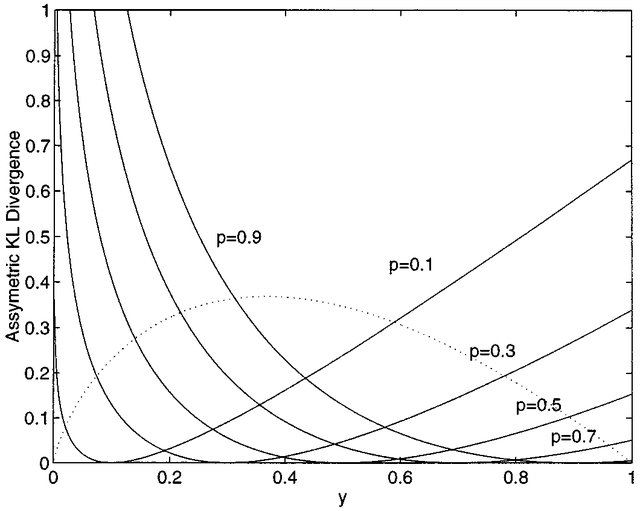
KL散度在概率小时上升更快，因此在p值较小时可以提供更好的概率估计

下图显示了在参数空间中使用欧氏距离时可能会遇到的问题。假设以下分布均为高斯分布，且均值在-2和2，一幅图中分布的方差为2，另一幅图中分布的方差为0.5：

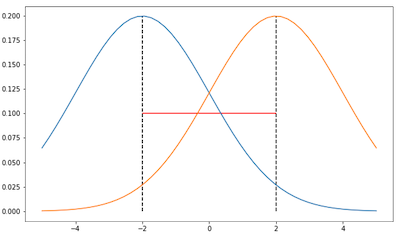
在两图中，根据欧氏距离（红色线段），两幅图中高斯分布的距离是相同的，也就是4。然而，如果考虑到高斯分布的形状，在第一幅图和第二幅图中，两个分布的“紧密度”明显是不同的，所以在分布空间中，它们的距离应该不同。在第一幅图中，两个分布的KL散度应该更低，因为它们曲线下方重叠的部分比第二幅图中两个分布的多。因此，如果只在参数空间中处理问题，就无法将由于参数本身导致的分布信息纳入考虑。

FIM和KL散度的关系

我们还需要回答一个问题：FIM和KL散度之间到底有什么联系？答案是，KL散度是分布空间的度量，而FIM定义了分布空间的局部曲率。

注：黑森矩阵本身就描述了函数的局部曲率

声明：两个分布 $p(x|θ)$ 和 $p(x|θ′)$ 之间，相对于 $θ′$ 的KL散度，在 $θ′=θ$ 时的黑森矩阵，即为费舍尔信息矩阵 $\mathrm{F}$ 。

证明. KL散度可以写成熵（entropy）和交叉熵（cross-entropy）两项，即：

$\mathrm{KL}\left[ p(x|\theta) \space || \space p(x|\theta ') \right] = \mathop{\mathbb{E}}_\limits{p(x|\theta)}\left[ \log p(x|\theta) \right] - \mathop{\mathbb{E}}_\limits{p(x|\theta)}\left[ \log p(x|\theta') \right]$

对 $\theta'$ 求一阶导：

$\begin{align} \nabla_{\theta'}\mathrm{KL}\left[ p(x|\theta) || p(x|\theta') \right] &= \nabla_{\theta'}\mathop{\mathbb{E}}_\limits{p(x|\theta)}\left[ \log p(x|\theta) \right] - \nabla_{\theta'}\mathop{\mathbb{E}}_\limits{p(x|\theta)}\left[ \log p(x|\theta') \right]\\ &= -\mathop{\mathbb{E}}_\limits{p(x|\theta)}\left[\nabla_{\theta'} \log p(x|\theta') \right]\\ &= - \int p(x|\theta) \nabla_{\theta'} \log p(x|\theta')\mathrm{d}x. \end{align}$

第一步第一项里面没有 $θ′$ ，所以为0

对 $\theta'$ 求二阶导：

$\begin{align} \nabla^{2}_{\theta'}\mathrm{KL}\left[ p(x|\theta) || p(x|\theta') \right] &= - \int p(x|\theta) \nabla^{2}_{\theta'} \log p(x|\theta')\mathrm{d}x. \end{align}$

因此，相对于 $θ′$ 的KL散度，在 $θ′=θ$ 时的黑森矩阵为：

$\begin{align} \mathrm{H}_{\mathrm{KL}\left| p(x|\theta)\|p(x|\theta') \right|} &= - \int p(x|\theta) \nabla^{2}_{\theta'} \log p(x|\theta')|_{\theta'=\theta}\mathrm{d}x\\ &=-\int p(x|\theta)\mathrm{H}_{\log p(x|\theta)}\mathrm{d}x\\ &=-\mathop{\mathbb{E}}_{p(x|\theta)}\left[ \mathrm{H}_{\log p(x|\theta)} \right]\\ &= \mathrm{F}. \end{align}$

最后一步请参见上方第二部分“FIM与黑森矩阵的联系”的结论。

分布空间的最速下降法

现在我们准备使用FIM来改进梯度下降法。
首先，我们需要推导出KL散度在 $θ$ 处的泰勒展开。

声明：当 $d→0$ 时，KL散度的二阶泰勒展开为 $\begin{align} \mathrm{KL}\left[ p(x|{\theta}) \| p(x|\theta + d) \right] &\approx \frac{1}{2}d^{\mathrm{T}}\mathrm{F}d. \end{align}$

证明. 根据定义，KL散度的二阶泰勒数列展开为：

$\begin{align} \mathrm{KL}\left[ p(x|{\theta}) \| p(x|\theta + d) \right] &\approx \mathrm{KL}\left[ p(x|{\theta}) \| p(x|\theta) \right]+(\nabla_{\theta'}\mathrm{KL}\left[ p(x|{\theta}) \| p(x|\theta') \right]|_{\theta = \theta'})^{\mathrm{T}}d+\frac{1}{2}d^{\mathrm{T}}\mathrm{F}d\\ &=\mathrm{KL}\left[ p(x|{\theta}) \| p(x|\theta) \right] - \mathop{\mathbb{E}}_\limits{p(x|\theta)}\left[\nabla_{\theta} \log p(x|\theta) \right]^{\mathrm{T}}d+\frac{1}{2}d^{\mathrm{T}}\mathrm{F}d \end{align}$

第一项中的两个分布都是 $p(x|\theta)$ ，所以KL散度为0
第二项中，对数似然函数的梯度的期望（也就是上面证明过程中KL散度的梯度），已在本文第一个声明中被证明为0

因此必须展开到二阶

因此，唯一剩下的项就是 $\frac{1}{2}d^{\mathrm{T}}\mathrm{F}d$

其次，我们想求分布空间中，使损失函数 $\mathcal{L}(θ)$ 最小化的更新向量 $d$ ，这样就可以知道在哪个方向上KL散度减少得最快。这个操作类似于最速下降法，但是在分布空间以中KL散度为度量，而不是通常情况下在参数空间中以欧氏距离为度量。对 $d$ 的要求可以写成：

$\begin{align} d^{*} &= \mathop{\mathrm{arg\,min}}_{d \space s.t. \space \mathrm{KL\left[ p(x|{\theta}) \| p(x|\theta + d) \right] = \epsilon }} \mathcal{L}(\theta+d), \end{align}$

其中 $\epsilon$ 是某个常数。将KL散度固定为某个常数的目的，是为了确保不管曲率如何，参数都以恒定的速度在分布空间中移动，这使得算法对模型的更新更加稳健，即算法不关心模型本身引发的参数改变，它只关心参数改变引起的分布变化。

如果将 $d^{*}$ 写成拉格朗日算子的形式，并用二阶泰勒序列展开逼近约束条件中的KL散度，用一阶泰勒展开逼近 $\mathcal{L}(θ+d)$ ：

$\begin{align} d^{*} &= \mathop{\mathrm{arg\,min}}_{d} \mathcal{L}(\theta+d) + \lambda(\mathrm{KL}\left[ p(x|{\theta}) \| p(x|\theta + d) \right] - \epsilon )\\ &\approx \mathop{\mathrm{arg\,min}}_{d} \mathcal{L}(\theta) + \nabla_{\theta} \mathcal{L}(\theta)^{\mathrm{T}}d+\frac{1}{2} \lambda d^{\mathrm{T}}\mathrm{F}d-\lambda \epsilon \end{align}$

为求得最小值，我们求它对 $d$ 导数为0时方程的解：

$\frac{\partial}{\partial d}\left( \mathcal{L}(\theta) + \nabla_{\theta} \mathcal{L}(\theta)^{T}d + \frac{1}{2} \lambda d^{T} \mathrm{F}d-\lambda \epsilon \right) = 0 \\ \nabla_{\theta} \mathcal{L} (\theta) + \lambda \mathrm{F} d = 0 \\ \lambda \mathrm{F} d = - \nabla_{\theta} \mathcal{L} (\theta) \\ d = - \frac{1}{\lambda} \mathrm{F}^{-1} \nabla_{\theta} \mathcal{L}(\theta)$

只要系数 $\frac{1}{λ}$ 是常数（可以将它吸收到学习率中），就可以得到最优下降方向，即考虑以 $\mathrm{F}^{-1}$ 定义局部曲率的分布空间中，梯度的相反方向。在此，我们得到了自然梯度（Natural Gradient）和自然梯度法（Natural Gradient Descent）的定义：

定义：自然梯度被定义为 $\tilde{\nabla}_{\theta} \mathcal{L}(\theta) = \mathrm{F}^{-1} \nabla_{\theta} \mathcal{L} (\theta).$

学习率：我们将KL散度固定为常数的限制单独写出来

$\mathrm{KL\left[ p(x|{\theta}) \| p(x|\theta + d) \right]} \approx \frac{1}{2}\left( \theta - \theta' \right)^{\mathrm{T}}\mathrm{F}\left( \theta - \theta' \right) = \epsilon$

由于在实际训练时，梯度 $g$ 是通过使用在参数 $\theta$ 的情况下采样模拟的分布而计算出来的，我们将其记为 $\hat{g}$ ，上面的等式可以转写为：

$\frac{1}{2}\left( \alpha \hat{g} \right)^{\mathrm{T}}\mathrm{F}\left( \alpha \hat{g} \right) = \epsilon$

解得 $\alpha = \sqrt{\frac{2 \epsilon}{\hat{g}^{\mathrm{T}}\mathrm{F} \hat{g}}}$

算法：自然梯度法

Repeat:
    对模型进行正向传播，计算损失L(θ)
    计算梯度g = ∇θL(θ)
    计算Fisher信息矩阵F，或其相对于训练数据的经验版本
    计算自然梯度
    更新参数：θ=θ- α自然梯度，其中α是学习率。
Until 收敛

即 $\theta_{k+1} = \theta_{k} + \sqrt{\frac{2 \epsilon}{\hat{g_{k}}^{\mathrm{T}}\mathrm{F} \hat{g_{k}}}} \mathrm{F}^{-1} \hat{g_{k}} , \mathrm{for} \space k = 0, 1, 2, \cdots$

--------------------------------------------------

posted on 2021-03-26 13:32 Angry_Panda 阅读(1370) 评论(0) 编辑收藏举报

刷新页面返回顶部

Angry Panda

【转载】费舍尔信息矩阵及自然梯度法