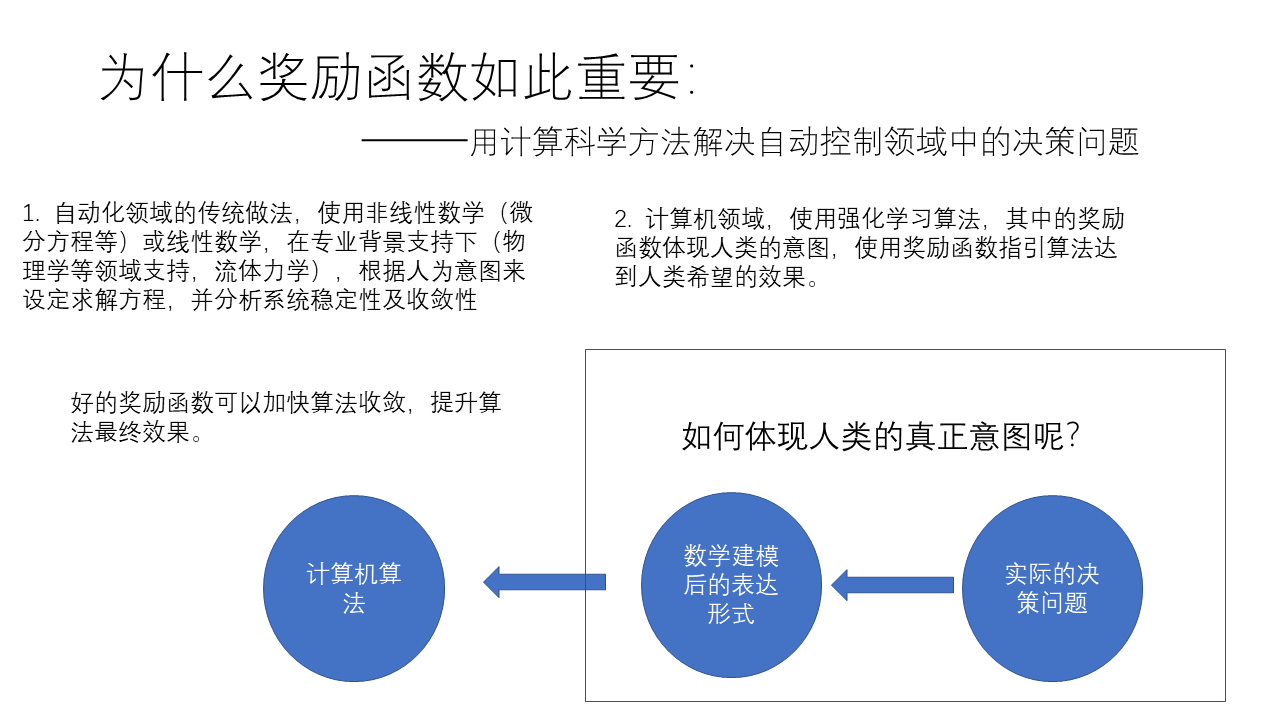
论文《policy-gradient-methods-for-reinforcement-learning-with-function-approximation 》的阅读——强化学习中的策略梯度算法基本形式与部分证明

最近组会汇报，由于前一阵听了中科院的教授讲解过这篇论文，于是想到以这篇论文为题做了学习汇报。论文《policy-gradient-methods-for-reinforcement-learning-with-function-approximation 》虽然发表的时间很早，但是确实很有影响性，属于这个领域很有里程牌的一篇论文，也是属于这个领域的研究者多少应该了解些的文章。以下给出根据自己理解做成的PPT。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---------------------------------------------------------------------------------

 

 

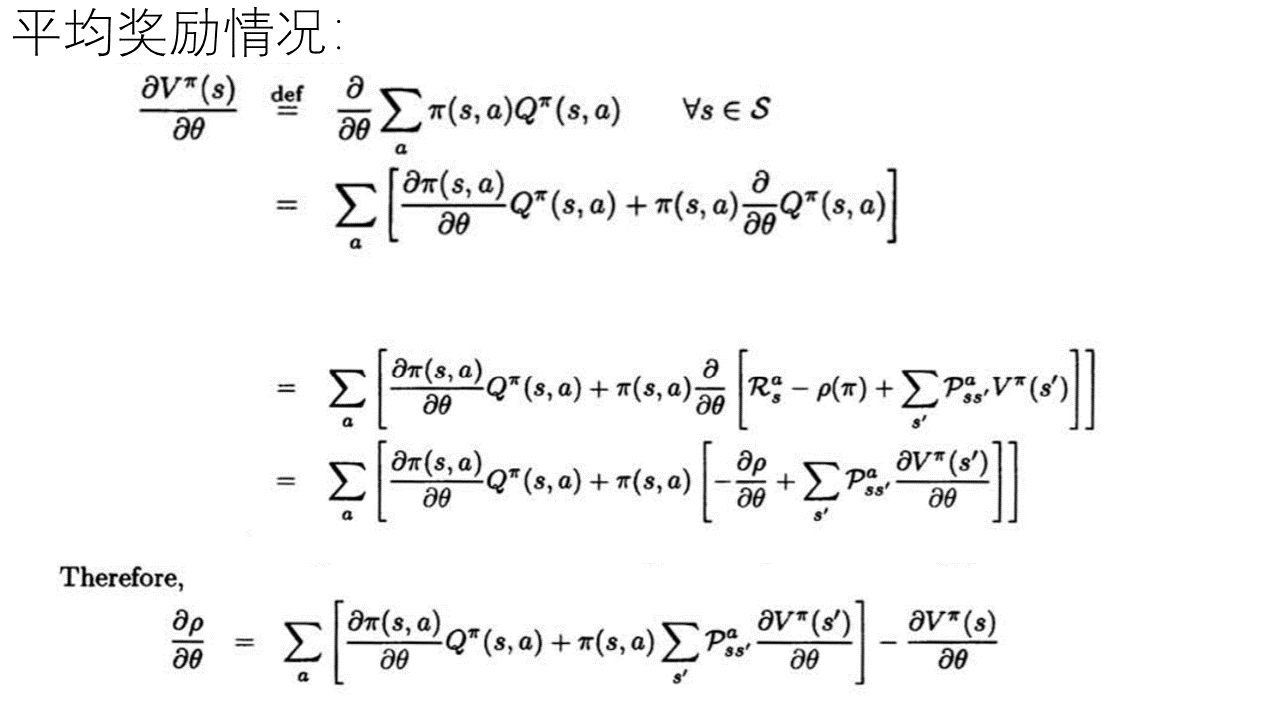
后注：

 

其实，很多人觉得这个推导就是多此一举，这个公式和证明根本没有必要，因为这个公式本身就是显而易见的，原因如下：

 

已知（根据MDP及强化学习的定义有）：

公式（1）：

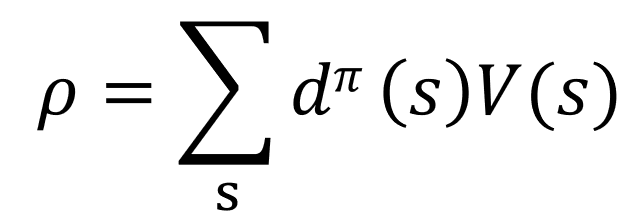
公式（2）：

 

 

 

 

而上面的这篇论文通篇要做的就是下面的公式成立，并且满足逼近函数f为向量且上面的公式（4）及step_size的要求可以收敛到局部最优：

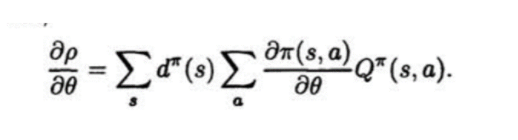
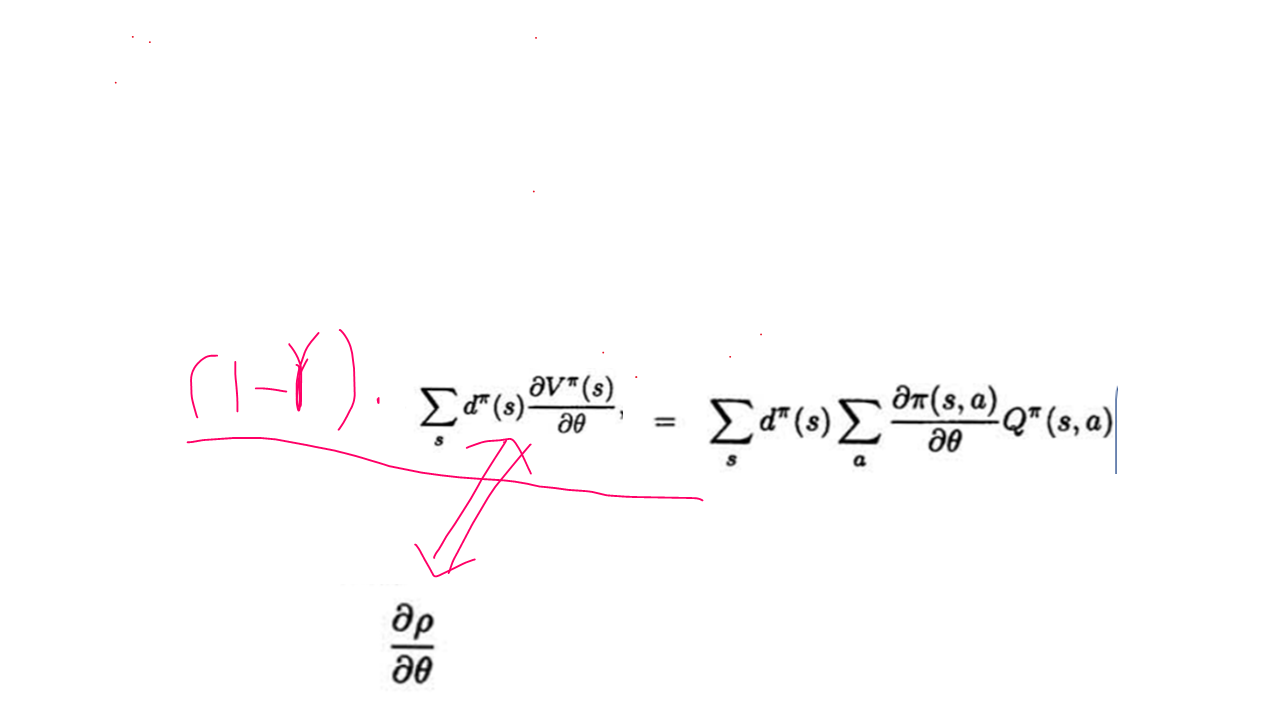
根据后注中的公式（1）和（2），不是直接就可以得到论文中的这个公式嘛，而且而这个公式必然在理想条件下收敛（对整体环境有很好的抽样的情况下），那么把Q换成逼近函数f ，不是也会收敛的嘛，又何必费力去推导最后还得到一个在多个条件下收敛到局部解的结论，这不是显而易见的事情还非得花无用功去为了推导公式而去推导公式和证明收敛的吗？

 

 

 

在此，回答一下  这方面的提问：

首先，要说的就是提出这个问题的人本身就忽略了下面的事情：

   与   本身都是对策略依赖的，或者说这两个item本身就含有策略参数θ  ， 所以根本就不存在由后注中的（1），（2）公式可以推导出论文的最终公式的形式。

 

换句话说就是策略pi和Q 对策略参数θ来说都不是常数的，由此才有上面论文中的各种情况下的推导。

 

 

 

 

对于收敛的问题：

虽然我们可以知道在完全抽样的情况下策略梯度用策略和Q来表示是收敛的，都是实际Q并不知道，我们需要用函数近似和采样的方法来获得，而在这样的整个动态的学习过程中即要优化策略梯度的参数，又要优化近似函数f的参数，而这样的情况下是否收敛却并不知道的。

 

 如果在某个学习过程中 近似函数f 对 Q值的估计 过程收敛到局部最优，则有论文中的公式 （3）， 而在近似值函数f 和 策略函数pi 满足论文中的公式（4），则有论文中的公式（5），（6），  在有对step_size的限制下才有 满足以上条件的值函数近似策略梯度算法收敛都局部最优的结论。

 

 

 

---------------------------------------