计算机科学采用训练数据集,验证数据集,测试数据集 的方法 为什么不采用统计学中常用的假设检验呢? (参数检验 和 非参数检验)
如题所说, 这个问题作为一个本科读管理,硕士读计算机却旁修经济学,博士在读计算机的我来说感觉比较迷惑的。在管理学,经济学,计算机这三门学科在解决优化问题的时候采用的方法大致相同,其核心都是统计学,管理学,计算机科学中采用的基础方法,如线性回归,多元线性回归,广义线性回归,决策树,SVM,ID3,KNN等分类方法,同时也包括遗传算法,模糊数学,粒子群算法等, 这时候我们会发现这样一个情况就是 以经济学为代表对数据进行回归预测是一定要采取假设检验来看最终的P值,判断模型是否成立,这一步是必须的操作,对于数据的平稳性的验证等,但是在计算机学科中却极少见到这样的操作,我在读硕士期间曾做过智能算法方向的学习,在这里有见过比较少的部分采用了假设检验,但是这就出现了一个比较神奇的问题,那就是不同学科采用同样方法来解决问题时问什么经济学等学科就要采用假设检验,而计算机学科却极少的采用建设检验呢?
===============================================================
以下线内内容引自:
https://www.cnblogs.com/sanshuiyijing/p/3447315.html
百度百科的定义:
非参数检验(Nonparametric tests)是统计分析方法的重要组成部分,它与参数检验共同构成统计推断的基本内容。参数检验是在总体分布形式已知的情况下,对总体分布的参数如均值、方差等进行推断的方法。但是,在数据分析过程中,由于种种原因,人们往往无法对总体分布形态作简单假定,此时参数检验的方法就不再适用了。非参数检验正是一类基于这种考虑,在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。由于非参数检验方法在推断过程中不涉及有关总体分布的参数,因而得名为“非参数”检验。
单样本:
SPSS单样本非参数检验是对单个总体的分布形态等进行推断的方法,其中包括卡方检验、二项分布检验、K-S检验以及变量值随机性检验等方法。
独立样本:
两独立样本的非参数检验
相关样本:
=================================================================
说实话,上一个引自的线内内容有些看不懂,设计到统计学的东西一般都不是很好懂,给出下面的资料,
引自:https://zhidao.baidu.com/question/61729761.html
两独立样本的非参数检验是在对总体分布不甚了解的情况下,通过对两组独立样本的分析来推断样本来自的两个总体的分布等是否存在显著差异的方法。独立样本是指在一个总体中随机抽样对在另一个总体中随机抽样没有影响的情况下所获得的样本。
1,参数检验是针对参数做的假设,非参数检验是针对总体分布情况做的假设,这个是区分参数检验和非参数检验的一个重要特征。
2,二者的根本区别在于参数检验要利用到总体的信息(总体分布、总体的一些参数特征如方差),以总体分布和样本信息对总体参数作出推断;非参数检验不需要利用总体的信息(总体分布、总体的一些参数特征如方差),以样本信息对总体分布作出推断。
3,参数检验只能用于等距数据和比例数据,非参数检验主要用于记数数据。也可用于等距和比例数据,但精确性就会降低。
非参数检验往往不假定总体的分布类型,直接对总体的分布的某种假设(例如如称性、分位数大小等等假设)作统计检验。当然,上一节介绍的拟合优度检验也是非参数检验。除了拟合优度检验外,还有许多常用的非参数检验。最常见的非参数检验统计量有 3类:计数统计量、秩统计量、符号秩统计量。
非参数检验(Nonparametric tests)
是统计分析方法的重要组成部分,它与参数检验共同构成统计推断的基本内容。非参数检验是在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。由于非参数检验方法在推断过程中不涉及有关总体分布的参数,因而得名为“非参数”检验。
但是,在数据分析过程中,由于种种原因,人们往往无法对总体分布形态作简单假定,此时参数检验的方法就不再适用了。非参数检验正是一类基于这种考虑,在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。
二者的根本区别
在于参数检验要利用到总体的信息(总体分布、总体的一些参数特征如方差),以总体分布和样本信息对总体参数作出推断;非参数检验不需要利用总体的信息(总体分布、总体的一些参数特征如方差),以样本信息对总体分布作出推断。
参数检验只能用于等距数据和比例数据,非参数检验主要用于记数数据。也可用于等距和比例数据,但精确性就会降低。
拓展
参数检验,是数理统计学中根据一定假设条件由样本推断总体的一种方法。具体作法是:根据问题的需要对所研究的总体作某种假设,记作H0;选取合适的统计量,这个统计量的选取要使得在假设H0成立时,其分布为已知;由实测的样本,计算出统计量的值,并根据预先给定的显著性水平进行检验,作出拒绝或接受假设H0的判断。常用的假设检验方法有U检验法、T检验法、χ2检验法(卡方检验)、F检验法等。
参数假设检验又称统计假设检验,是一种基本的统计推断形式,也是数理统计学的一个重要的分支,用来判断样本与样本,样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征作出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作出推断。
=====================================================
下图引自:
https://blog.csdn.net/xiaodongxiexie/article/details/72084946

这个说的应该是参数假设检验。
=====================================================
根据上面的资料,个人的一些观点是,统计学中的参数假设检验是在总体分布函数的形式是已知的,只不过对总体分布函数中的参数是未知的情况, 但是在计算机学科中我们所面对的问题首先就是在整体分布形式未知的情况下来进行的,比如推荐算法,我们可能永远都不会知道每个用户所喜欢商品的分布,在分类问题中谁又能知道下面这个东西的分布:
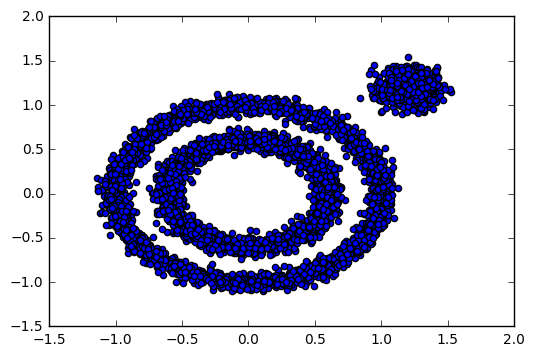
也就是说在计算机学科中我们所面对的大量问题难以将整体的分布用一个统计模型来表示(带参数的统计模型)。如果这个模型是可以被统计模型表示的话,那么有两种情况在计算机学科中,一种是生成式方法,一种是判别式方法, 生成式方法本身就不采用统计模型来处理(若贝叶斯方法),判别式方法中有一些也不采用统计模型若SVM等,但是判别式方法中有一些是采用统计模型的,如线性回归和logistics回归,那么它们为什么不采用假设检验来验证呢?
以下说的是我自己的理解:
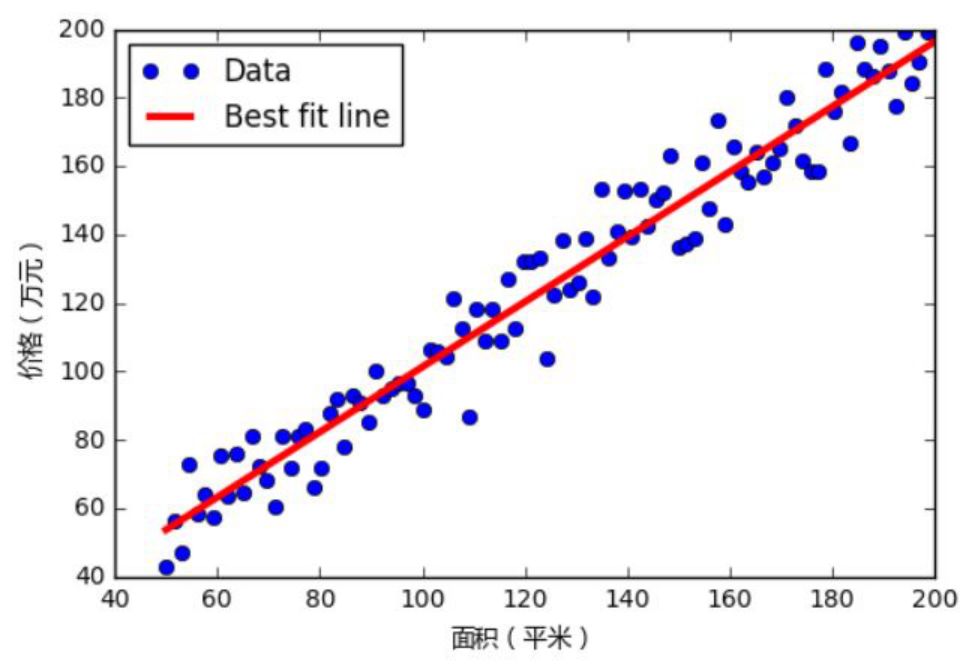
首先, 数据量上的问题,经济学等学科 30个数值以上就已经算是大数据了,可以看出大部分的情况下数据是远小于30的,一般10个多一些的比较常见,这种情况下该抽样数据是否能够表征整体分布是存在问题的, 这些抽样数据可以用线性表示,也可能可以用非线性表示,如下图:

而计算机学科所面对的问题 抽样数据都比较多,在某种程度上可以表征整体,如下图:
其次, 在计算机学科中是否抽样的数据,即训练数据就一定是符合某个统计模型呢(线性或曲线回归),这个也是可能不一定的,如下图:
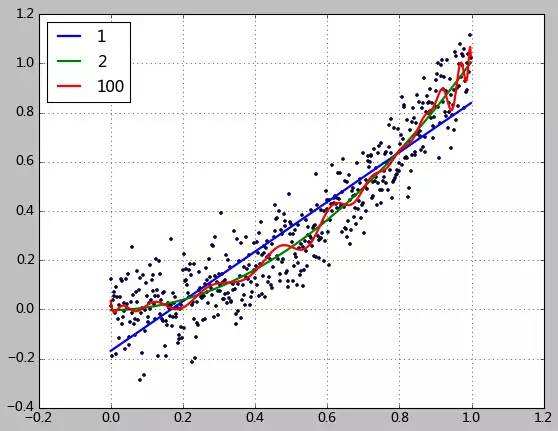
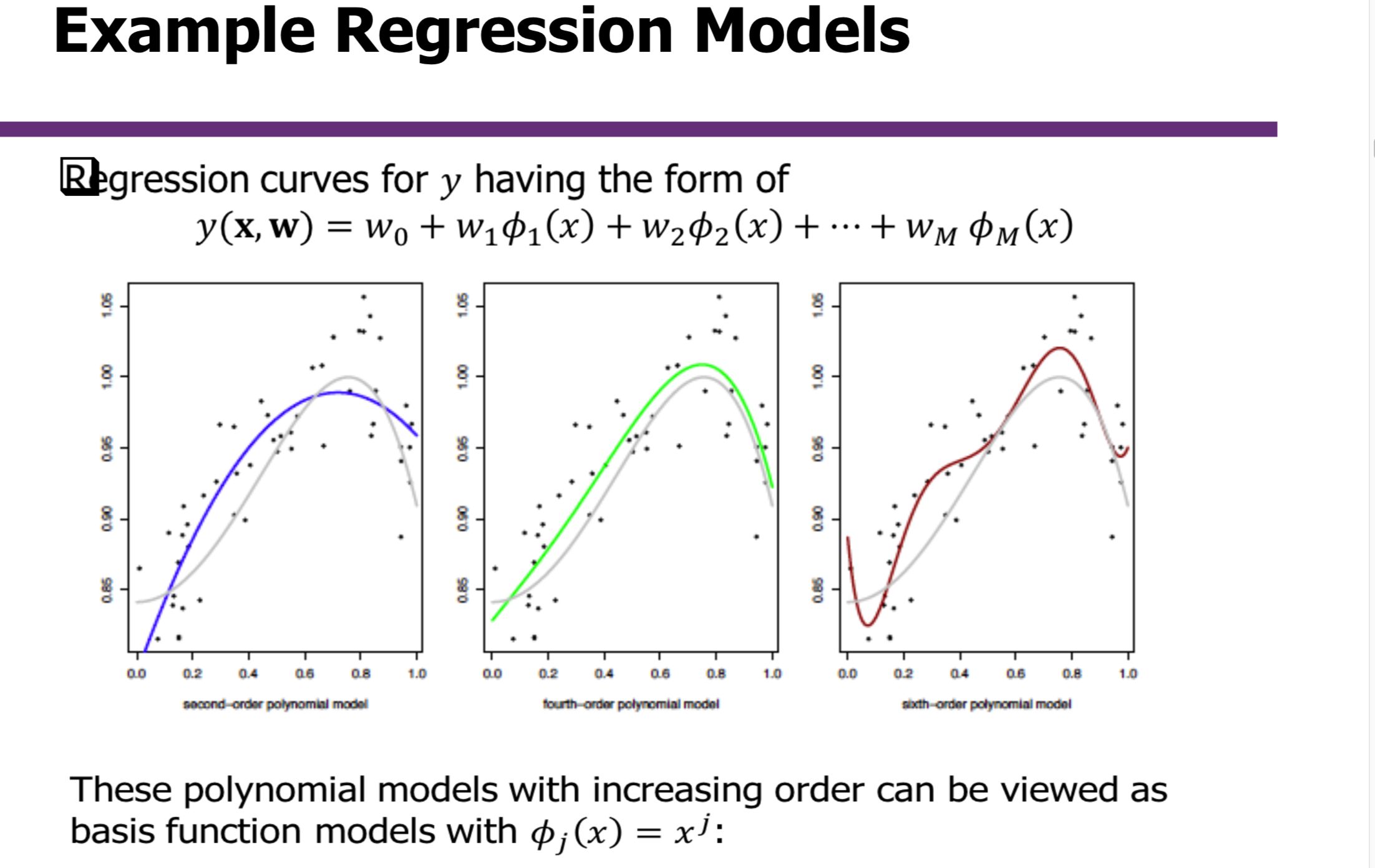


可以看出在计算机学科中(特指机器学习)所面对的问题也并不是只采用统计模型就能很好的解决问题的,这个问题貌似和上个问题一样,其实不然,上一个说的是机器学习中遇到这样情况比较少,而这里说的是一旦遇到的时候。
个人观点是:统计学中模型一旦固定,剩下的就是推导,得出参数的方程式,根据抽样数据计算出参数值大小。但是统计模型的建立本身是在多种假设之上的,其中之一就是残差服从正态分布等。而在计算机学科中的机器学习往往并不假设这些,它会根据不同的模型方法来构建模型,然后设置损失函数,用梯度下降法求解,最终的目标是在一堆模型中找出一个最好的方法(这其中可能包括线性回归、曲线回归等,如上面 四个sin图所示),我们的目标是寻找出一个拟合性更强的模型,并使其泛化性更强,这样所求解出的回归模型对整体的表征最强,其实这其中并没有用到统计模型也没有什么过多的假设,因此也就自然么有假设检验一说了。
非参数假设检验直接就不用考虑了,因为它是无参数的,计算机学科中要解决的问题是根据抽样的信息来推断出整体的分布或近似分布(生成式方法),也或者是某种判别方法,生成方法我们是要有对整体分布的一个参数表示的, 判别方法中也是需要用参数表示的。
===================================================================
总结一句:非参数假设检验不对问题进行参数估计,因此在计算机学科中基本不用,或者较少使用,因为它对估计模型意义不大。
计算机学科中能使用到统计模型的地方一般是判别式的分类方法,主要是线性回归,这时候不使用统计中的参数假设检验是因为计算机学科求解问题的具体情况不同(数据量不同),解决时采用的具体方法不同(统计学中使用统计模型推导出 参数的方程式, 计算机学科中采用损失函数和梯度下降方法,不断参数空间中探索尝试以寻找最优参数,这部分其实已经不是在使用统计模型了);最终的求解目标不同,统计学中得出的结果比较严谨,在数据量较小或者整体模型和统计模型较接近的时候可能由于机器学习的方法,而且在统计中我们是不确定那些属性是对模型有用的,模型是否平稳等问题,本身统计学中属性较少,属性选择的不好可能很大程度音响最终的结果,而在机器学习中采用损失函数和梯度下降的方法受属性影响没有那么大,也包括平稳性;精度要求的不同,在统计学科中结果的严谨性往往是必须要保证的,而在机器学习中往往是试错探索寻找的过程,实在一些方法中找到一个更好的方法。
===========================
附加:
另外一个自己想到的问题,统计学更强调分析,也就是说它需要知道哪个变量对模型的影响最大,影响的幅度有多少,这几个变量属性之间是否相关,等等,这么说吧统计学的分析更强调定量的来分析模型,因为不同属性之间的性质对问题的研究也是十分的重要的,比如研究一个地方的财政税收,我们需要得出的是哪个属性对其有影响,像当地的人口基数,国企数量,私企数量,公路数量,年轻人口数量,评价受教育程度等等, 其中每个属性对问题的影响程度,各个属性之间是否关联,如果关联哪个属性更具有表征性,各个属性对模型的拟合结果影响程度有多少,可信度又有多少,等等, 而这些才是在统计学问题中真正关心的东西。 而在计算机科学中我们不关心属性之间的关系,也不关心各个属性对模型结果的影响程度,可信度有多少,总之一句话就是计算机学科要求的是模型可以 work , 只要可以 work 就好, 训练模型时候你给我 10000个训练个体,每个训练个体有100个属性,我们能够得出一个模型比其他常用的模型得出更准确的结果就好(这个是指拿新的例子来测试的时候,即测试集),这时候要求的是训练时候个体属性为100个,测试时候属性也要求是100个,得出的结果更准确模型就更好,至于每个属性对结果的影响程度,可信度都不是我们所考虑的。
总之,统计学侧重分析,即各个属性对模型的影响,并量化影响。而计算机学科更侧重结果,就是说我拿什么样的数据训练模型,然后再拿什么样的数据测试模型得出的结果更好,模型泛化更好就OK,这说明模型work了,至于哪个属性对模型更具有影响性,可信度为多少这方面我们统统不考虑,也正是这一点统计学在做模型的时候要种种假设都放在一起然后在一个比较理想的环境下得出模型结果,然后再反推回去看看假设是否成立, 而计算机学科在处理问题时基本没有这么多的假设,或者比较弱的假设,甚至根本就没有假设,它即没有假设又没有统计量,那它又何来的假设检验呢。这可能就是一个重分析,一个重是否work的区别吧。
posted on 2018-12-17 20:49 Angry_Panda 阅读(1183) 评论(1) 编辑 收藏 举报



