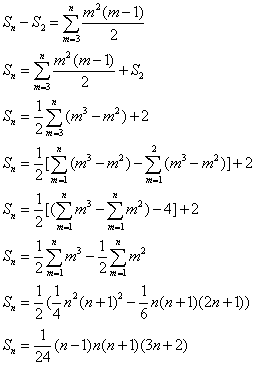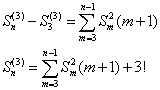有趣的阶乘

    先来看一道题目：10个数1,2,3…10两两乘积之和是多少？

    解：对于一般的数列求和，求前n项和的S_n的最高次幂为通项最高次幂加1，但此题非也，还应考虑项数，此题项数为C_n²，为关于n的二次幂形式，故此题的前n项和的S_n应为最高次幂为4的多项式。

    设：S_n为前n个自然数两两乘积之和，则n>=2

S₂=1×2=2

S₃=1×2+1×3+2×3=11

S₄=1×2+1×3+1×4+2×3+2×4+3×4=35

S₅=1×2+1×3+1×4+1×5+2×3+2×4+2×5+3×4+3×5+4×5=85

S₆=1×2+1×3+1×4+1×5+1×6+2×3+2×4+2×5+2×6+3×4+3×5+3×6+4×5+4×6+5×6=265

……

    通过观察不难发现：

S₃-S₂=(1+2)×3=3²(3-1)/2

S₄-S₃=(1+2+3)×4=4²(4-1)/2

S₅-S₄=(1+2+3+4)×5=5²(5-1)/2

S₆-S₅=(1+2+3+4+5)×6=6²(6-1)/2

……

S_n-S_n-1=[1+2+3+……+(n-2)+(n-1)]×n=n²(n-1)/2

    将等式两边相加得：

    所以S₁₀=1/24×9×10×32=1320

    推广：设S_n^(k)为前n个自然数kk相乘的乘积之和(n>=k)试求S_n^(k)表达形式

S₃⁽³⁾=1×2×3=3!=6

S₄⁽³⁾=1×2×3+1×2×4+1×3×4+2×3×4

       =1×2×3+(1×2+1×3+2×3)×4

       =S₃⁽³⁾+S₃⁽²⁾×4

S₅⁽³⁾=1×2×3+1×2×4+1×2×5+1×3×4+1×3×5+1×4×5+2×3×4+2×3×5+2×4×5+3×4×5

       =1×2×3+1×2×4+1×3×4+2×3×4+(1×2+1×3+1×4+2×3+2×4+3×4)×5

       =S₄⁽³⁾+S₄⁽²⁾×5

……

S_n⁽³⁾=S_n-1⁽³⁾+S_n-1⁽²⁾×n

    所以

S₄⁽³⁾-S₃⁽³⁾=S₃⁽²⁾×4

S₅⁽³⁾-S₄⁽³⁾=S₄⁽²⁾×5

S₆⁽³⁾-S₅⁽³⁾=S₅⁽²⁾×6

……

S_n⁽³⁾-S_n-1⁽³⁾=S_n-1⁽²⁾×n

    将左右两边相加得

    当m=2时,(m+1)S_m⁽²⁾=(2+1)×2!=3!,所以

    将S_m⁽²⁾=1/24(m-1)m(m+1)(3m+2)代入可求S_n⁽³⁾

    再由此递推公式可求：

    至此，S_n^(k)的递推公式求得，而通项是没有求出的，该问题只是一个铺垫，下面进入正题，我们来讨论n的阶乘。

    n的阶乘有什么好讨论的，不就是从1一直乘到n吗？没错，但如果我们换个角度来思考，将n!表示成关于n的最高次幂为n的多项式，该如何表示呢？

1!=1¹

2!=2²-2¹

3!=3³-3×3²+2×3¹

4!=4⁴-6×4³+11×4¹-6×4¹

5!=5⁵-10×5⁴+35×5³-50×5¹+24×5¹

6!=6⁶-15×6⁵+85×6⁴-255×6³+274×6²-120×6¹

……

n!=n×(n-1)×(n-2)×(n-3)×……×(n-k)×……6×5×4×3×2×1

   =n×(n-1)×(n-2)×(n-3)×……×(n-k)×……(n-n+6)×(n-n+5)×(n-n+4)×(n-n+3)×(n-n+2)×(n-n+1)

   =n×(n-1)×(n-2)×(n-3)×……×(n-k)×……[n-(n-6)]×[n-(n-5)]×[n-(n-4)]×[n-(n-3)]×[n-(n-2)]×[n-(n-1)]

   =nⁿ-{前n-1个自然数之和}×n^n-1+{前n-1个自然数两两乘积之和}×n^n-1-{前n-1个自然数三三乘积之和}×n^n-1+…+(-1)^n-1{前n-1个自然数之积}×n

   =nⁿ-S_n-1⁽¹⁾n^n-1+S_n-2⁽²⁾n^n-2+S_n-3⁽³⁾n^n-3+…+(-1)^(n-1)S_n-1^(n-1)n

    即：

    数学真是美妙，希望得到你们的共鸣！

    (注：这个公式是十年前在高中数学的学习过程中得到的，现更新至博客)