两个公式

    1.N维超立方体的M维组成个数为

    2.封闭N维空间所需要的最少N维体的各维数为

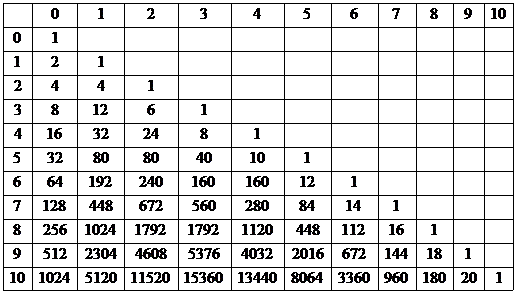
    此表列出了“N维超立方体”的“M维”组成个数。举例来说，一个立方体(3维立方体)含有8个点(0维)12条线(1维)6个面(2维)(对应上表的第三行);一个四维超立方体(虽然这很难想象)含有16个点(0维)32条线(1维)24个面(2维)和8个立方体(3维)组成(对应上表的第四行)。我曾经在纸上画过一个四维超立方体，当你动手把它画出来的时候就会发现这些数字很真实了，当然，你要有足够的想象力，因为在纸(纸是2维的)上表现3维的物体已经是我们的大脑经过处理的了，要表现4维的确很困难，更不要说5维6维了……

    无论如何，我们得到了一个计算公式，它表示了N维超立方体的M维组成个数。然后我们来解释一下第二个公式，封闭N维空间所需要的最少N维体——读起来很拗口，翻译成具体数字就没那么拗口了，二维空间，比如我们平时玩的小游戏《超级玛丽》就是一个二维世界，要在这样一个世界中封闭一个区域最少需要几条线呢?答案很明显是3条线，围成一个三角形。那么再来说我们生活的三维空间，要在三维空间中封闭一个空间至少需要几个面呢?答案是4个，围成一个三角锥。套用公式吧：封闭2维空间所需要的最少2维体(三角形)的各维数为3()个点，3()条线，1()个面;封闭3维空间所需要的最少3维体(三角锥)的各维数为4()个点，6()条线，4()个面，1()个体。

    (注：这个递推公式是十年前在高中数学的学习过程中得到的，现更新至博客)