量化存储墙以及功耗优化空间

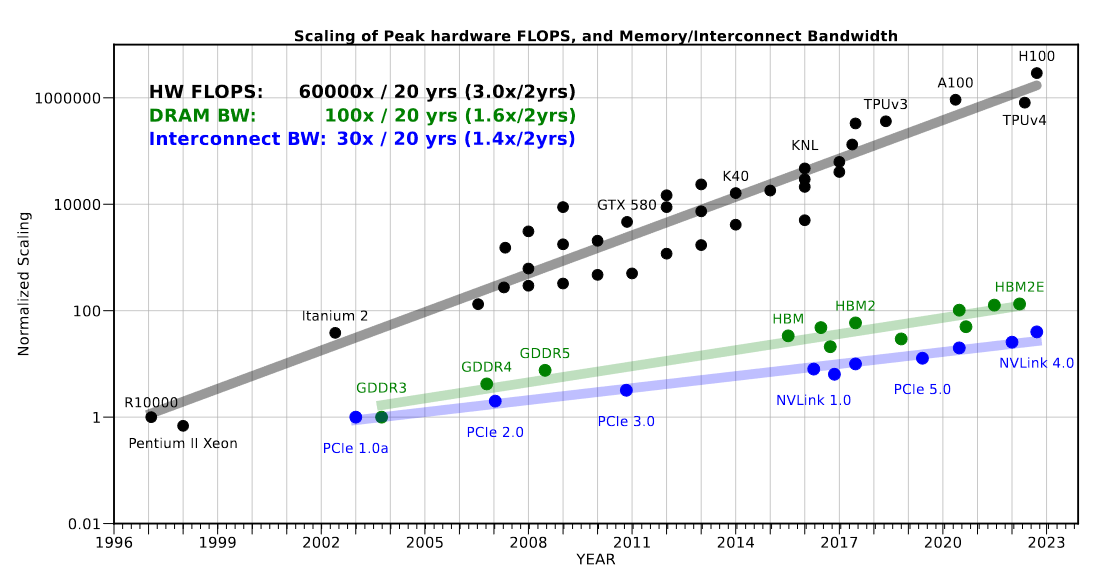
CMOS 计算和存储工艺发展步调并不一致，SOTA Memory 最高频率的远远低于 SOTA CMOS。如下图所示^[1]：

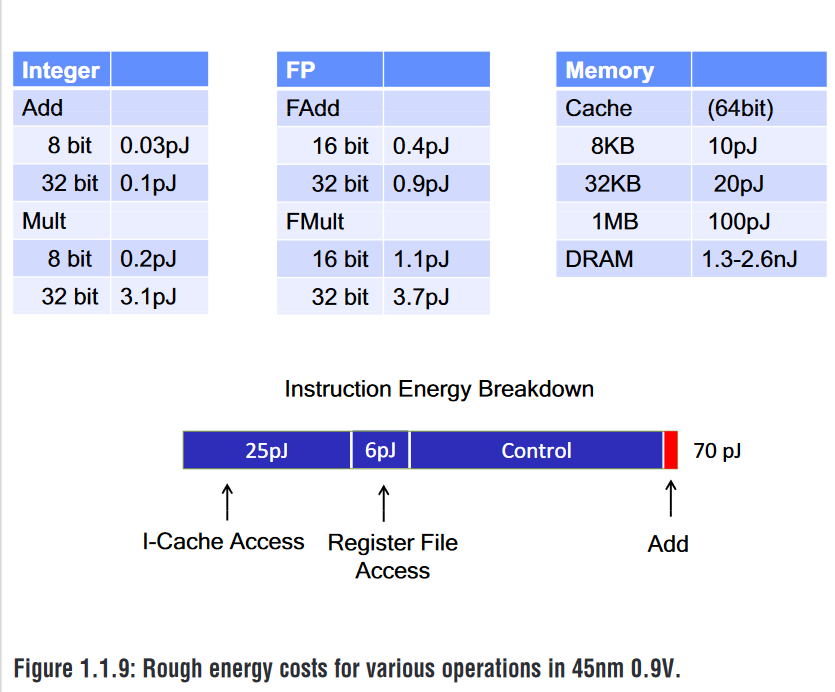
除了性能，能耗上存储也远远高于计算能耗，存储能耗受诸多譬如大小、宽度等参数影响，但不妨粗略进行数量级估计计算，如图 2014 年 ISSCC 经典的数据 45 nm 0.9V 下，计算和能耗开销^[2]

而为了尽可能发挥 CMOS 的性能，现有体系架构穿插了一层又一层的 memory hierarchy，发掘数据复用度从而发掘存储、计算系统最大 utilization。这就将算法-硬件自然地联系在一起，如 roofline model。

Roofline model 针对性能而言，本文延续 software-hardware 从能耗角度分析优化的边界所在。

compute idensity 自然地将算法和硬件、计算和存储结合在一张表上，简洁、优雅、对称，在工程领域难得有如此优雅的公式。

存储到计算的鸿沟：Gp 值

回到 ISSCC 图标，将所以计算能耗统一放缩到 64 bit 下：

Operation	Bit-width	Energy (Original)	Energy (Scaled to 64b)	Scaled Energy (Relative)
IAdd	8b	0.03pJ	0.24pJ	1.2x
IAdd	32b	0.1pJ	0.2pJ	1.0x
IMul	8b	0.2pJ	1.6pJ	8.0x
IMul	32b	3.1pJ	6.2pJ	31.0x
FAdd	16b	0.4pJ	1.6pJ	8.0x
FAdd	32b	0.9pJ	1.8pJ	9.0x
FMul	16b	1.1pJ	4.4pJ	22.0x
FMul	32b	3.7pJ	7.4pJ	37.0x
IFma	8b	0.23pJ	1.84pJ	9.2x
IFma	32b	3.2pJ	6.4pJ	32.0x
FFma	16b	1.5pJ	6.0pJ	30.0x
FFma	32b	4.6pJ	9.2pJ	46.0x

因为 AI 领域最常用的基础计算是乘加(FMA, Fused Multiply Add)，补充了乘加的能耗数据。

整数加法的门复杂度随着 bit 位数线性变化，IAdd 8b 和 IAdd 32b 放缩后能耗近似符合假设。按理 IAdd 8bit 放缩后应当比 IAdd 32bit 更加节能（8 个 8 bit Adder 对比 2 个 32bit Adder，相当于一部分 Full Adder 替换为 Half Adder ），结果相反的原因大概率是舍入误差，不影响深入分析。

将计算功耗统一 bit 位数是为了和存储对齐，存储功耗数据如下：

Memory	Size	Energy
Cache	8KB	10pJ
Cache	32KB	20pJ
Cache	1MB	100pJ
DRAM(min)	-	1.3nJ
DRAM(max)	-	2.6nJ

每次执行一次二元操作（乘法除法），读取两个操作数，输出一个操作数，要进行三次 memory access 操作，进行一次三元操作（乘加），则要进行四次 memory access 操作。

计算 \(Gp = \frac{\text{Memory Operators} \times \text{Memory Energy}}{\text{Scaled Energy}}\)，结果如下：

Memory/Operator	Iadd 8bit	Fmul 32bit	Ifma 8bit	Ffma 16bit	Ffma 32bit
Cache 8KB	125x	4.05x	21.7x	6.67x	4.35x
Cache 32KB	250x	8.11x	43.5x	13.3x	8.70x
Cache 1MB	1250x	40.5x	217x	66.7x	43.5x
DRAM min	16300x	527x	2830x	867x	565x
DRAM max	32500x	1050x	5650x	1730x	1130x

Gp 值的含义是，如果数据没有任何的复用，并且系统中只存在对应的存储和计算组件（比如只有 DRAM 和 Ffma 32bit 计算单元）时，存储能耗相比计算能耗的比例，一个非常理想的边界值，相当直观地揭示了存储能耗和计算能耗的差距(Gap)。

再计算一个 \(G = \frac{ \text{Memory Energy}}{\text{Scaled Energy}}\) ，其作用后文再提及。

Memory/Operator	Iadd 8bit	Fmul 32bit	Ifma 8bit	Ffma 16bit	Ffma 32bit
Cache 8KB	41.7x	1.35x	5.43x	1.67x	1.09x
Cache 32KB	83.3x	2.70x	10.9x	3.33x	2.17x
Cache 1MB	417x	13.5x	54.3x	16.7x	10.9x
DRAM min	5420x	176x	707x	217x	141x
DRAM max	10800x	351x	1410x	433x	283x

量化功耗优化空间

实际系统数据存在复用度，且系统中有多层memory，对于某一层的 hierarchy，不是所有的数据都会经过。为了理论分析，只考虑一层 memory 的能耗，进而对理论修正复用度。

先前计算大都以 FLOPS 的视角推导，而这次我们将从数据量的视角开始。系统的总能耗为:

\[\begin{align*} E =& E_{\text{memory}} + E_{\text{compute}}\\ =& Operands \times (e_{\text{memory}} / RU + RC \times e_{\text{compute}} / P) \end{align*} \]

• Operands ：代表数据量，比如一次乘法涉及3个操作数
• \(e_{memory}, e_{compute}\) ：对齐 bit 的存储计算能耗
• P: Pattern， operands 和 FLOPS 的桥梁，表示进行一次计算需要 operands 的数量，即前文的 Memory Operators ^[3]
• RU：Reuse，表示实际运行时的所有数据复用度的平均值（而非依赖图理论最高复用度）
• RC：Recomputation，重复运行相同计算操作的平均次数，由于底层 memory 存储有限，中间量需要复用，存在低级 memory 复用消耗存储空间进而影响其他变量的复用度，而写回去又有能耗性能损失，不如保留源操作数放弃中间变量，需要时重新计算^[4]

由于单位能耗 \(e_{memory}\) 远远大于 \(e_{compute}\)，系统中能耗一般 bottle neck 在存储能耗开销，而计算能耗对于一定的算法、一定的计算量能耗就是固定的 ^[5]，存储开销缺少硬件参数、调度策略等等决策空间极大。“优化系统能耗”基本等价于“优化存储能耗”，为了量化优化的程度，引入比值

\[O = \frac{E_{memory}}{E_{compute}} = P \times \frac{e_{memory}}{e_{compute}}\times \frac{1}{RU\times RC} = \frac{G \times P}{RU \times RC} = \frac{Gp}{RU \times RC} \]

一般来说 O > 1，这个值越小，优化结果越好。Gp 和执行计算种类以及硬件能耗表现有关，如果纯架构不涉及电路，G 一般可看作定值。可见优化的目标是使 \(RU \times RC\) 值最小。

对于一个固定算法，需要先确定基础操作，随后才能确定数据依赖图。基础操作粒度不同使得参数定义不同，比如执行乘加，如果看作先乘再加，则是 3+3=6 个操作数，而乘法器和加法器相连则是 4 个操作数，又可以将后者看作前者经过数据复用导致总访存数变化。此时不妨将 G 单独拎出来而把 \(\frac{P}{RC\times RU}\) 看作一个整体，比如根据前文数据 FFMA 16 bit，需要将 \(\frac{RC\times RU}{P}\) 拉到 200 ~ 400 ，才能使 DRAM 能耗和计算能耗相近。

功耗优化的边界：复用度的上限

优化核心就是增大 RU（数据复用度）以减轻 G 值的影响（存储计算之间的差距），对于一个固定算法，很显然 RU 存在一个最大上限，即所有数据的复用度都拉满，但 RU 受调度的顺序、硬件的 mapping 等等等影响，但终究是受制于硬件参数^[6]，硬件就一定存在一个各种工艺权衡制约导致计算和存储资源存在一个宏观边界。

采样类似 dark silicon 的做法，制定一个 benchmark ，做些实验，应该可以拟合出一个硬件参数到复用度的函数关系，然后硬件参数应该是受某个条件制约（i.e. 面积），这样可以得出硬件能耗优化的边界，即限定资源的复用度上限定律。

---

1. AI and Memory Wall ↩︎

2. Computing’s Energy Problem (and what we can do about it), ISSCC 2014 ↩︎

3. 比如前文的 3、4 ，SambaNova 中将数据模式归类为 Map、Zip、Reduce 三类，详细见 https://sambanova.ai/hubfs/23945802/SambaNova_Accelerated-Computing-with-a-Reconfigurable-Dataflow-Architecture_Whitepaper_English-1.pdf ↩︎

4. Stereo Matching Accelerator With Re-Computation Scheme and Data-Reused Pipeline for Autonomous Vehicles ↩︎

5. 除非修改算法做等价变换，类似 A = A x 5 / 5，额外增加了两次计算量，等价变换可能是可以增大 reuse 程度，进而提高整体功耗和性能，比如 FlashAttention ↩︎

6. 比如各层的 storge 非常影响复用度，例子太多了，Flash Attention，Red Blue Pupple Game 以及最近的 graph accelerator 提高底层 memory 容量 https://www.cnblogs.com/devil-sx/p/18476553 ↩︎