Analogy SRAM CIM Cell

❗️此坑还没填完

《Processing-in-Memory for AI: From Circuits to Systems》^[1]读书笔记

总的来说 Analogy SRAM Cell 的原理如下：

• SRAM 阵列中存储权重数据
• 给一个激励（表征输入数据）
• 从 SRAM 读取权重，权重和输入通过某种方式耦合输出一个信号

6T-SRAM Cell

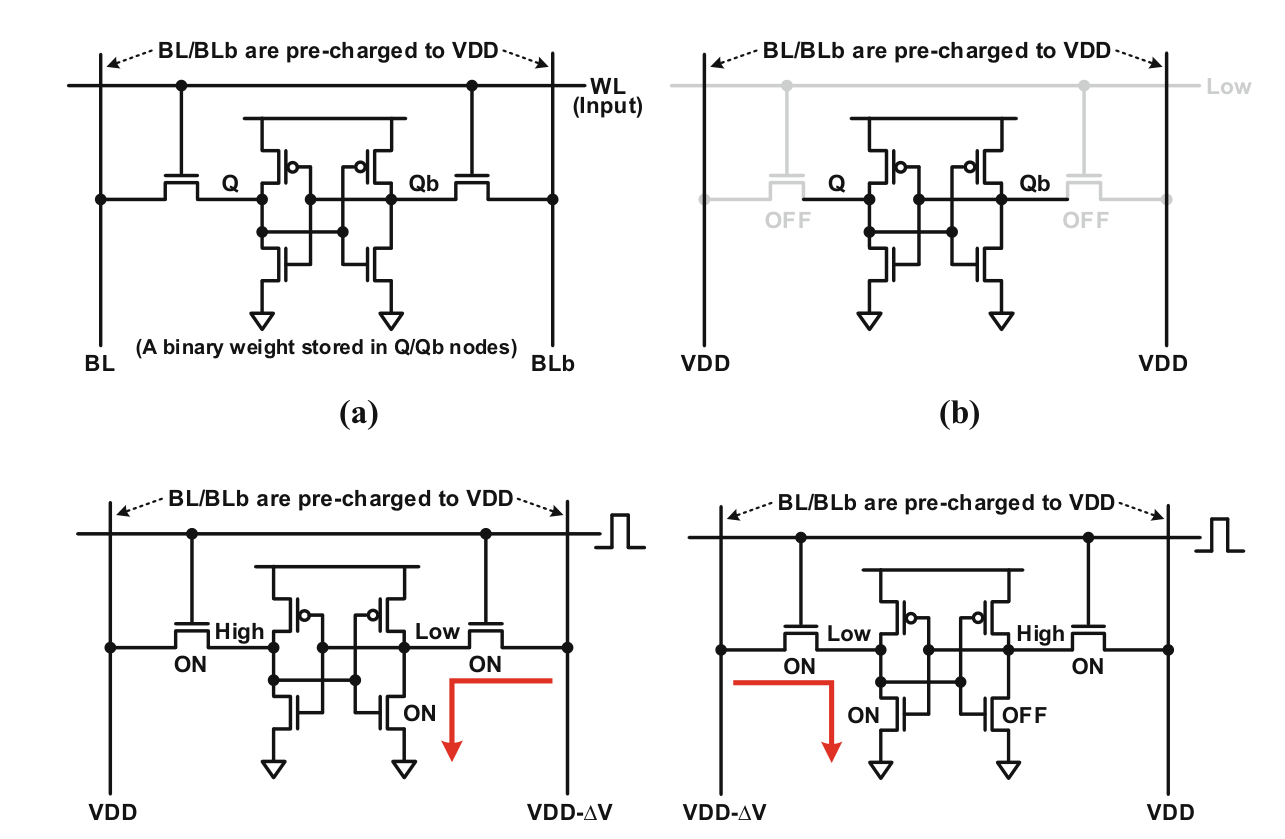
In-SRAM Operation Scheme

• Blb 和 BL Precharge 到 Vdd
• Wordline 短暂的高电平脉冲电压（或保持低电压），开启选通晶体管
• 根据存储信息不同，必有一路选通晶体管放电，Blb/BL 电压降低
• 读取降低的压差得到乘法结果

阵列则是多个 SRAM “并联”起来，多个 SRAM 共用一对 Bit Line， 由于 SRAM CIM Micro 的行和列有时不能直接反映运算上的数据结构，我把负责完成一个乘加操作的 SRAM Cell 们称作在一个求和域

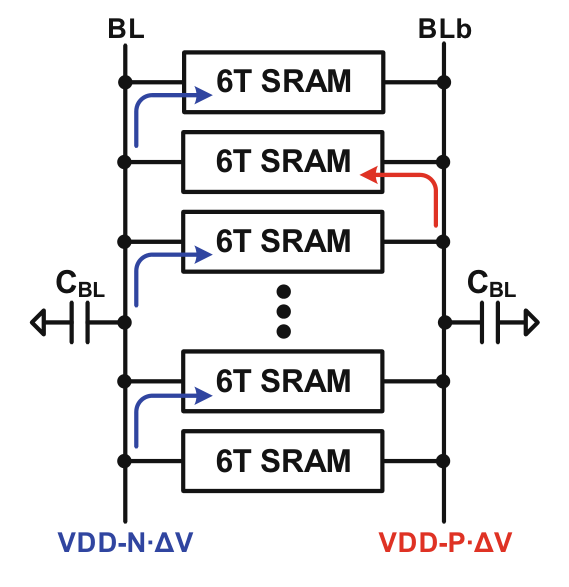
RC 回路，\(t=0\) 电容电压 \(V_0\) ， 则之后的电压函数为

\[V = V_0 e^{-\frac{t}{RC}} \]

\[\frac{\Delta V}{\Delta t} = -\frac{1}{RC} V_0 e^{-\frac{t}{RC}} \]

在 \(t=0\) 给予的脉冲时间极短，则电压变化量正比于 \(\Delta V\propto \frac{1}{RC}\) ，假设每个 SRAM 导通后的电阻相同，则并联总电导正比选通构成回路的 SRAM 数量，所以改变电压正比于选通的 SRAM (图中 P/N)，通过读取差分电压即可计算出选通数量

在 Discharge 时为保证操作线性和防止电压太低误写入 SRAM 状态，要求控制 \(\Delta V\) 极小(Dynamic Range)

这样完成了多个权重数据中的某一位和一位输入的乘加，输出一个模拟量。这样的求和域copy多个，将权重不同位的 bit 分布在不同的求和域，在后续电路中放置 ADC 和 Shifted Adder，用多个脉冲完成多位输入的乘加

即将多位权重部署在空间，将多位输入部署在时间

8T-SRAM / 10T-SRAM Cell

6T-SRAM 最大的优点是没有改变 SRAM 的结构。但这里读取和写入复用了一个接口（Bit Line），有可能误写入改变 SRAM 的状态。

简单的做法是引入额外的晶体管解耦读取和写入，读取有专用的 Read Word Line (RWL)，解耦了读取和写入，Dynamic Range 自然解决了。如下 Single Port 8T-SRAM 或 Dual Port 10T-SRAM

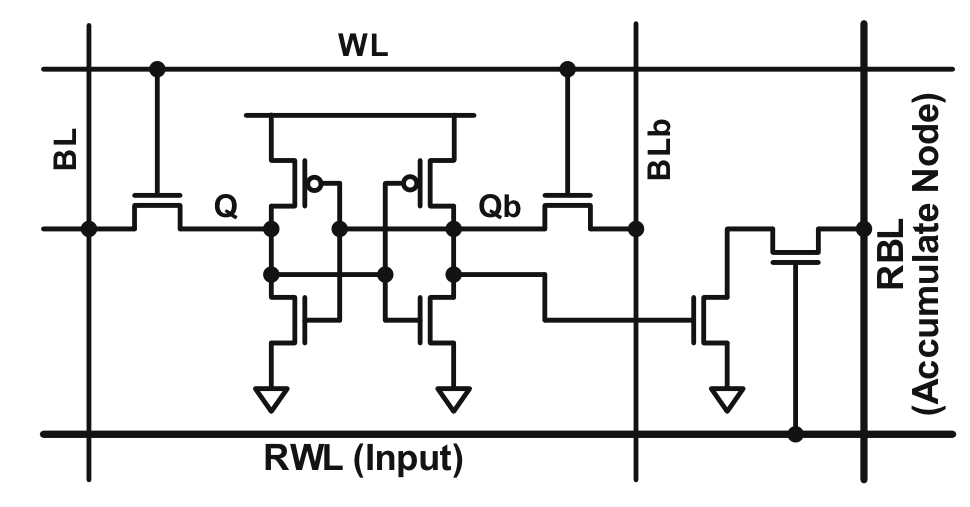
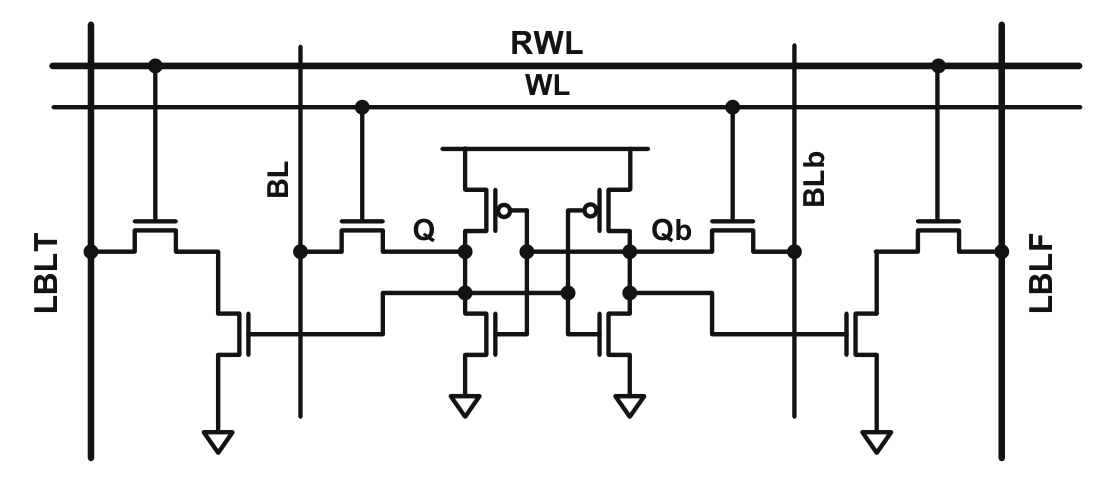
但还存在个问题没有解决：每个晶体管之间存在 device2device 的差异，即他们选通电阻 \(R_0\) 会存在方差，这就导致 \(\Delta V\) 不能很好地反映选通晶体管的数量。这本质是用电流调制电压信号带来的结果

解决思路一是引入 in-situ training 修正 device2device 之间的偏差（这种做法在忆阻器里非常常见）

解决思路二更改 Read Scheme，有没有办法直接在电压域里取平均呢？这里可以借鉴 SAR-ADC 的思路，不断更改回路拓扑结构对电压信号求平均，原本是同时激活所有求和域的 Cell，现在依次选通 Cell。缺点是会带来更加复杂的时序控制逻辑。^[2]

SAR-ADC 方案是基于电容相等的前提，难道电容之间的 device2device 偏差就相对更小吗？

不过用电流调制电压的方案很大程度受限于 Dynamic Range，正如前文 RC 放电公式，只有保证 \(\Delta V\) 非常小时才满足线性。在电压域操作扩大 Dynamic Range，就能降低其他偏差的影响

7T-SRAM

TODO。。。（后面再更吧🥱）

---

1. Processing-in-Memory for AI: From Circuits to Systems | SpringerLink. (不详). 取读于 2024年3月7日, 从 https://link.springer.com/book/10.1007/978-3-030-98781-7 ↩︎

2. Biswas, A., & Chandrakasan, A. P. (2019). CONV-SRAM: An Energy-Efficient SRAM With In-Memory Dot-Product Computation for Low-Power Convolutional Neural Networks. IEEE Journal of Solid-State Circuits, 54(1), 217–230. https://doi.org/10.1109/JSSC.2018.2880918 ↩︎