二叉查找树 操作
《算法导论》读书笔记之第12章 二叉查找树
摘要:
本章介绍了二叉查找树的概念及操作。主要内容包括二叉查找树的性质,如何在二叉查找树中查找最大值、最小值和给定的值,如何找出某一个元素的前驱和后继,如何在二叉查找树中进行插入和删除操作。在二叉查找树上执行这些基本操作的时间与树的高度成正比,一棵随机构造的二叉查找树的期望高度为O(lgn),从而基本动态集合的操作平均时间为θ(lgn)。
1、二叉查找树
二叉查找树是按照二叉树结构来组织的,因此可以用二叉链表结构表示。二叉查找树中的关键字的存储方式满足的特征是:设x为二叉查找树中的一个结点。如果y是x的左子树中的一个结点,则key[y]≤key[x]。如果y是x的右子树中的一个结点,则key[x]≤key[y]。根据二叉查找树的特征可知,采用中根遍历一棵二叉查找树,可以得到树中关键字有小到大的序列。http://www.cnblogs.com/Anker/archive/2013/01/27/2878594.html介绍了二叉树概念及其遍历。一棵二叉树查找及其中根遍历结果如下图所示:
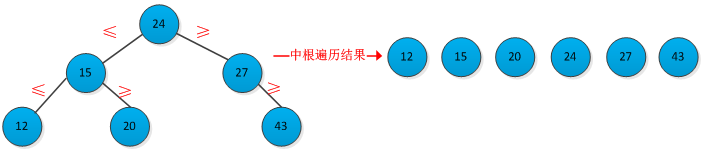
书中给出了一个定理:如果x是一棵包含n个结点的子树的根,则其中根遍历运行时间为θ(n)。
问题:二叉查找树性质与最小堆之间有什么区别?能否利用最小堆的性质在O(n)时间内,按序输出含有n个结点的树中的所有关键字?
2、查询二叉查找树
二叉查找树中最常见的操作是查找树中的某个关键字,除了基本的查询,还支持最大值、最小值、前驱和后继查询操作,书中就每种查询进行了详细的讲解。
(1)查找SEARCH
在二叉查找树中查找一个给定的关键字k的过程与二分查找很类似,根据二叉查找树在的关键字存放的特征,很容易得出查找过程:首先是关键字k与树根的关键字进行比较,如果k大比根的关键字大,则在根的右子树中查找,否则在根的左子树中查找,重复此过程,直到找到与遇到空结点为止。例如下图所示的查找关键字13的过程:(查找过程每次在左右子树中做出选择,减少一半的工作量)
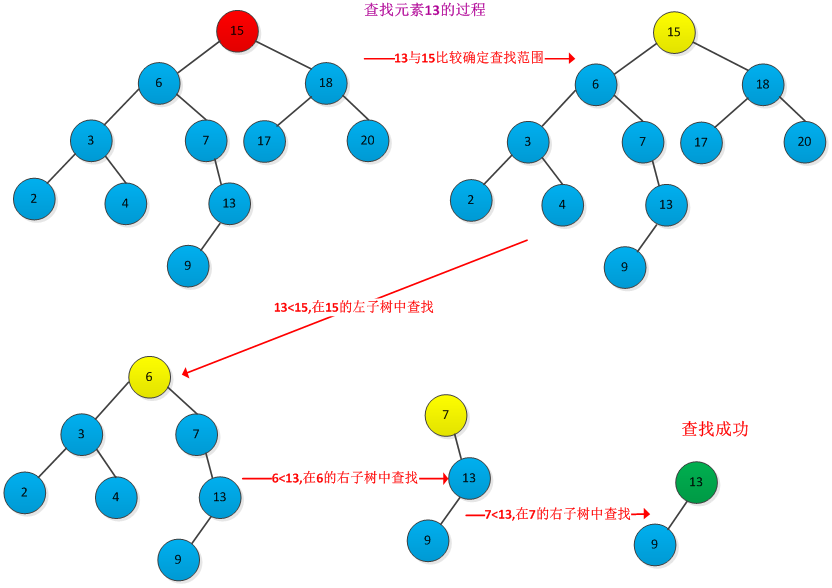
书中给出了查找过程的递归和非递归形式的伪代码:
1 TREE_SEARCH(x,k) 2 if x=NULL or k=key[x] 3 then return x 4 if(k<key[x]) 5 then return TREE_SEARCH(left[x],k) 6 else 7 then return TREE_SEARCH(right[x],k)
1 ITERATIVE_TREE_SEARCH(x,k) 2 while x!=NULL and k!=key[x] 3 do if k<key[x] 4 then x=left[x] 5 else 6 then x=right[x] 7 return x
(2)查找最大关键字和最小关键字
根据二叉查找树的特征,很容易查找出最大和最小关键字。查找二叉树中的最小关键字:从根结点开始,沿着各个节点的left指针查找下去,直到遇到NULL时结束。如果一个结点x无左子树,则以x为根的子树中,最小关键字就是key[x]。查找二叉树中的最大关键字:从根结点开始,沿着各个结点的right指针查找下去,直到遇到NULL时结束。书中给出了查找最大最小关键字的伪代码:
1 TREE_MINMUM(x) 2 while left[x] != NULL 3 do x=left[x] 4 return x
1 1 TREE_MAXMUM(x) 2 2 while right[x] != NULL 3 3 do x= right[x] 4 4 return x
(3)前驱和后继
给定一个二叉查找树中的结点,找出在中序遍历顺序下某个节点的前驱和后继。如果树中所有关键字都不相同,则某一结点x的前驱就是小于key[x]的所有关键字中最大的那个结点,后继即是大于key[x]中的所有关键字中最小的那个结点。根据二叉查找树的结构和性质,不用对关键字做任何比较,就可以找到某个结点的前驱和后继。
查找前驱步骤:先判断x是否有左子树,如果有则在left[x]中查找关键字最大的结点,即是x的前驱。如果没有左子树,则从x继续向上执行此操作,直到遇到某个结点是其父节点的右孩子结点。例如下图查找结点7的前驱结点6过程: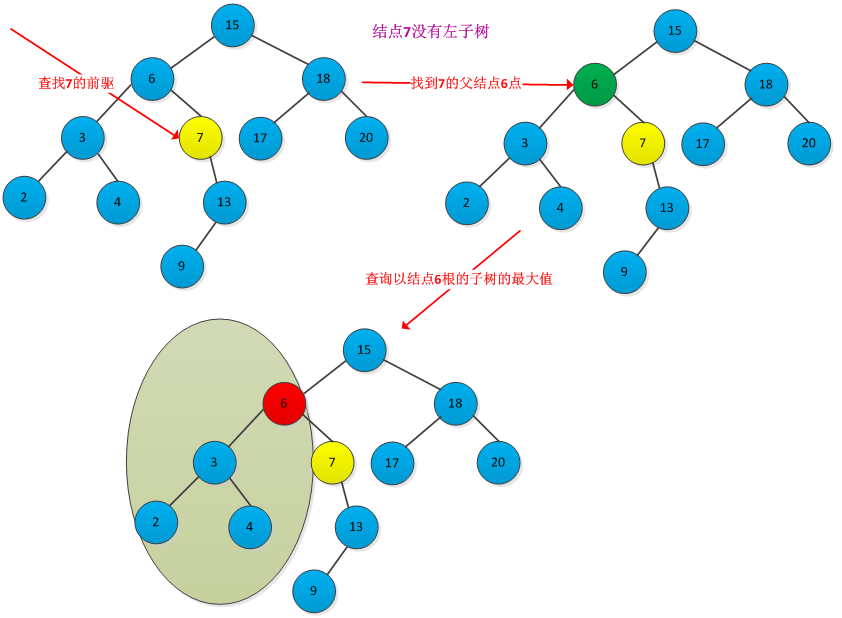
查找后继步骤:先判断x是否有右子树,如果有则在right[x]中查找关键字最小的结点,即使x的后继。如果没有右子树,则从x的父节点开始向上查找,直到遇到某个结点是其父结点的左儿子的结点时为止。例如下图查找结点13的后继结点15的过程: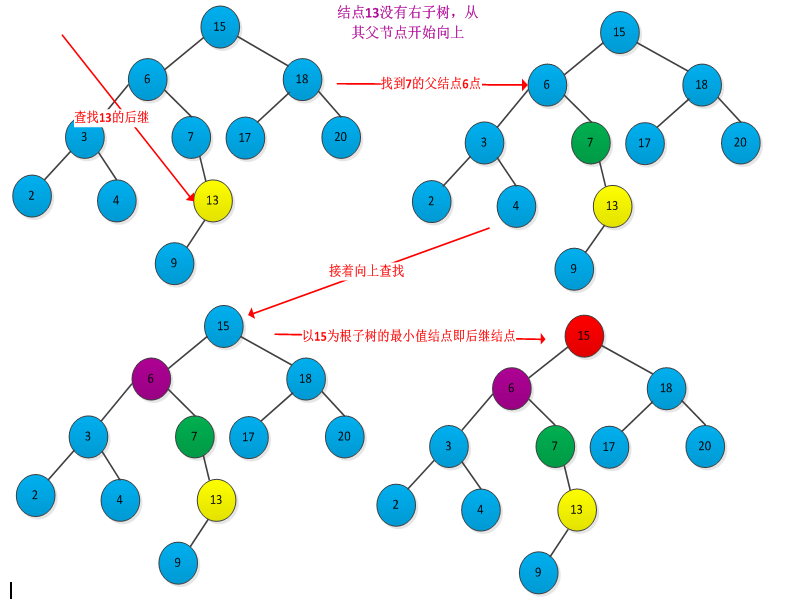
书中给出了求x结点后继结点的伪代码:
1 TREE_PROCESSOR(x) 2 if right[x] != NULL 3 then return TREE_MINMUM(right(x)) 4 y=parent[x] 5 while y!= NULL and x ==right[y] 6 do x = y 7 y=parent[y] 8 return y
定理:对一棵高度为h的二叉查找,动态集合操作SEARCH、MINMUM、MAXMUM、SUCCESSOR、PROCESSOR等的运行时间均为O(h)。
3、插入和删除
插入和删除会引起二叉查找表示的动态集合的变化,难点在在插入和删除的过程中要保持二叉查找树的性质。插入过程相当来说要简单一些,删除结点比较复杂。
(1)插入
插入结点的位置对应着查找过程中查找不成功时候的结点位置,因此需要从根结点开始查找带插入结点位置,找到位置后插入即可。下图所示插入结点过程:
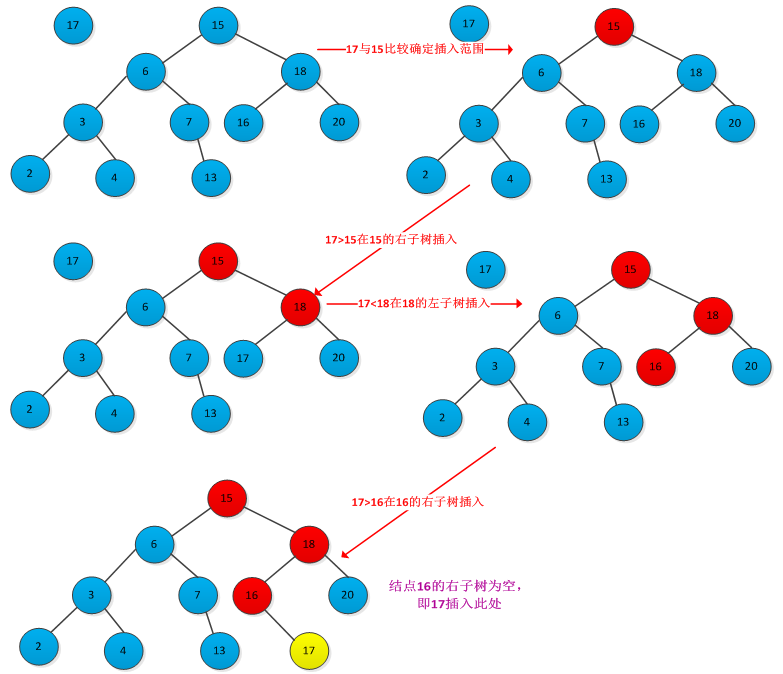
书中给出了插入过程的伪代码:
1 TREE_INSERT(T,z) 2 y = NULL; 3 x =root[T] 4 while x != NULL 5 do y =x 6 if key[z] < key[x] 7 then x=left[x] 8 else x=right[x] 9 parent[z] =y 10 if y=NULL 11 then root[T] =z 12 else if key[z]>key[y] 13 then keft[y] = z 14 else right[y] =z
插入过程运行时间为O(h),h为树的高度。
(2)删除
从二叉查找树中删除给定的结点z,分三种情况讨论:
<1>结点z没有左右子树,则修改其父节点p[z],使其为NULL。删除过程如下图所示: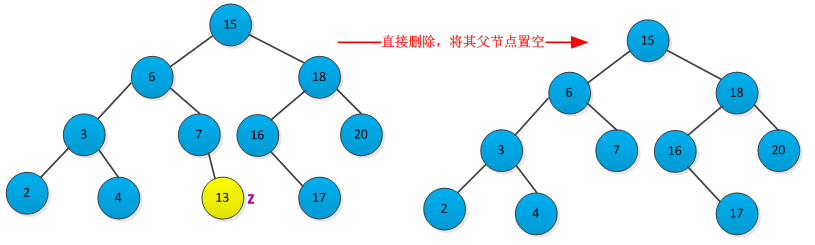
<2>如果结点z只有一个子树(左子树或者右子树),通过在其子结点与父节点建立一条链来删除z。删除过程如下图所示: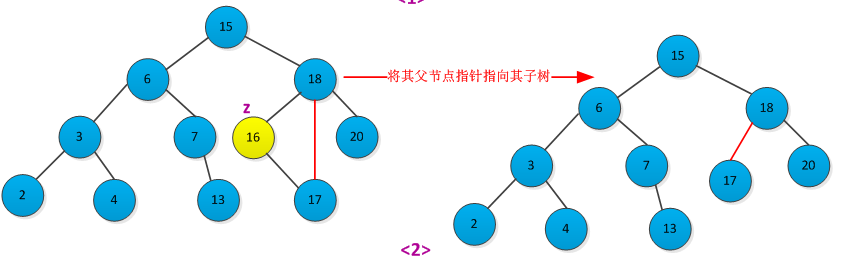
<3>如果z有两个子女,则先删除z的后继y(y没有左孩子),在用y的内容来替代z的内容。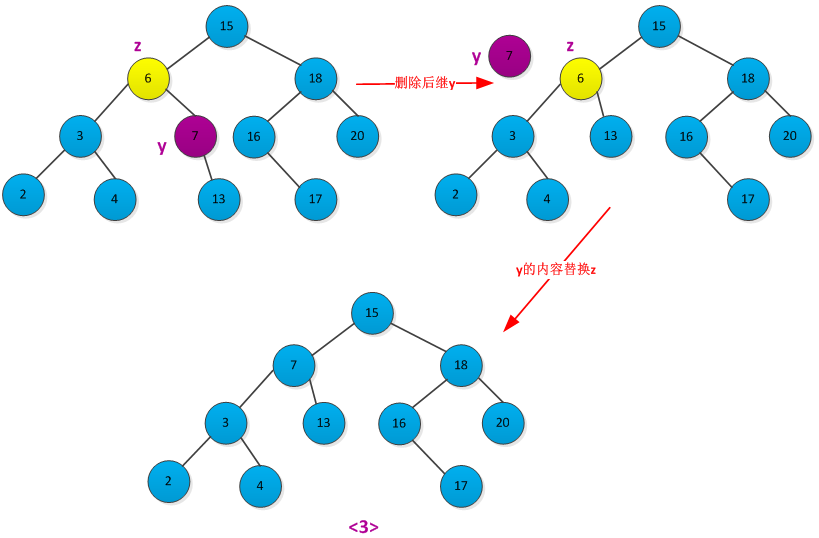
书中给出了删除过程的伪代码:
1 TREE_DELETE(T,z) 2 if left[z] ==NULL or right[z] == NULL 3 then y=z 4 else y=TREE_SUCCESSOR(z) 5 if left[y] != NULL 6 then x=left[y] 7 else x=right[y] 8 if x!= NULL 9 then parent[x] = parent[y] 10 if p[y] ==NULL 11 then root[T] =x 12 else if y = left[[prarnt[y]] 13 then left[parent[y]] = x 14 else right[parent[y]] =x 15 if y!=z 16 then key[z] = key[y] 17 copy y's data into z 18 return y
定理:对高度为h的二叉查找树,动态集合操作INSERT和DELETE的运行时间为O(h)。
4、实现测试
采用C++语言实现一个简单的二叉查找树,支持动态集合的基本操作:search、minmum、maxmum、predecessor、successor、insert和delete。设计的二叉查找树结构如下所示:
1 template <class T>
2 class BinarySearchTreeNode
3 {
4 public:
5 T elem;
6 struct BinarySearchTreeNode<T> *parent;
7 struct BinarySearchTreeNode<T>* left;
8 struct BinarySearchTreeNode<T>* right;
9 };
10
11 template <class T>
12 class BinarySearchTree
13 {
14 public:
15 BinarySearchTree();
16 void tree_insert(const T& elem);
17 int tree_remove(const T& elem );
18 BinarySearchTreeNode<T>* tree_search(const T& elem)const;
19 T tree_minmum(BinarySearchTreeNode<T>* root)const;
20 T tree_maxmum(BinarySearchTreeNode<T>* root)const;
21 T tree_successor(const T& elem) const;
22 T tree_predecessor(const T& elem)const;
23 int empty() const;
24 void inorder_tree_walk()const;
25 BinarySearchTreeNode<T>* get_root()const {return root;}
26 private:
27 BinarySearchTreeNode<T>* root;
28 };
完整程序如下所示:
 View Code
View Code程序测试结果如下所示:
二叉树实现时候添加了一个父结点指针,方便寻找给定结点的前驱和后继。二叉树中删除操作实现比较复杂,需要分类讨论,我分三种情况进行讨论,程序写的有些繁琐,可以进行优化。优化后的代码如下:
1 template <class T>
2 int BinarySearchTree<T>::tree_delete(const T& elem)
3 {
4 //找到该元素对应的结点
5 BinarySearchTreeNode<T>* pnode = tree_search(elem);
6 if(NULL != pnode)
7 {
8 BinarySearchTreeNode<T> *qnode,*tnode;
9 //判断结点是否有左右孩子
10 if(pnode->left == NULL || pnode->right == NULL)
11 qnode = pnode; //有一个左孩子或者一个右孩子和没有左右孩子
12 else
13 qnode = tree_search(tree_successor(elem)); //有左右孩子
14 if(NULL != qnode->left)
15 tnode = qnode->left;
16 else
17 tnode = qnode->right;
18 if(NULL != tnode)
19 tnode->parent = qnode->parent;
20 if(qnode->parent == NULL)
21 root = tnode;
22 else
23 if(qnode == qnode->parent->left)
24 qnode->parent->left = tnode;
25 else
26 qnode->parent->right = tnode;
27 if(qnode != pnode)
28 pnode->elem = qnode->elem; //将后继结点的值复制到要删除的结点的值
29 delete qnode;
30 return 0;
31 }
32 return -1;
33 }
5、随机构造二叉查找树
二叉查找上各种基本操作的运行时间都是O(h),h为树的高度。但是在元素插入和删除过程中,树的高度会发生改变。如果n个元素按照严格增长的顺序插入,那个构造出的二叉查找树的高度为n-1。例如按照先后顺序插入7、15、18、20、34、46、59元素构造二叉查找树,二叉查找树结构如下所示: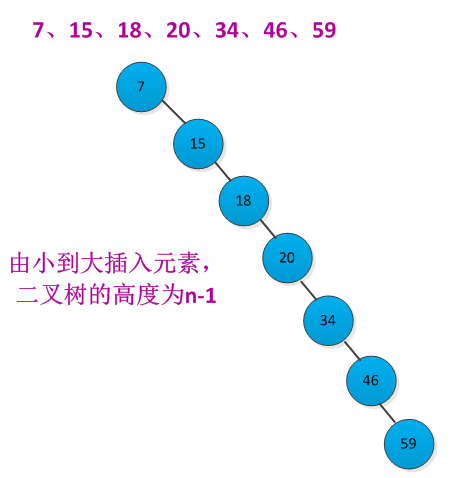



 浙公网安备 33010602011771号
浙公网安备 33010602011771号