散列表
注：本随笔没有代码实现，仅是对散列表这一数据结构进行讲解，涵盖了散列表中常用的全部思想，参考《算法导论》。具体数学证明，还得自己查看《算法导论》哈，嘻嘻。
直接寻址表：一个可以存储全部关键字的“大小合理”的数组。（当全部关键字数目巨大时，此时数组要想装下全部关键字，其大小就是不合理的，会消耗大量物理空间，甚至物理空间的大小都不够）。
散列表：使用一个长度与实际存储的关键字数目成比例的数组来存储。
由于散列表是按比例设置数组大小的，所以计算数组下标时就要采用一个函数，称为“散列函数”。
由于实际存储的关键字的数目大于“散列表”的大小，那么通过“散列函数”计算后的数组下标一定会用相同的，即至少会有俩个元素存放在同一个位置，我们称之为“冲突”。
因此设计散列表主要考虑两个因素：散列函数的设计，以及如何解决冲突。
装载因子：给定一个能存放N个元素的，具有M个槽位的散列表T，则T的装载因子为 N/M;他可以小于，等于或大于1。
简单均匀散列：假定任何一个给定元素等可能地散列到M个槽位中的任何一个，且与其他元素被散列到什么位置上无关。
一个好的散列函数，应近似的满足“简单均匀散列”假设。
一、设计散列函数：
散列函数：1.启发式方法（用除法进行散列和用乘法进行散列）
2.全域散列（利用随机技术）
启发式方法：
将关键字转换为自然数：利用ASCII 字符集，如P=112，T=116.
1.除法散列法（选择M比较重要）：通过取 “K除以M的余数”，将余数作为数组下标，将关键字K映射到有M个槽位的散列表T中。
例：关键字为100，散列表大小为12.则其数组小标为4 （100=12*8+4）；
其中散列表的初始大小M的选择也会很有玄学，要尽量避免选择 m=2p, 如果关键字K是按2P表示的话，那么冲突的几率可想而知，火星撞地球。
所以一个不太接近2的整数幂的素数，是一个比较好的选择。
2.乘法散列法：
第一步：用关键字K乘以常数A（0<A<1）, 并提取KA的小数部分。
第二步：用M乘以这个值，并向下取整。
全域散列：
全域散列的思想是，在执行开始时，就从一组精心设计的函数中，随机地选择一个作为散列函数。因为是随机的选择散列函数，算法在每一次执行时都会哦有所不同们甚至对于相同的输入都会如此。
二、解决冲突：
1.链接法：其思想是将在数组同一个槽中的碰撞元素存放在一个链表中。
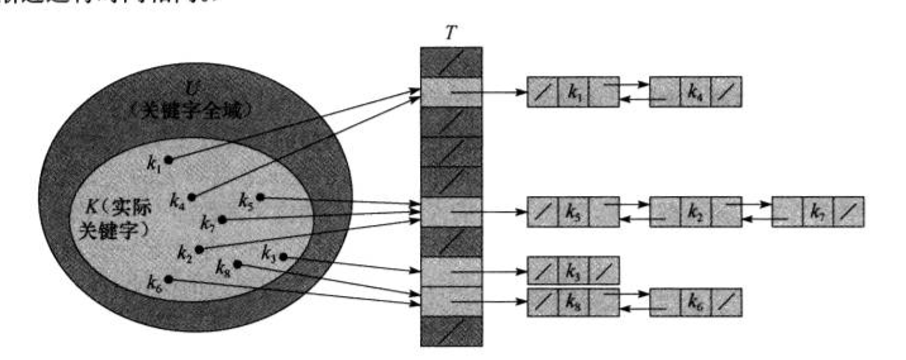
2.开放寻址法：在开放寻址法中，所有元素都放在散列表中。不像链接法，这里没有链表。
在开放寻址法中，散列表可能会被填满，以至于不能插入新元素，该方法导致的一个结果便是装载因子绝不能超过1。
在开放寻址法中插入一个元素，需要连续的检查散列表，称之为探查。
线性探查：给定关键字K,先探查通过散列函数H计算出的H(k),若被占用则探查H(K)+1，直到数组下界。
线性探查随着连续被占用的槽不断增加，平均查找时间也随之不断增加。这称为一次群集。
二次探查：给定关键字K，先探查通过散列函数H计算出的H(k)，若被占用则增加偏移，H(K)+C1*i +C2*i²，称为偏移量。
相较于“线性探查”，二次探查效果相对较好，但同样随着探查槽位不断被占用，平均查找时间也随之不断增加。这称为二次群集。
双重散列：给定关键字K，先探查通过散列函数H计算出的H(k)，若被占用则增加偏移，使用辅助散列函数H1(K)+H(K)。
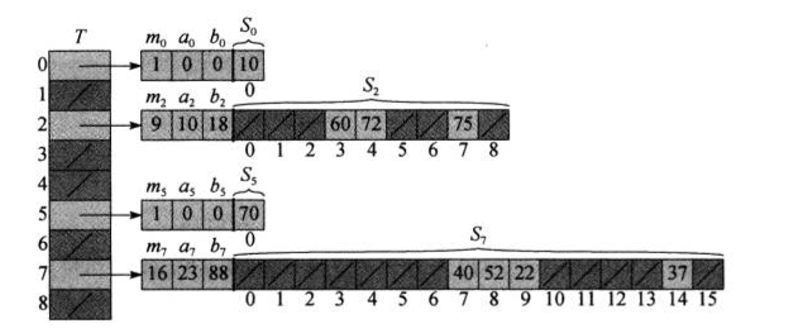
三、完全散列：
实现是将关键字通过散列函数H(K)计算出数组下表后，数组中再存放一个散列表。即H(75)=2，则75存在下标2的数组位置上，下标为2的位置还是一个散列表，H1(75)=7，则最终75存放在，下标为2的数组位置的散列表中，再此散列表中，存放在位置7处。
