对几种常见贷款进行数据分析
最近在看《Python编程导论》(第二版), 看到类那一章时,后面有个对比几种不同类型贷款的例子,有一天在回看时,突然发现,这不就是一种量化的方式么?之前本来是草草地一带而过,现在又来了兴趣,打算仔细研究研究。
注:本文对书中原有的代码基本不做改动,主要通过注释的方式进行说明,并增加了另一种贷款方式进行比较,旨在帮助大家对代码做进一步分析。
一、什么是是量化?
“量化”从字面上可以理解为数量化,如果应用在投资领域上的话,简单的说,就是将每一种投资产品,通过数据分析的方式,将其特点(风险、潜力等等)用详细的数据反映出来,更好地指导投资者获取稳定收益。
其实现在很多金融产品都是非常复杂的,普通投资者没点金融常识根本看不懂。不会计算产品的实际收益,看不到潜在的风险,很容易就被套住了。所以,如果有量化分析的经验,就可以对产品有比较清楚的了解。
好了,先来看看书中描述几种贷款方式吧:
1.每月偿还固定金额的贷款(简称等额本息贷款);
2.先还一笔固定点数(百分比)的贷款,然后每月再以较低的利率还款(简称固定点数贷款);
3.先以较低的利率还款,满x个月后再以较高的利率还款(简称双利率贷款)。
二、简述各种贷款类型
1.等额本息贷款
在查等额本息的概念时,发现还有一种叫做等额本金的贷款方式也会被经常用到,下面将依次做介绍。
等额本息:根据固定的还款时间,计算出应还的总利息,再加上本金,然后每个月平均等额的还款。
根据贷款总额loan、月利率r及还款时间m(月),可以推导出每个月的还款金额。
假设每月固定还款X,则每月的还款情况如下:
月数 | 每月剩余欠款
0 | loan
1 | loan*(1 + r) - X
2 | [loan*(1 + r) - X] * (1 + r) - X => loan*(1+r)^2 - X*(1+r) -X
3 | [loan*(1+r)^2 - X*(1+r) -X]*(1+r) - X => loan*(1+r)^3 - X*(1+r)^2 -X*(1+r) -X
... ...
n | loan*(1+r)^n - X*(1+r)^(n-1) -X*(1+r)^(n-2) - ... -X(1+r)^0
当n=m时,欠款为0,即:
loan*(1+r)^m - X*(1+r)^(m-1) - X*(1+r)^(m-2) - ... - X(1+r)^0 = 0
观察等号左边,不看第一项,提取其余多项式的-X公约数后,发现其实是一个首项a1为1, q=1+r,项数为m的等比数列,根据等比数列的求和公式Sn = a1*(1 - q^n)/(1 - q) 得:
loan*(1+r)^n - X[(1+r)^0 + (1+r)^1 + ... + (1+r)^(m-1)] = 0
loan*(1+r)^n -X*(1-(1+r)^m) / (-r) = 0
即:
loan*(1+r)^n = X*[(1+r)^m-1]/r
所以得到:
X = loan*r*(1+r)^n/[(1+r)^m-1]
那么针对等额本息的还款方式,我们就可以用Python写一个专门的函数,这样就不用每次计算的时候都把这个公式推导一遍了:
def findPayment(loan, r, m):
# 计算在贷款额loan 月利率r和期限m个月下,每月需返还的固定金额
return loan * ((r * (1 + r) ** m) / ((1 + r) ** m - 1))
这样,每次在计算等额本息贷款的每月还款金额时,只需要将贷款总额loan, 月利率r和还款总月数m代入此函数中,就能得出结果了。
2.等额本金贷款
等额本金相对来说要简单一些,每月所还的本金是相同的,利息由每个月的剩余本金计算得出。
第n个月需还的金额:(loan/m) + (loan - n * loan/m) * r
3.固定点数贷款
按照定义,我们在首次还款时先按固定的点数还一部分贷款,然后再按较低的利率还完剩余的贷款。
4.双利率贷款
前x个月以较低的r1利率还款,后m-x个月以较高的r2利率还款(假设还款总月数为m)。
三、编写与贷款相关的类及子类
我们研究的贷款类型一共有4种(书中的3种+等额本金贷款),所以最好的办法是先定义一个贷款大类,里面包含贷款的基本属性,然后根据各种类型贷款的不同,再定义不同的子类。具体过程如下:
class Mortgage(object):
# 构建贷款类, 定义四种贷款都有的属性
def __init__(self, loan, annRate, months):
self.loan = loan # 贷款总额
self.rate = annRate / 12 # 将年利率转化为月利率
self.months = months # 还款月数
self.paid = [0.0] # 已支付金额
self.outstanding = [loan] # 剩余本金
self.payment = findPayment(loan, self.rate, months) # 每月还款金额, 默认按照等额本息的方式
self.legend = None # 贷款描述
def makePayment(self):
# 还款函数,调用此函数进行还款
self.paid.append(self.payment)
reduction = self.payment - self.outstanding[-1] * self.rate # 还款金额中的本金
self.outstanding.append(self.outstanding[-1] - reduction) # 记录剩余本金
def getTotalPaid(self):
# 返回已支付贷款总额
return sum(self.paid)
def __str__(self):
# 返回贷款描述
return self.legend
class Fixed(Mortgage):
# 等额本息子类
# 只需继承Mortgage(),重写描述属性self.legend即可
def __init__(self, loan, r, months):
Mortgage.__init__(self, loan, r, months)
self.legend = "等额本息, " + str(round(r * 100, 2)) + '%'
def totalCapitalPayment(loan, months, r):
# 等额本金类贷款每个月要还的本金不变,而利息是随着还款月数的增加而减少的,所以定义一个函数,直接返回一个包含每月还款金额的列表即可
total = []
for m in range(months):
total.append(loan / months + (loan - m * (loan / months)) * r)
return total
class FixedCapital(Mortgage):
# 等额本金子类
def __init__(self, loan, r, months):
Mortgage.__init__(self, loan, r, months)
# self.payment =capitalPayment(loan, r, months)
self.capital = loan / months
self.total = totalCapitalPayment(loan, months, self.rate)
self.legend = "等额本金, " + str(round(r * 100, 2)) + '%'
def makePayment(self, m):
# 由于等额本金的每月还款额与当前还款月数相关,所以引入还款月数m
self.paid.append(self.total[m])
# 本期剩余本金 = 上期剩余本金 - 每月固定本金
self.outstanding.append(self.outstanding[-1] - self.capital)
class FixedWithPts(Mortgage):
# 固定点数子类
def __init__(self, loan, r, months, pts):
Mortgage.__init__(self, loan, r, months)
self.pts = pts # 固定点数
# 计算第一次按照固定点数还款的金额
self.paid = [self.loan * (self.pts / 100)]
self.legend = "固定点数, " + str(round(r * 100, 2)) + '%, ' + str(pts) + ' points'
class TwoRate(Mortgage):
# 双利率子类
def __init__(self, loan, r, months, teaserRate, teaserMonths):
Mortgage.__init__(self, loan, teaserRate, months)
self.teaserMonths = teaserMonths # 前期低利率月数
self.teaserRate = teaserRate # 前期低利率
self.nextRate = r / 12 # 后期高利率
self.legend = '双利率, ' + str(teaserRate * 100) + '% for ' + str(self.teaserMonths) + ' months, then ' + \
str(round(r * 100, 2)) + '%'
def makePayment(self):
# 如果到达teaserMonths,则使用self.nextRate高利率,后面每月的付款金额按照剩余本金、利率和月数重新计算
if len(self.paid) - 1 == self.teaserMonths:
self.rate = self.nextRate
self.payment = findPayment(self.outstanding[-1], self.rate, self.months - self.teaserMonths)
Mortgage.makePayment(self) # 未到达teaserMonths时,每月的还款金额
然后再定义一个比较各类贷款的函数,打印出各自的总还款额:
def compareMortgages(amt, years, fixedRate, pts, ptsRate, lowRate, highRate, lowMonths):
# 比较各类贷款的总还款额
totMonths = years * 12
fixed1 = Fixed(amt, fixedRate, totMonths)
fixed2 = FixedCapital(amt, fixedRate, totMonths)
fixed3 = FixedWithPts(amt, ptsRate, totMonths, pts)
twoRate = TwoRate(amt, highRate, totMonths, lowRate, lowMonths)
morts = [fixed1, fixed3, twoRate] # 先对除等额本金外的其他三类贷款进行还款
for m in range(totMonths):
for mort in morts:
mort.makePayment()
fixed2.makePayment(m) # 单独调用包含参数m的等额本金还款参数
morts.insert(1, fixed2) # 还款完毕后再加入贷款列表
# 展示四种贷款方式各自的还款总额
for m in morts:
print(m)
print(" Total payments = $" + str(int(m.getTotalPaid())))
# 带入实际的值进行比较:
compareMortgages(200000, 30, 0.07, 3.25, 0.05, 0.045, 0.095, 48)
# 比较结果
Fixed, 7.0%
Total payments = $479017
Fixed Capital, 7.0%
Total payments = $410583
Fixed, 5.0%, 3.25 points
Total payments = $393011
4.5% for 48 months, then 9.5%
Total payments = $551444
从比较结果可以看出,还款总额从高到低依次为:
双利率 > 等额本息 > 等额本金 > 固定点数
四、使用pylab定义绘制还款曲线函数
只看还款总额还分析地不够彻底,可以通过绘制曲线的方式直观地比较这几种贷款,哪个最划算(或者哪个最坑),所以可以按照每月还款额、还款总额、剩余本金、支付的总利息这几个维度进行分析。
在Mortgage()类中分别添加统计这些信息的函数:
def plotPayments(self, style):
# 统计每月还款额
pylab.plot(self.paid[1:], style, label=self.legend)
def plotTotPd(self, style):
# 统计每月还款总额
totPd = [self.paid[0]]
for i in range(len(self.paid)):
totPd.append(totPd[-1] + self.paid[i])
pylab.plot(totPd, style, label=self.legend)
def plotBalance(self, style):
# 统计每月剩余本金
pylab.plot(self.outstanding, style, label=self.legend)
def plotNet(self, style):
# 统计每月支付总利息
totPd = [self.paid[0]]
for i in range(1, len(self.paid)):
totPd.append(totPd[-1] + self.paid[i])
# 先通过数组计算出每月偿还的本金(贷款总额 - 每月剩余本金)
equityAcquired = pylab.array([self.loan] * len(self.outstanding)) - pylab.array(self.outstanding)
# 再用每月的总还款额 - 每月偿还本金 = 每月偿还利息
net = pylab.array(totPd) - equityAcquired
pylab.plot(net, style, label=self.legend)
为了能够绘制出这些曲线,我们还需要定义一个绘图函数,并且设置标题、标签等属性,让每个图都更加美观:
def plotMortgages(morts, amt):
def labelPlot(figure, title, xLabel, yLabel):
pylab.figure(figure) # 指定当前图,即绘制前要先指定图的figure值
pylab.title(title) # 设置标题
pylab.xlabel(xLabel) # 设置x轴标签
pylab.ylabel(yLabel) # 设置y轴标签
pylab.legend(loc='best') # 将描述信息放在不与曲线冲突的最合适区域
styles = ['k-', 'k-.', 'k:', 'b-'] # 设置各类贷款对应的曲线样式
payments, cost, balance, netCost = 0, 1, 2, 3 # 设置图的figure,对各类曲线按照指标分类
for i in range(len(morts)):
pylab.figure(payments) # 根据figure值,将各类曲线绘制到对应的图中
morts[i].plotPayments(styles[i]) # 月还款额
pylab.figure(cost)
morts[i].plotTotPd(styles[i]) # 总还款额
pylab.figure(balance)
morts[i].plotBalance(styles[i]) # 剩余本金
pylab.figure(netCost)
morts[i].plotNet(styles[i]) # 月支付利息
labelPlot(payments, '贷款' + str(amt) + '元的每月还款情况', '月数', '月还款金额')
labelPlot(cost, '贷款' + str(amt) + '元的还款总额', '月数', '已支付金额')
labelPlot(balance, '贷款' + str(amt) + '元的每月本金剩余情况', '月数', '剩余未还本金')
labelPlot(netCost, '贷款' + str(amt) + '元的累计利息支付情况', '月数', '支付的累计利息')
最后在比较函数compareMortgages()函数中进行调用即可:
def compareMortgages(amt, years, fixedRate, pts, ptsRate, lowRate, highRate, lowMonths):
# 比较各类贷款的总还款额
totMonths = years * 12
""" ... 此处省略前面的部分代码 ... """
# for m in morts:
# print(m)
# print(" Total payments = $" + str(int(m.getTotalPaid())))
# 展示四种贷款方式的对比曲线
plotMortgages(morts, amt)
pylab.show()
注: 第一次运行时,图像上的中文可能会不显示,这是因为默认字体不是中文,在代码开头导入matplotlib包并做相关设置即可:
import matplotlib
# 修改默认字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.family'] = 'sans-serif'
五、分析各类曲线
最后我们得到了4张反应贷款各个指标的分析图:
1.每月还款额的变化:

可以看出,等额本息和固定点数从始至终都维持着恒定的还款金额,但是由于固定点数提前还了一部分的贷款,所以后期支付的金额就会少一些;
等额本金是唯一一个利率呈负增长的贷款,因为每月的还款额与剩余本金息息相关,所以一开始支付的金额是最高的,但利息会随着本金的不断减少,到了最后一个月,甚至只还了558块多。适合贷款前期有充裕的钱进行还款的人群;
双利率虽然前48个月的还款额最低,但是后面的300多个月,都不得不付给银行高额的贷款。
2.整个贷款周期的本金+利息总和:
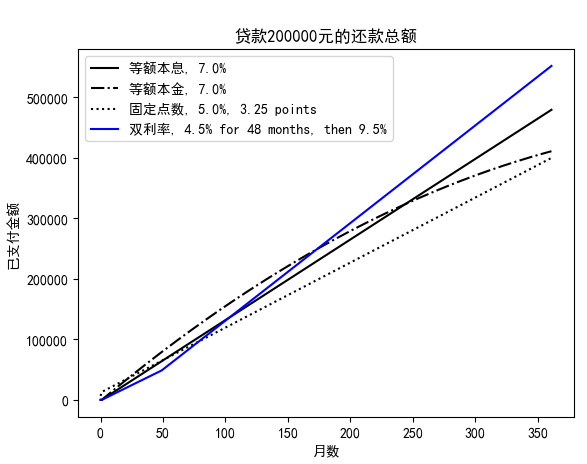
该图反映了总还款额随时间变化的情况。如果对比最后贷款结束时的还款金额,很明显,固定点数 < 等额本金 < 等额本息 < 双利率。
而在整个还款过程中,总还款额的增长速率也并非一直不变。例如,除了等额本息和固定点数外(每月还款数固定),等额本金的增长幅度是先快后慢(曲线是一段弧线);而双利率的模式则是先慢后快,有一个明显的拐点。用前期很少的还款额做诱饵,引诱借款人最终偿还高达551444元的高额贷款(别紧张,你没有看错,200000元的本金+351444元的利息)。
3.剩余未还本金的情况:
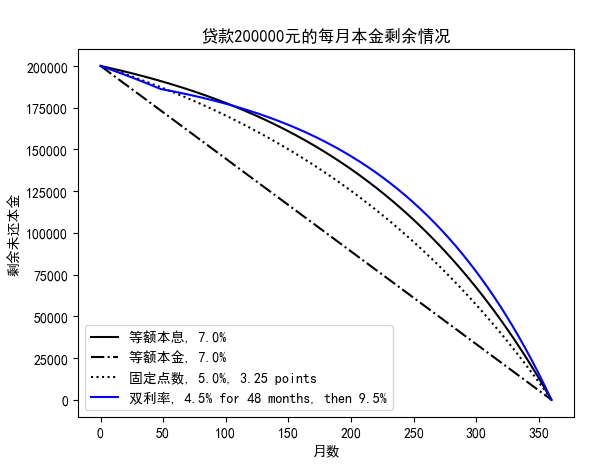
因为4类贷款的本金都是200000万,所以起点是相同的。曲线越陡峭,则说明,本金的还款速度越快;曲线越平滑,就说明可能每个月给银行还的钱大部分都用来付利息了。
4.每月累计支付的利息情况:
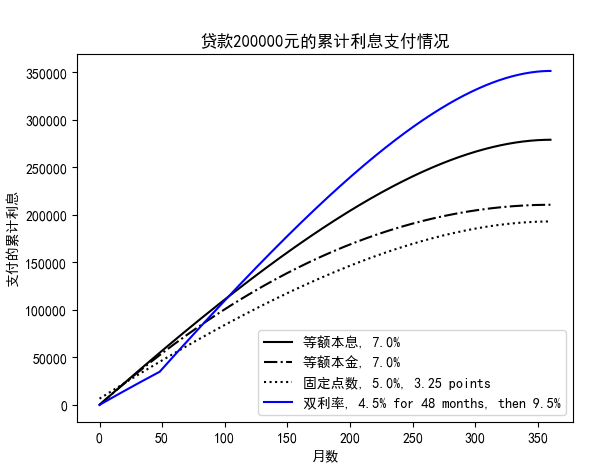
大体上都呈抛物线,可以看到,即使最划算的固定点数模式的贷款,在经历了30年后,也不得不支付高达193011元的利息,基本上已经跟本金差不多了。所以,这就是银行用复利在赚很多借款人的钱。而大部分人可能还觉得,这样的还款方式好像还OK,但是如果经过了这样量化分析后,感觉还是挺吓人的,所以没事还是少贷款吧。
六、结语
通过这样一步步的分析,我们在了解了这些贷款的各种信息后,同时也提高了自己的编码能力和数据分析的能力,简直是一举三得~这本书中还有一些其他很有意思的问题,涉及面很广,有兴趣的同学可以做深入研究。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号