算法入门 - 递归的原理及应用

递归是一种比较绕的算法，这是因为它通常在我们肉眼所见的范围内无法完成调用。迄今为止，我们学习的数组、链表等，实现的代码都是从上至下依次执行的，即便会有循环，但也是在可控范围内进行的操作。而递归却有一种无法掌控的感觉，跑着跑着就不知道去哪了。初学这种算法的同学，经常会陷入一层层的调用中，搞得头脑发晕，时而明白，时而糊涂，真的是让人头疼！🤣
实际上，是我们把递归想得过于复杂了，从本质上来说，它就是函数调用，只不过调用的是它自己。

1.从分而治之的角度看递归

递归实际上是一种分而治之的思想，一个问题，如果一下子搞不定，能否只搞定一部分呢？如此进行拆解下去，便将一个复杂的问题分解成了多个较为简单的问题，直到碰到一个问题是显而易见可解决的。我们再拿这个解决了的问题，去求解它上一层的问题，再这么反向求解下去，就可以得到最初问题的解了！

下面我们以计算阶乘为例，来详细看一下递归的过程。
我们都知道，一个数的阶乘就是从这个数开始做乘法，每次减一后继续乘，直到这个数为1（1！）。假设要求10的阶乘，就是10*9*8*7*6*5*4*3*2*1。如果用递归的思维来看，我们一下子无法求出10!，但我们知道，10! = 10 * 9!，所以问题就拆解为求9!，9!也无法直接求出，所以再拆解为 9 * 8!，一直这么拆解下去，直到 2! = 2 * 1!，此时我们知道，1! = 1，这就是我们显而易见可解决的问题，再这么反向求解过去，就可以得到最终的结果。

public class FactNum{
    public static int factorial(int n){
        // 如果n为1，就直接返回1
        if (n == 1) return 1;
        // 否则就简化为求n-1的阶乘
        return n * factorial(n-1);
    }

    public static void main(String[] args) {
        int result = factorial(5);
        System.out.println("5的阶乘为: " + result);
    }
}
/*
输出结果：
5的阶乘为: 120
*/

代码很简短，只是重复做了两件事：
1.每次都看一下当前的数 n 是不是1，如果是1，就直接返回1；
2.否则就返回 n 乘以 n-1 的阶乘。
实际上，我们可以把这个显而易见可解决的问题当做是退出条件，然后思考当前问题怎么拆解比较合适。只要分两步，就可以搞定递归算法。

2.从语义的角度看递归

还有一点需要注意，我们要时刻记得递归函数（方法）的功能，以及我们每一步要做的事情，尝试使用语义，会让整个过程更加自然。
例如，我们要求 n 的阶乘 factorial(n)，如果 n 等于 1，就直接返回 1；如果不是 1，我们就讲问题转化为求 n*(n-1) 的阶乘，而 (n-1) 的阶乘正好可以通过函数 factorial(n-1) 求得：

    // 一种更加直观的理解方式
    public static int factorial(int num){
        if (num == 1) {
            return num;
        }
        // 不看做递归调用，仅作为普通函数调用，目的就是求 num-1 的阶乘
        int fact = factorial(num - 1);
        int result = num * fact;    // 求出 num-1 的阶乘，就求出了n的阶乘
        return result;
    }

我们仅从功能的角度调用函数，而不去钻递归的角尖，同样可以写出递归的代码！

3.从栈的角度看递归

还可以把递归想象成是模拟栈的压入，调用一次就相当于将函数压入栈，然后从最后一层开始出栈：

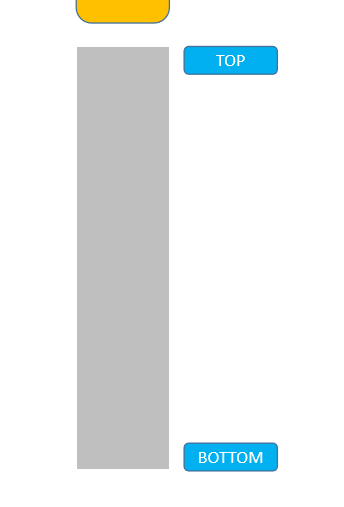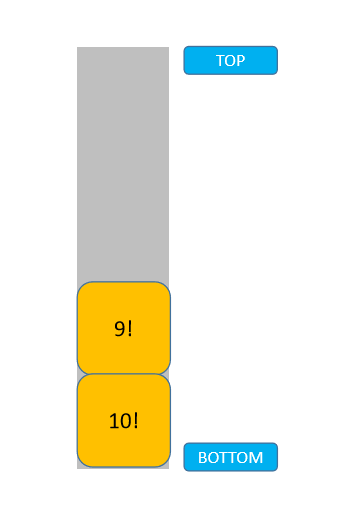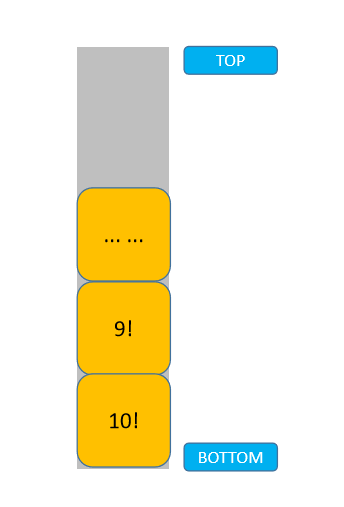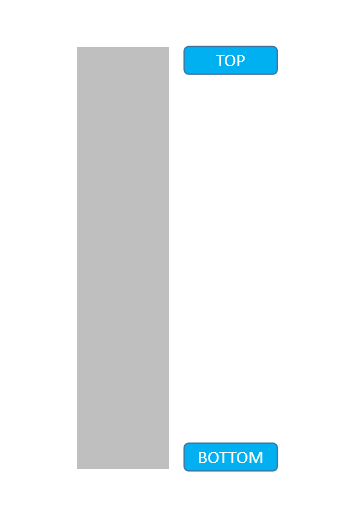
下面我们就再看一个链表的例子，再次强化下对递归的理解。

实例：根据元素值删除链表节点

继续我们之前链表的例子，当时我们只实现了按照索引值删除节点的方法：

    // 移除节点
    public E remove(int index) {
        if (index < 0 || index >= getSize()) throw new IllegalArgumentException("index must > 0 and < size!");
        if (getSize() == 0) throw new IllegalArgumentException("Empty Queue, please enqueue first!");
        // prev节点的初始值为dummyHead
        Node prev = dummyHead;
        // 通过遍历找到prev节点
        for (int i = 0; i < index; i++) prev = prev.next;
        // 储存待删除节点
        Node delNode = prev.next;
        // 跳过delNode
        prev.next = delNode.next;
        // 待删除节点后接null
        delNode.next = null;
        size--;
        return delNode.element;
    }
 
    public E removeFirst() {
        return remove(0);
    }
 
    public E removeLast() {
        return remove(getSize() - 1);
    }

实际上我们还可以根据元素值来删除节点。这里会有一个问题，链表是不限制重复元素的，那么是只删除符合条件的第一个节点，还是删除所有符合条件的节点呢？这里我们选择删除所有符合条件的节点，所以递归就能派上用场了！我们先来看下不使用递归的实现方式：

    // 非递归方式实现
    public void removeElementAll(E element){
        if(isEmpty()) throw new IllegalArgumentException("Empty list, add first!");
        Node prev = dummyHead;
        while (prev.next != null){
            if (prev.next.element == element){
                Node delNode = prev.next;
                prev.next = delNode.next;
                delNode.next = null;
                size--;
            }
            else prev = prev.next;
        }
    }

实现方式很简单，使用 while 循环遍历链表，只要 prev.next 节点的元素值与待删除元素值相等，就删除该节点。
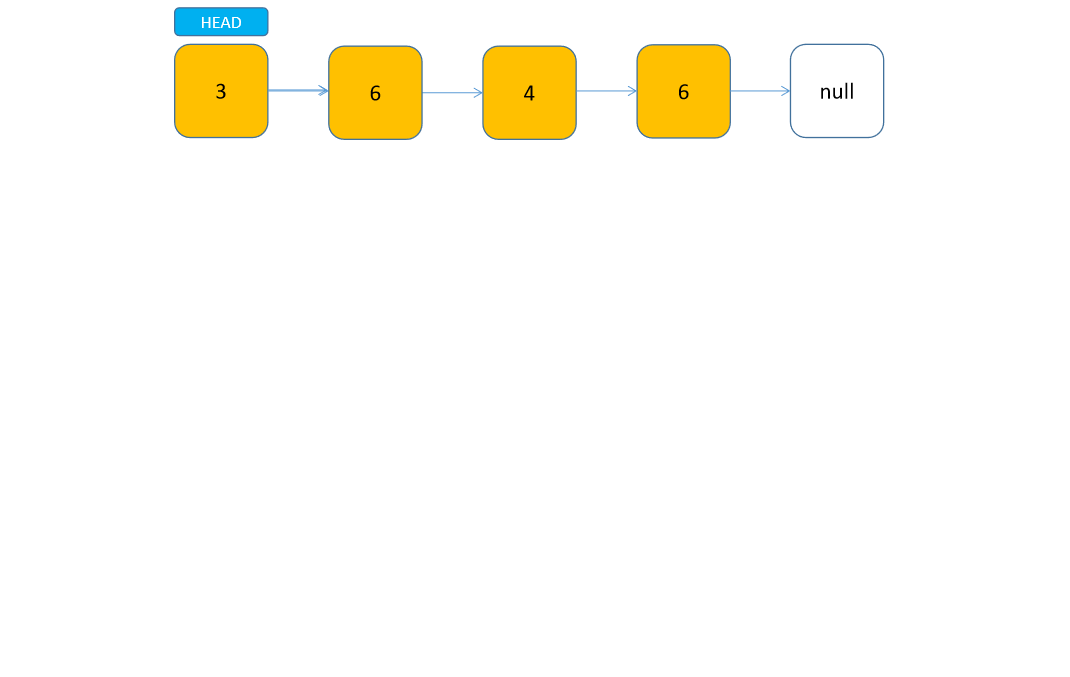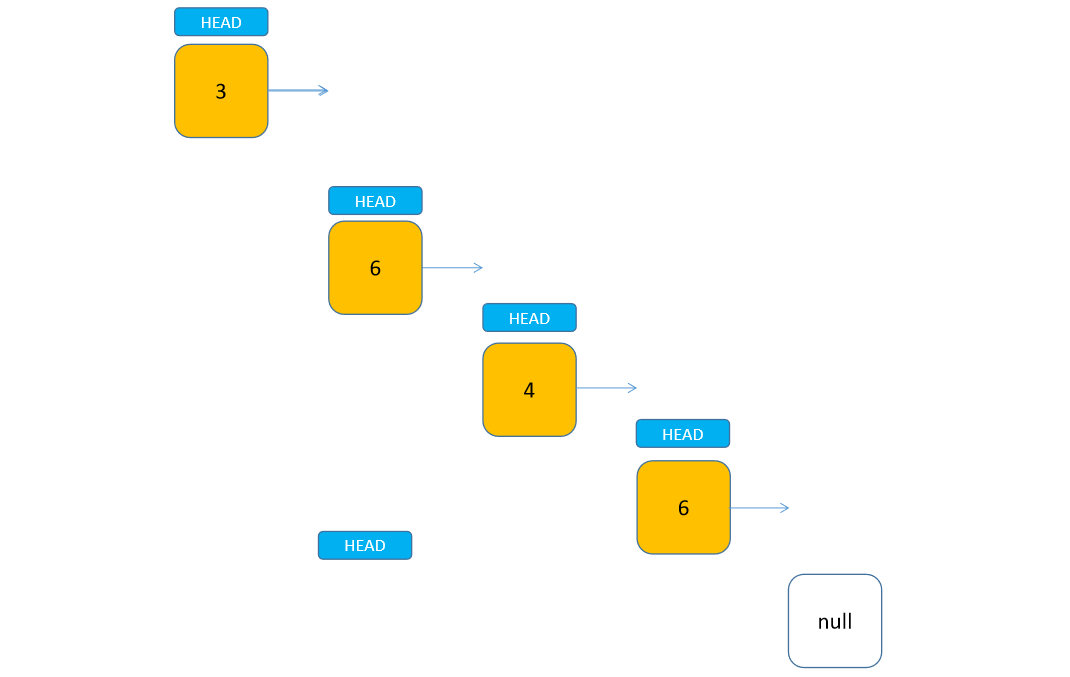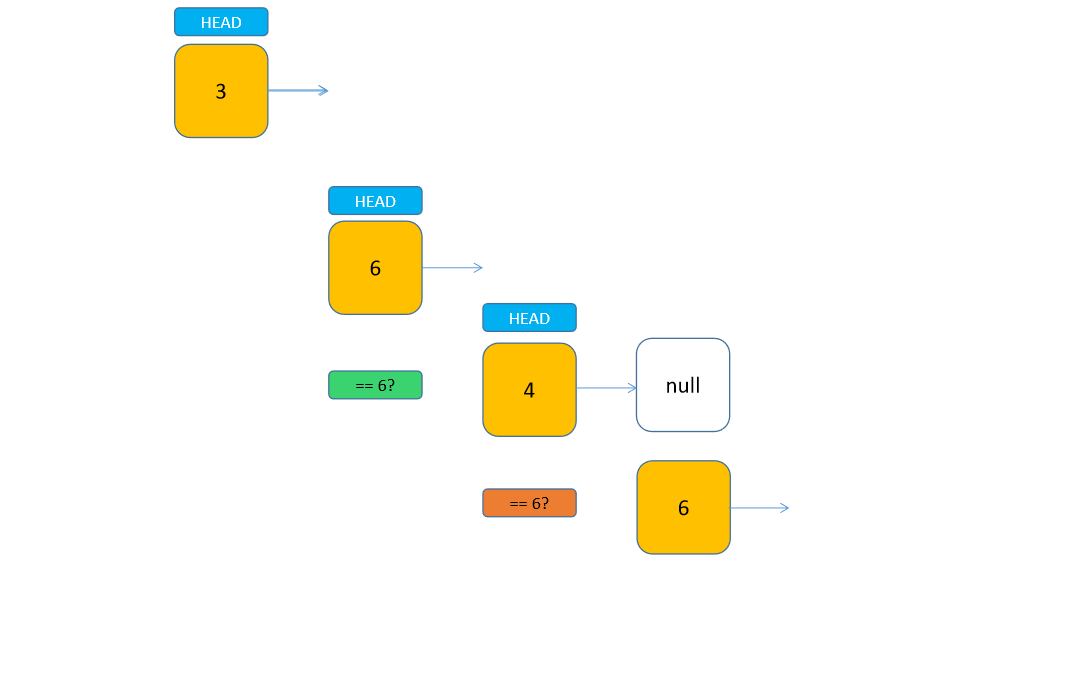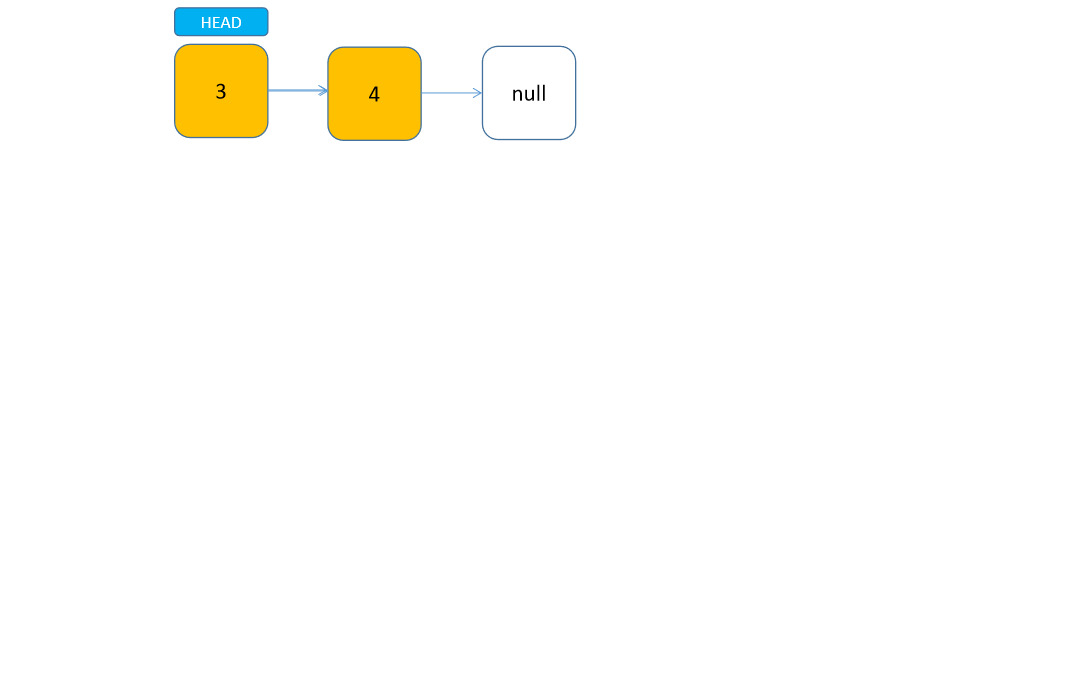
如果采用递归的方式，该如何拆解问题呢？我们无法一下子就找出所有符合条件的节点，但是可以把链表拆解成两部分，一个头节点和一个子链表。这样就把原链表转化成了一个单独的节点和另一个较短的链表。如果节点为空，说明已到链表尾部（显而易见的答案，即退出条件），返回空值即可。例如删除一个链表中所有包含元素6的节点：

public void removeElementAll(E element){
    // 从head开始删除元素，并更新链表
    dummyHead.next = removeElementAll(dummyHead.next, element);
}

private Node removeElementAll(Node head, E element){
    // 如果当前头节点为空，说明链表结束，返回null
    if (head == null) return null;
    // 处理头节点后的子链表并更新
    head.next = removeElementAll(head.next, element);
    // 如果当前头节点为待删除节点，则将头节点的next作为头节点返回
    if (head.element == element) return head.next;
    // 否则返回当前头节点
    return head;
}

这里使用了两个方法，第一个是对外调用的方法，只需要传入要删除的元素值即可。第二个是内部的 private 递归方法，我们结合动图来看，每次子链表往下掉一层，就代表一层递归。可以发现，因为我们的代码是先处理子链表，所以在正向递归的过程中并没有判断当前头节点是否该删除。直到头节点为空时，我们开始向上返回，并开始判断头节点，如果当前头节点为待删除节点，则只返回当前头节点的子链表，否则就连同当前节点一并返回到上一层。通过这样比较直观的过程，应该能够更好地理解递归了。