机器学习 - k-means聚类
k-means简介
k-means是无监督学习下的一种聚类算法,简单说就是不需要数据标签,仅靠特征值就可以将数据分为指定的几类。k-means算法的核心就是通过计算每个数据点与k个质心(或重心)之间的距离,找出与各质心距离最近的点,并将这些点分为该质心所在的簇,从而实现聚类的效果。
k-means具体步骤
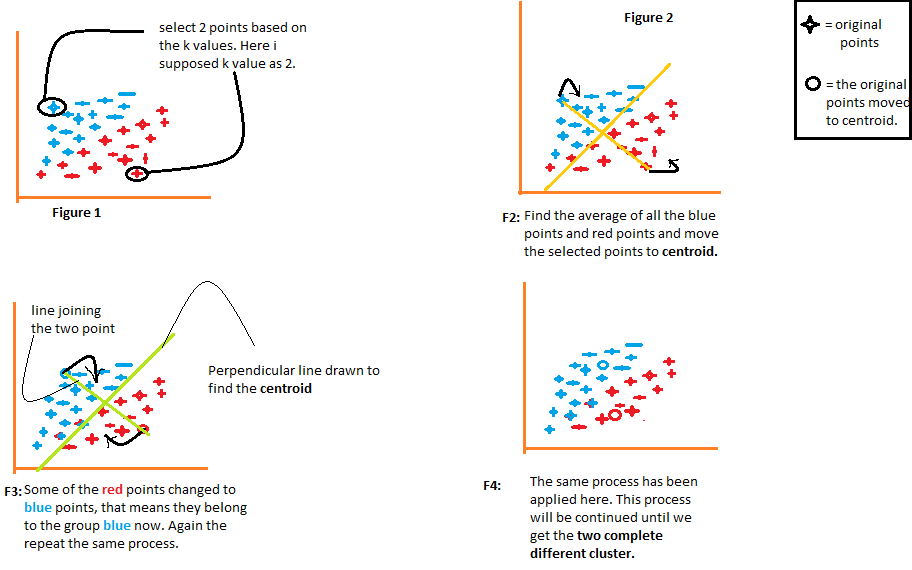
1.指定要把数据聚为几类,确定k值;
2.从数据点中随机选择k个点,作为k个簇的初始质心;
3.计算数据点与各质心之间的距离,并将最近的质心所在的簇作为该数据点所属的簇;
4.计算每个簇的数据点的平均值,并将其作为新的质心;
5.重复步骤2-4,直到所有簇的质心不再发生变化,或达到最大迭代次数。
可以看出,k-means算法的步骤很清晰,而且易于实现。虽然这里的k值感觉像是拍脑袋得到的,但是后面会介绍Elbow方法,通过评估得到合理的k值。我们先来感受一下k-means的效果。
代码实现
import random
import math
import matplotlib.pyplot as plt
class KMeans:
def __init__(self, n_clusters):
self.n_clusters = n_clusters
self.centroid_list = []
self.predict = []
def get_rand_centroid(self, X):
# 随机取质心
centroid_list = []
while len(centroid_list) < self.n_clusters:
d = int(random.random() * len(X))
if X[d] not in centroid_list:
centroid_list.append(X[d])
return centroid_list
@staticmethod
def get_distance(point, C):
# 计算两点间距离(欧式距离)
return math.sqrt((point[0]-C[0])**2 + (point[1]-C[1])**2)
def get_distributed(self, X):
# 计算每个点距离最近的质心,并将该点划入该质心所在的簇
dis_list = [[] for k in range(self.n_clusters)]
for point in X:
distance_list = []
for C in self.centroid_list:
distance_list.append(self.get_distance(point, C))
min_index = distance_list.index(min(distance_list))
dis_list[min_index].append(point)
return dis_list
def get_virtual_centroid(self, distributed):
# 如果有空集,则取其他两个质心的坐标均值
if [] in distributed:
index = distributed.index([])
v_centroid_list = self.centroid_list.copy()
# 去除空集对应的质心
v_centroid_list.pop(index)
# 计算其余两个质心的坐标均值
x = []
y = []
for C in v_centroid_list:
x.append(C[0])
y.append(C[1])
v_centroid_list.insert(index, [round(sum(x) / len(x)), round(sum(y) / len(y))])
else:
# 计算每个簇所有点的坐标的算数平均,作为虚拟质心
v_centroid_list = []
for distribution in distributed:
x = []
y = []
for point in distribution:
x.append(point[0])
y.append(point[1])
v_centroid_list.append([sum(x)/len(x), sum(y)/len(y)])
return v_centroid_list
def fit_predict(self, X):
self.centroid_list = self.get_rand_centroid(X)
while True:
# 聚类
distributed = self.get_distributed(X)
# 计算虚拟质心
v_centroid_list = self.get_virtual_centroid(distributed)
# 如果两次质心相同,说明聚类结果已定
if sorted(v_centroid_list) == sorted(self.centroid_list):
break
# 否则继续训练
self.centroid_list = v_centroid_list
# 对结果按照数据集顺序进行分类
predict = []
for point in X:
i = 0
for dis in distributed:
if point in dis:
predict.append(i)
i += 1
self.predict = predict
return predict
def plot_clustering(self, X):
x = []
y = []
for point in X:
x.append(point[0])
y.append(point[1])
plt.scatter(x, y, c=self.predict, marker='x')
plt.show()
# 样本集合
X = [[0.0888, 0.5885],
[0.1399, 0.8291],
[0.0747, 0.4974],
[0.0983, 0.5772],
[0.1276, 0.5703],
[0.1671, 0.5835],
[0.1306, 0.5276],
[0.1061, 0.5523],
[0.2446, 0.4007],
[0.1670, 0.4770],
[0.2485, 0.4313],
[0.1227, 0.4909],
[0.1240, 0.5668],
[0.1461, 0.5113],
[0.2315, 0.3788],
[0.0494, 0.5590],
[0.1107, 0.4799],
[0.1121, 0.5735],
[0.1007, 0.6318],
[0.2567, 0.4326],
[0.1956, 0.4280]
]
# 初始化kmeans分类器
km = KMeans(3)
# 预测
predict = km.fit_predict(X)
print(predict)
# 绘图
km.plot_clustering(X)
聚类结果如下:
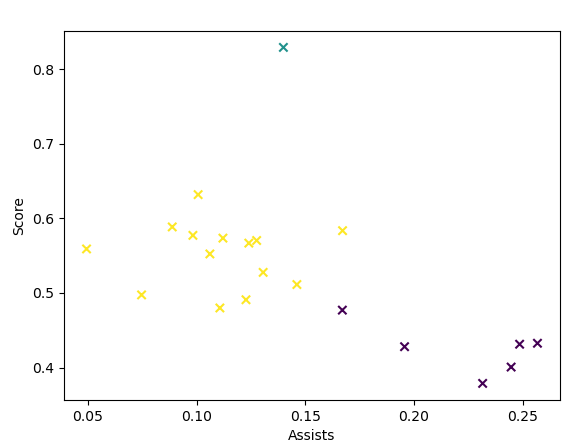
我们采用了几场篮球比赛的球员技术统计数据作为样本,x轴表示助攻数据,y轴表示得分数据,从初步的聚类中,我们可以看出,右下角的一类可看做是助攻很多,而得分较少的球员;左侧这类可看做是助攻较少,但得分相对多一些的球员;而最上面独立的那个类,可看做是得分最多,而且助攻也不少的球员,可理解成MVP球员。这样一来,我们就赋予了这些聚类实际的意义。感觉这个分类结果也挺不错的。
但多跑几次,会发现有时候的分类结果会不太一样,例如没有将MVP球员作为单独的一类:
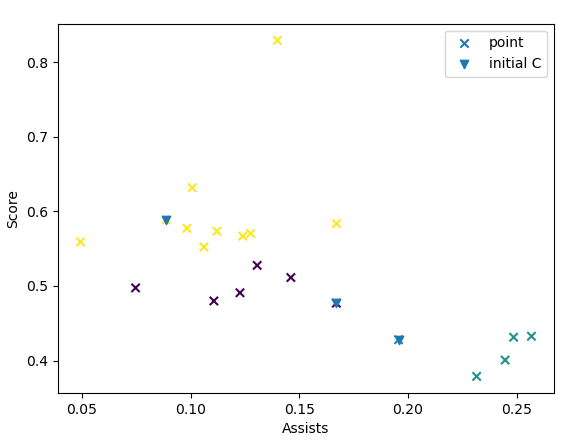
可以看出,如果首次随机出的质心挨得太近,会导致分类结果不理想(蓝色向下的箭头表示随机的初始质心)。
k-means++
为了解决初始质心不合理而导致分类不准确的问题,我们可以优化质心初始化的步骤,使各个质心相距尽可能的远。k-means++ 算法就是一种为 k-means 寻找初始化质心的算法。它由David Arthur 和 Sergei Vassilvitskii 于2007年提出(论文地址),主要是对之前步骤1进行进一步优化,具体步骤如下:
1a.随机选出一个点作为质心;
1b.通过计算概率,得到新的质心。其中概率的计算方法如下:
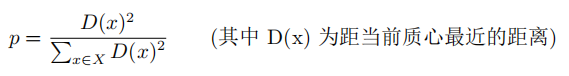
1c.重复1b步,直到凑齐k个质心。
注:原作论文中并未提及如何根据概率值选择质心,我看网上有很多文章使用了“轮盘法”挑选质心,就是计算出各点的概率后,再计算出各点的累计概率值,然后随机一个概率值r,将r落入累计概率区间对应的点作为质心。这里就粗暴一点,直接选取概率最大的那个点(与当前质心最远的点)作为质心。
def k_means_plus(self, X):
centroid_list = []
# 随机选出第一个点
random_1 = int(random.random() * len(X))
centroid_list.append(X[random_1])
while len(centroid_list) < self.n_clusters:
distance_list = []
for x in X:
tmp_list = []
for C in centroid_list:
tmp_list.append(pow(self.get_distance(x, C), 2))
# 取距离当前质心最近的距离D(X)^2
distance_list.append(min(tmp_list))
# 选取D(X)^2最大的点作为下个质心(概率计算公式中分母相同,可略去)
max_index = distance_list.index(max(distance_list))
centroid_list.append(X[max_index])
return centroid_list
直接拿这个函数替换之前的get_rand_centroid()方法即可。聚类效果如下:
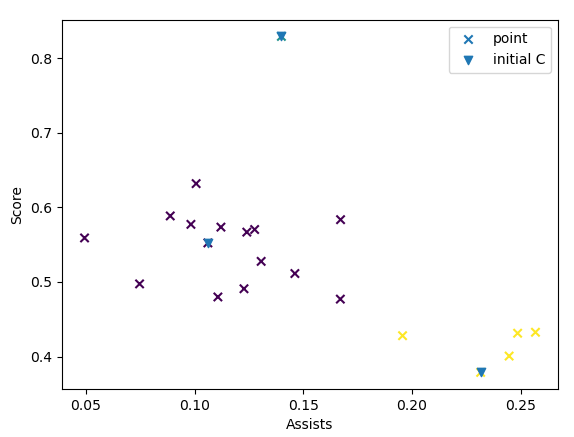
三个初始质心都有较远的距离,从而保证了聚类的准确性。
WCSS - k-means算法的评估标准
由于k-means是一种无监督学习方法,没有一种严格的标准来衡量聚类结果的性能,大部分情况下都是根据人的经验来判断,但是如果数据超过三维,无法可视化的话,就比较尴尬了。所以还是需要有一种方法能够评估k-means的性能。之前不是通过计算距离选取质心吗,我们便可以用所有点到其所属质心的距离加和作为一种衡量方式,这就是WCSS方法(Within-Cluster Sum of Squares),WCSS方法可以将性能进行量化,对于相同的k,WCSS越小,代表总体性能越好。所以我们可以进行N轮训练,取WCSS最小的那个作为最终的聚类。
直接在fit_predict()方法中加入WCSS的计算即可:
def fit_predict(self, X, N=10):
# 进行N轮训练(默认进行10轮)
train_num = 0
# 存放质心与聚类结果
WCSS_dict = {}
while train_num < N:
# self.centroid_list = self.get_rand_centroid(X)
# 使用k-means++算法选出初始质心
self.centroid_list = self.k_means_plus(X)
# 记录初始质心
self.initial_list = self.centroid_list
while True:
# 聚类
distributed = self.get_distributed(X)
# 计算虚拟质心
v_centroid_list = self.get_virtual_centroid(distributed)
# 如果两次质心相同,说明聚类结果已定
if sorted(v_centroid_list) == sorted(self.centroid_list):
break
# 否则继续训练
self.centroid_list = v_centroid_list
# 对结果按照数据集顺序进行分类
predict = []
WCSS = 0
for point in X:
i = 0
for dis in distributed:
if point in dis:
predict.append(i)
# 计算当前点到其质心的距离,平方后再累加到WCSS中
WCSS += pow(self.get_distance(point, self.centroid_list[i]), 2)
i += 1
WCSS_dict[WCSS] = [self.centroid_list, predict]
print("第" + str(train_num+1) + "轮的WCSS为:" + str(WCSS))
train_num += 1
# 选出WCSS最小的那个作为最终的聚类
min_WCSS = min(WCSS_dict.keys())
last_predict = WCSS_dict[min_WCSS][1]
self.predict = last_predict
return last_predict, min_WCSS
# 执行结果:
第1轮的WCSS为:0.04830321200000001
第2轮的WCSS为:0.04830321200000001
第3轮的WCSS为:0.04830321200000001
第4轮的WCSS为:0.04830321200000001
第5轮的WCSS为:0.04751589380952381
第6轮的WCSS为:0.04830321200000001
第7轮的WCSS为:0.04751589380952381
第8轮的WCSS为:0.04830321200000001
第9轮的WCSS为:0.04751589380952381
第10轮的WCSS为:0.04830321200000001
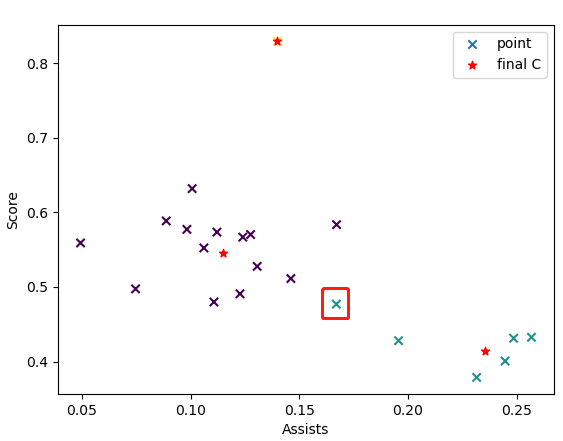
图中用红框标出的点,之前被归为得分较出色的球员,现在被归为了助攻较出色的球员。(红色的*点标注的是最终的质心)
Elbow方法 - 确定k的好办法
最后,我们再来讲一下关于k的取值问题。随着k的增大,即质心的增多,整体的WCSS是逐渐减小的(因为每个点能找到与其距离更近的质心的概率变大了),所以我们可以通过不断增大k,来观察整体的性能:
def elbow(self, k_range=10):
# 通过elbow方法选择最佳k值
x = []
y = []
for k in range(1, k_range+1):
self.n_clusters = k
x.append(k)
# 取出不同k值下的WCSS
_, min_WCSS = self.fit_predict(X)
y.append(min_WCSS)
plt.plot(x, y)
plt.xlabel('k')
plt.ylabel('WCSS')
plt.show()

从图中可以发现,k从1到4的过程中,聚类性能有着明显的提升,但是再继续增加聚类的个数,性能提升的幅度就没有之前那么明显了,而且,聚类个数太多,也会让数据集变得过于分散,所以,在本例中,k=4是较好的选择。说明一开始根据经验取的k=3并不是最优的。我们再跑一下k=4的聚类:
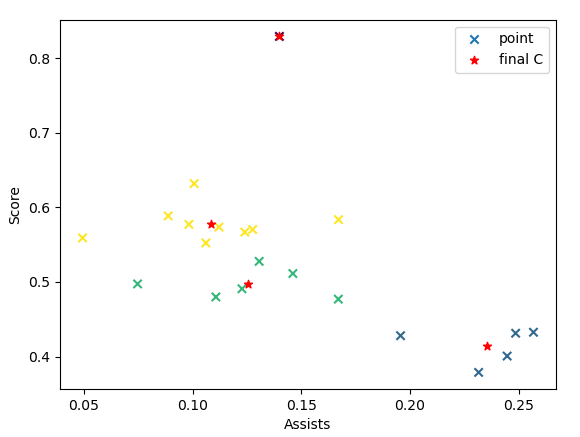
通过最终的聚类,我们发现,算法将之前得分较多的球员又细分为了两类,黄色这类的得分要比绿色这类更高,所以可看做是真正得分多的球员;而绿色这类的得分并不出众,助攻也不算高,可看做是表现较为一般的球员(毕竟不可能所有的球员都有好的表现)。这样的分类从整体来看也更加符合实际情况。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号