XNA Primitives画线 1（2D和向量反射）

    由于学习XNA的时间很仓促，加上以前也没有图形学的基础知识，所以我对Primitives的东西也了解的少。下面就主要讲下我昨天和今天做的东西。

    第一个是在2D平面上画出XY坐标、和以坐标原点（0，0）[这里实际是屏幕的中心]……看到的是下图的效果：

 

 

 

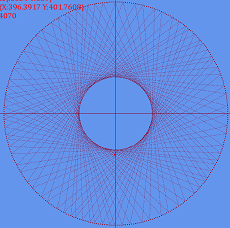
    我做的第一个DEMO是用SpriteBatch的Draw方法。SpriteBatch没有提供如GDI中的画线、画圆、画矩形一类的方法，关于绘制就只有一个Draw方法，Draw方法的绘制对像是一个Texture2D对像。 经过我简单的分析，在这个例子中所有的线（包括图中的坐标轴的圆）都是由一个一个的点构成的。

    如：添加屏幕坐标元素： 

 

 1private void DrawCoordinate() 
 2{ 
 3    for (int i = 0; i < Window.ClientBounds.Width;i++ ) 
 4    { 
 5        pointCoordinate.Add(new Vector2(0f + i, Window.ClientBounds.Height / 2)); 
 6    } 
 7
 8    for (int i = 0; i < Window.ClientBounds.Height; i++) 
 9    { 
        pointCoordinate.Add(new Vector2(Window.ClientBounds.Width / 2, 0 + i)); 
    } 
} 

 

    绘制圆：

 

 

 1private void DrawCircle() 
 2{ 
 3    Matrix matrix; 
 4    for (int i = 0; i < 360; i++) 
 5    { 
 6        matrix = new Matrix 
 7          ((float)Math.Cos(MathHelper.ToRadians(i)), (float)Math.Sin(MathHelper.ToRadians(i)), 0, 0, 
 8          -1 * (float)Math.Sin(MathHelper.ToRadians(i)), (float)Math.Cos(MathHelper.ToRadians(i)), 0, 0, 
 9          0, 0, 0, 0, 
          0, 0, 0, 0 
          ); 
       spriteBatch.Draw(texture, Wc.TransformToWindowCoordinate(Vector2.Transform(new Vector2(280, 0), matrix) ), new Rectangle(10, 20, 2, 2), Color.YellowGreen); 
    } 
} 

 

    这里要说明一下，我们通过new Vector2(280, 0)定义了一个起始的2D坐标，matrix是旋转变换矩阵，它实质上是2*2格式的，因为要实现2向量的旋转，一个2*2的矩阵就可以满足了。但是XNA中好像没有对2*2的矩阵定义，所有我只有用了代码里的方法。

    我们将圆中间的线的存储在List<Vector2> 类型的pointPosi对像中，DEMO的Update内容如下：

 

if (280 - Position.Length() < 1) 
{ 
    Vector2 tmp = Position; 
    tmp.Normalize(); 
    velocity = Vector2.Reflect(velocity, tmp); 
} 
Position += velocity; 
pointPosi.Add(Position);

 

    在这里，我们先判断点的长度是否到达了圆的边界上，如果到了，我们就要根据这里的速度向量和这个点的向量算出一个反射出来的速度向量，在每次Update的过程中我们都要向点集合中加入一个新的点。

    现在我们来说下求反射角。这之前我没注意到XNA已经提供了求反射向量的方法Vector2.Reflect( , )，所以就想自己写个方法，在网上找了些资料，但看了半天都没年出过所以然。所以就自己去分析，下面就来简单的说下：

 

    向量a是入射的速度向量，向量b是反射的速度向量，p是向量OA和向量a的夹角。

    如果说入射向量是CA，那么反射向量就是AD，AD＝AC+BC+BD＝－CA+2BC，由于BC＝CA+AB，所以：AD＝－CA++2（CA+AB），现在就重要的是求微量AB，因为其它的都是已知的。现在就要用到夹角p了，那怎么知道p的大小呢？在三角形ABC中，我们只知道向量CA， BA和BC都不知道。

    可能已经有人看出来了，我们还有个向量OA。在这里我们完全可以把一个向量看作是一个只代表方向的向量和一个只代表大小的标量的积，就如速率是由速度和方向和积得来的一样（因为我这用了向量做速率，所以一下子就想到这了），这个向量的大小其实就是这处向量的模长,得出两个"纯方向"向量后我们就会发现它们再次求模的比值就是Cos p。由此，cos p=OA.Normalize().Length()/CA.Normalize().Length() ……接下来就交给愿意去推算的人去推算吧。

    当然所以的推算结果出来后，就有一个固定的方法：

 

 

public Vector2 Reflect(Vector2 vector, Vector2 normal) 
{ 
    Vector2 vector2; 
    float num = (vector.X * normal.X) + (vector.Y * normal.Y); 
    vector2.X = vector.X - ((2f * num) * normal.X); 
    vector2.Y = vector.Y - ((2f * num) * normal.Y); 
    return vector2; 
} 

 

    如果是3D空间的话就是：

 

 1public Vector3 Reflect(Vector3 vector, Vector3 normal) 
 2{ 
 3    Vector3 vector2; 
 4    float num = ((vector.X * normal.X) + (vector.Y * normal.Y)) + (vector.Z * normal.Z); 
 5    vector2.X = vector.X - ((2f * num) * normal.X); 
 6    vector2.Y = vector.Y - ((2f * num) * normal.Y); 
 7    vector2.Z = vector.Z - ((2f * num) * normal.Z); 
 8    return vector2; 
 9}