小胖守皇宫——树形DP
题干
huyichen世子事件后,xuzhenyi成了皇上特聘的御前一品侍卫。
皇宫以午门为起点,直到后宫嫔妃们的寝宫,呈一棵树的形状;有边相连的宫殿间可以互相望见。大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是xuzhenyi手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助xuzhenyi布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
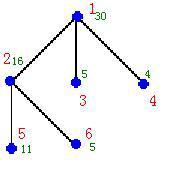
输入文件中数据表示一棵树,描述如下:
第1行n,表示树中结点的数目。
第2行至第n+1行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号i(0<i<=n),在该宫殿安置侍卫所需的经费k,该边的儿子数m,接下来m个数,分别是这个节点的m个儿子的标号r1,r2,r3......,rm
对于一个n(0 < n <= 1500)个结点的树,结点标号在1到n之间,且标号不重复。
输出文件仅包含一个数,为所求的最少的经费。
样例
Input:
6 1 30 3 2 3 4 2 16 2 5 6 3 5 0 4 4 0 5 11 0 6 5 0
Output:25
翻译
一个点可以看守它自己和其它所有邻接点,每一个点放置守卫都有不同的费用,现在询问将所有邻接点看守所需要的最小费用
题解
问题很明显是一个树形动态规划。
问整棵树最优方案,我们可以拆解为根费用+各个子树最优的费用。子问题可以拆解。所以可以使用动态规划。
一个点被守卫可以有三种选择:一,自己守卫自己。二,父亲节点来守卫自己。三,儿子节点来守卫自己。
定义dp[u][0]:u自己守护自己的情况下,以u为根的子树中所需要的最小费用
定义dp[u][1]:u父亲守护自己的情况下,以u为根的子树中所需要的最小费用,默认自己就不安置守卫了。
定义dp[u][2]:u儿子守护自己的情况下,以u为根的子树中所需要的最小费用,默认自己就不安置守卫了。
现在分别来分析三种情况:注意这时候,我们考虑的是以u为根的子树,这样一个子问题
一,u自己守卫u自己。 dp[u][0]
这时候,u已经满足守卫条件,那么它的儿子v们,无论是自己守护自己,让父亲u守护自己,还是让v自己的儿子守护自己,都是可以的,都满足条件。
即dp[u][0]最优情况就是:挑选dp[v][0],dp[v][1],dp[v][2]三种情况中最优的一个,再加上u自己守护自己的费用:money[u]即可。
即动态转移方程一:dp[u][0] = money[u] + min ( dp[v][0] , dp[v][1] , dp[v][2] ) ;
实际操作的时候,由于儿子v多个,所以应该这样做
dp[u][0] += money[u];
for ( u所有儿子 ) dp[u][0] += min ( dp[v][0] , dp[v][1] , dp[v][2] )
二,u父亲守卫u自己。 dp[u][1]
这时候,u被父亲守卫,且u本身是不安置守卫的。那么u的儿子们v怎么办呢?父亲u靠不住了,只能v自己来守卫自己,或者v让v的儿子守卫自己。
即dp[u][1]最优情况就是:挑选dp[v][0]和dp[v][2]中最优的一个。注意这时候,因为u本身没有放置守卫,所以不加上money[u]。
即动态转移方程二:dp[u][1] = min ( dp[v][0] , dp[v][2] ) ;
实际操作的时候,由于儿子v多个,所以应该这样做
for ( u所有儿子 ) dp[u][1] += min ( dp[v][0] , dp[v][2] ) ;
三,u儿子守卫u自己。dp[u][2]
这时候,u被儿子守卫,且u本身是不安置守卫的。
而对于u的儿子们v来说,父亲u不守卫v,那么v只能自力更生或者再让v的儿子守卫自己。
所以v的选择:0,或者2,两种选择。选择其中较优的那个。
而对于u本身来说,u的儿子可能不止一个,那么只要其中有一个儿子放置了守卫,那么u就可以被守卫到,就满足要求。
如果说有儿子v:dp[v][0] < dp[v][2] ,即有儿子会去选择自己放置守卫,那问题自然好说了。
如果说这样的儿子有多个,那么选择最优的那个即可。
但问题是,万一所有的v,都是dp[v][2] < dp[v][0],也就是所有的儿子v都选择了让v的儿子守卫v自己,那就没有任何一个v来自己放置守卫进而看守u了!
也就是u可能会出现没人看管的情况。
这时候,总要有一个儿子v去承担这个责任,意思就是,总要有一个v去亏损一部分费用,不去选择dp[v][2],而是去选择dp[v][0]。
那,为了保持全局最优,我们必须让一个亏损最少的儿子v去承担这个责任,意思就是,需要找一个tot = dp[v][0] - dp[v][2] 最小的儿子v去。
原理明白了,那么第三条转移方程就好说了。但是需要加一些东西
dp[u][2] += min ( dp[v][0] , dp[v][2] ) ;//仍然是转移
tot = min ( tot , dp[v][0] - dp[v][2] ) ;
这里定义了一个tot,就是那个亏损的差值。
在for(u的每一个儿子v) 当中,每操作一个,我们就用min更新一下那个差值tot,以保证跳出for循环的时候,我们记录到的tot值是最小的 。
跳出循环后:
if (tot > 0 ) dp[u][2] += tot ;
这句话什么意思?
首先,if ( tot>0 )意思就是tot必须大于零的时候才执行。
如果说tot是<=0的情况,那么意思就是之前for循环的时候,出现了儿子本身 dp[v][0] <= dp[v][2] 的情况,意思就是会自动有v在自己那里放置守卫。
这个情况下,这个tot差值是没有用处的。
只有循环完一整遍之后,发现tot还大于0 ,(就是没有任何一个儿子是孝顺的) 这时候我们才需要用tot进行调整。
这时候,tot记录的那个正值,就是其中那个亏损最小的儿子亏损的费用。
由于在for里面那个 dp[u][2] += min ( dp[v][0] , dp[v][2] ) ;
动态转移方程中,每一次每一次都选择了dp[v][0],所以最后,我们把dp[u][0]加上tot,就相当于把其中那个亏损最小的儿子v由dp[v][0]变成了dp[v][2]。
这时候,问题就解决了。
四,最后输出
输出的时候要选择根节点 dp[root][0] 和 dp[root][2]里面小的那个。当然一整棵树的根节点是没有父亲的,所以没有 dp[root][1]考虑在内。
代码
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 const int maxn=1500+1; 5 const int Inf=0x3f3f3f3f; 6 int n,root,money[maxn],dp[maxn][3]; 7 8 //前向星 9 struct Edge{int to,next;}e[maxn]; 10 int Head[maxn],len; 11 void Insert(int x,int y){ 12 e[++len].to=y; 13 e[len].next=Head[x]; 14 Head[x]=len; 15 } 16 17 //读入函数 18 void Read(){ 19 scanf("%d",&n); 20 root=1; 21 for(int i=1;i<=n;i++){ 22 int num,p,m;scanf("%d%d%d",&num,&p,&m); 23 money[num]=p; 24 int son=0; 25 for(int j=1;j<=m;j++){ 26 if(son==root)root=num;//小技巧快速找到根root 27 scanf("%d",&son); 28 Insert(num,son); 29 } 30 } 31 } 32 33 //操作函数 34 void Dfs(int u){ 35 dp[u][0]=money[u]; 36 //dp[u][0]在循环外边加上一个money[u] 37 //进入for循环的时候就不会加上好几遍了 38 int tot=Inf; 39 for(int i=Head[u];i;i=e[i].next){ 40 int v=e[i].to; 41 Dfs(v); 42 dp[u][0]+=std::min(dp[v][0],std::min(dp[v][1],dp[v][2])); 44 dp[u][1]+=std::min(dp[v][0],dp[v][2]); 45 dp[u][2]+=std::min(dp[v][0],dp[v][2]); 46 tot=std::min(tot,dp[v][0]-dp[v][2]); 47 } 48 if(tot>0)dp[u][2]+=tot; 49 } 50 51 //输出函数 52 void Out(){ 53 printf("%d",std::min(dp[root][0],dp[root][2])); 54 } 55 56 int main(){ 57 Read(); 58 Dfs(root); 59 Out(); 60 return 0; 61 }
最近在学习树形dp,这样一个比较经典的题还是值得掌握的。
祝AC。


