python数字图像处理（18）：高级形态学处理

形态学处理，除了最基本的膨胀、腐蚀、开/闭运算、黑/白帽处理外，还有一些更高级的运用，如凸包，连通区域标记，删除小块区域等。

1、凸包

凸包是指一个凸多边形，这个凸多边形将图片中所有的白色像素点都包含在内。

函数为：

skimage.morphology.convex_hull_image(image)

输入为二值图像，输出一个逻辑二值图像。在凸包内的点为True, 否则为False

例：

import matplotlib.pyplot as plt
from skimage import data,color,morphology

#生成二值测试图像
img=color.rgb2gray(data.horse())
img=(img<0.5)*1

chull = morphology.convex_hull_image(img)

#绘制轮廓
fig, axes = plt.subplots(1,2,figsize=(8,8))
ax0, ax1= axes.ravel()
ax0.imshow(img,plt.cm.gray)
ax0.set_title('original image')

ax1.imshow(chull,plt.cm.gray)
ax1.set_title('convex_hull image')

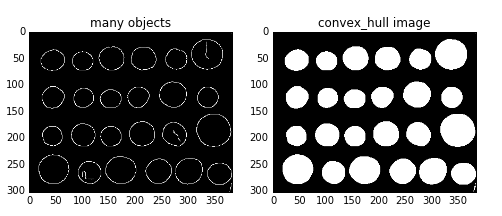
convex_hull_image()是将图片中的所有目标看作一个整体，因此计算出来只有一个最小凸多边形。如果图中有多个目标物体，每一个物体需要计算一个最小凸多边形，则需要使用convex_hull_object（）函数。

函数格式：skimage.morphology.convex_hull_object(image, neighbors=8)

输入参数image是一个二值图像，neighbors表示是采用4连通还是8连通，默认为8连通。

例：

import matplotlib.pyplot as plt
from skimage import data,color,morphology,feature

#生成二值测试图像
img=color.rgb2gray(data.coins())
#检测canny边缘,得到二值图片
edgs=feature.canny(img, sigma=3, low_threshold=10, high_threshold=50) 

chull = morphology.convex_hull_object(edgs)

#绘制轮廓
fig, axes = plt.subplots(1,2,figsize=(8,8))
ax0, ax1= axes.ravel()
ax0.imshow(edgs,plt.cm.gray)
ax0.set_title('many objects')
ax1.imshow(chull,plt.cm.gray)
ax1.set_title('convex_hull image')
plt.show()

2、连通区域标记

在二值图像中，如果两个像素点相邻且值相同（同为0或同为1），那么就认为这两个像素点在一个相互连通的区域内。而同一个连通区域的所有像素点，都用同一个数值来进行标记，这个过程就叫连通区域标记。在判断两个像素是否相邻时，我们通常采用4连通或8连通判断。在图像中，最小的单位是像素，每个像素周围有8个邻接像素，常见的邻接关系有2种：4邻接与8邻接。4邻接一共4个点，即上下左右，如下左图所示。8邻接的点一共有8个，包括了对角线位置的点，如下右图所示。

在skimage包中，我们采用measure子模块下的label（）函数来实现连通区域标记。

函数格式：

skimage.measure.label（image,connectivity=None)

参数中的image表示需要处理的二值图像，connectivity表示连接的模式，1代表4邻接，2代表8邻接。

输出一个标记数组（labels), 从0开始标记。

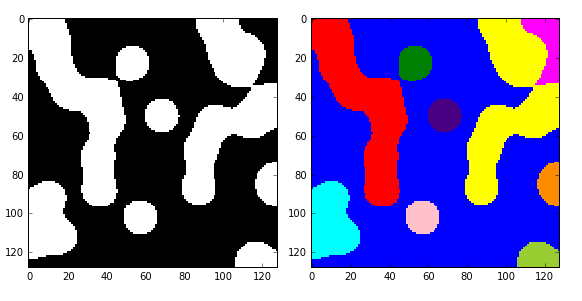
import numpy as np
import scipy.ndimage as ndi
from skimage import measure,color
import matplotlib.pyplot as plt

#编写一个函数来生成原始二值图像
def microstructure(l=256):
    n = 5
    x, y = np.ogrid[0:l, 0:l]  #生成网络
    mask = np.zeros((l, l))
    generator = np.random.RandomState(1)  #随机数种子
    points = l * generator.rand(2, n**2)
    mask[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1
    mask = ndi.gaussian_filter(mask, sigma=l/(4.*n)) #高斯滤波
    return mask > mask.mean()

data = microstructure(l=128)*1 #生成测试图片

labels=measure.label(data,connectivity=2)  #8连通区域标记
dst=color.label2rgb(labels)  #根据不同的标记显示不同的颜色
print('regions number:',labels.max()+1)  #显示连通区域块数(从0开始标记)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
ax1.imshow(data, plt.cm.gray, interpolation='nearest')
ax1.axis('off')
ax2.imshow(dst,interpolation='nearest')
ax2.axis('off')

fig.tight_layout()
plt.show()

在代码中，有些地方乘以1，则可以将bool数组快速地转换为int数组。

结果如图：有10个连通的区域，标记为0-9

如果想分别对每一个连通区域进行操作，比如计算面积、外接矩形、凸包面积等，则需要调用measure子模块的regionprops（）函数。该函数格式为：

skimage.measure.regionprops(label_image)

返回所有连通区块的属性列表，常用的属性列表如下表：

属性名称	类型	描述
area	int	区域内像素点总数
bbox	tuple	边界外接框(min_row, min_col, max_row, max_col)
centroid	array	质心坐标
convex_area	int	凸包内像素点总数
convex_image	ndarray	和边界外接框同大小的凸包
coords	ndarray	区域内像素点坐标
Eccentricity	float	离心率
equivalent_diameter	float	和区域面积相同的圆的直径
euler_number	int	区域欧拉数
extent	float	区域面积和边界外接框面积的比率
filled_area	int	区域和外接框之间填充的像素点总数
perimeter	float	区域周长
label	int	区域标记

 

3、删除小块区域

有些时候，我们只需要一些大块区域，那些零散的、小块的区域，我们就需要删除掉，则可以使用morphology子模块的remove_small_objects（)函数。

函数格式：skimage.morphology.remove_small_objects(ar, min_size=64, connectivity=1, in_place=False)

参数：

ar: 待操作的bool型数组。

min_size: 最小连通区域尺寸，小于该尺寸的都将被删除。默认为64.

connectivity: 邻接模式，1表示4邻接，2表示8邻接

in_place: bool型值，如果为True,表示直接在输入图像中删除小块区域，否则进行复制后再删除。默认为False.

返回删除了小块区域的二值图像。

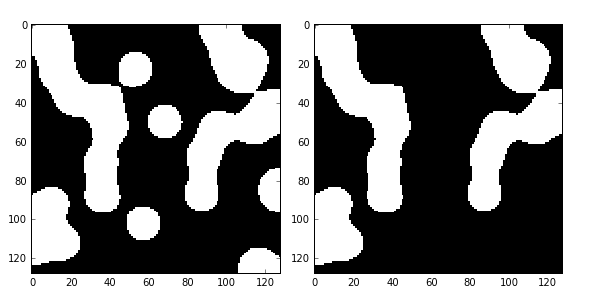
import numpy as np
import scipy.ndimage as ndi
from skimage import morphology
import matplotlib.pyplot as plt

#编写一个函数来生成原始二值图像
def microstructure(l=256):
    n = 5
    x, y = np.ogrid[0:l, 0:l]  #生成网络
    mask = np.zeros((l, l))
    generator = np.random.RandomState(1)  #随机数种子
    points = l * generator.rand(2, n**2)
    mask[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1
    mask = ndi.gaussian_filter(mask, sigma=l/(4.*n)) #高斯滤波
    return mask > mask.mean()

data = microstructure(l=128) #生成测试图片

dst=morphology.remove_small_objects(data,min_size=300,connectivity=1)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
ax1.imshow(data, plt.cm.gray, interpolation='nearest')
ax2.imshow(dst,plt.cm.gray,interpolation='nearest')

fig.tight_layout()
plt.show()

在此例中，我们将面积小于300的小块区域删除（由1变为0），结果如下图：

 

 4、综合示例：阈值分割+闭运算+连通区域标记+删除小区块+分色显示

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from skimage import data,filter,segmentation,measure,morphology,color

#加载并裁剪硬币图片
image = data.coins()[50:-50, 50:-50]

thresh =filter.threshold_otsu(image) #阈值分割
bw =morphology.closing(image > thresh, morphology.square(3)) #闭运算

cleared = bw.copy()  #复制
segmentation.clear_border(cleared)  #清除与边界相连的目标物

label_image =measure.label(cleared)  #连通区域标记
borders = np.logical_xor(bw, cleared) #异或
label_image[borders] = -1
image_label_overlay =color.label2rgb(label_image, image=image) #不同标记用不同颜色显示

fig,(ax0,ax1)= plt.subplots(1,2, figsize=(8, 6))
ax0.imshow(cleared,plt.cm.gray)
ax1.imshow(image_label_overlay)

for region in measure.regionprops(label_image): #循环得到每一个连通区域属性集
    
    #忽略小区域
    if region.area < 100:
        continue

    #绘制外包矩形
    minr, minc, maxr, maxc = region.bbox
    rect = mpatches.Rectangle((minc, minr), maxc - minc, maxr - minr,
                              fill=False, edgecolor='red', linewidth=2)
    ax1.add_patch(rect)
fig.tight_layout()
plt.show()