判断C语言的算术运算越界问题
大量的安全漏洞是由于计算机算术运算的微妙细节引起的, 具体的C语言, 诸如符号数和无符号数之间转换, 算术运算的越界都会导致不可预知的错误和安全漏洞, 具体的案例数不胜数.
作为一个系统程序员, 有必要对这些细节有深入的了解. 本篇参考csapp, 主要介绍如何判断算术运算的越界问题.
(虽然本篇的代码经过大量的测试, 但本人仍然无法保证代码的正确性, 希望大家纠错).
讲解的原则是"摆定理, 不证明, 写代码". 具体的证明过程在csapp中有详细的讲解, 也不是太难. 主要使用关键定理来写代码. Go~
☞问题一: 无符号数的加法越界问题
[定理]
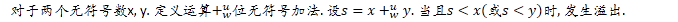
[理解]
这个定理比较容易, 也比较能让人接受. 不解释啦.
[代码]
1 /* Determine whether arguments can be added without overflow */ 2 3 int uadd_ok(unsigned int x, unsigned int y) 4 5 { 6 7 return !(x+y < x); 8 9 }
☞问题二: 无符号数的减法越界问题
[定理]
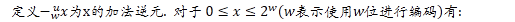
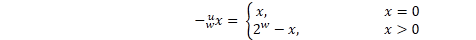
[理解]
1. 计算机中没有减法, x-y = x+(-y), 这里的-y就是上述的y的加法逆元. 不管是有符号还是无符号, 都是转换为加法运算. 只是加法逆元的定义不同.
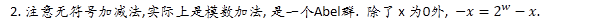
3. C语言保证 -x = ~x+1; 可以验证这种方式与上面公式等价.
4. s=x-y = x+(-y). 那么 不会溢出 等价于 y不为0 或者 !uadd_ok(x, -y).
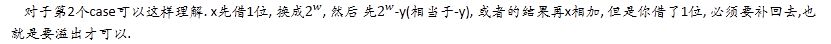
[代码]
1 /* Determine whether argumnts can be substracted without overflow */ 2 3 int usub_ok(unsigned int x, unsigned int y) 4 5 { 6 7 return !y || !uadd_ok(x, -y); 8 9 }
☞问题三: 无符号数的乘法越界问题
[定理]

[理解]
等价条件可以相互推导即可.
[代码]
1 /* Determine whether arguments can be multiplied without overflow */ 2 3 int umul_ok(unsigned int x, unsigned int y) 4 5 { 6 7 unsigned int p = x * y; 8 9 return !x || p/x==y; 10 11 }
☞问题四: 有符号数的加法越界问题
[定理]
对于两个有符号数x, y. 越界的等价条件是x,y为负数, x+y为正数或者x,y为正数, x+y为负数.
[理解]
这个定理比较容易.
[代码]
1 /* Determine whether arguments can be added without overflow */ 2 3 int tadd_ok(int x, int y) 4 5 { 6 7 return !(x<0&&y<0&&x+y>0 || x>0&&y>0&&x+y<0); 8 9 }
☞问题五: 有符号数的减法越界问题
[定理]
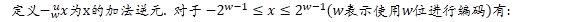
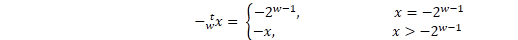
[理解]
同无符号的减法一样, 只是加法逆元的定义不同, 但是位模式是一样的. C语言可以保证-x=~x+1. 同样也分两种情况讨论.见代码.
[代码]
1 /* Determine whether arguments can be subtracted without overflow */ 2 3 int tsub_ok(int x, int y) 4 5 { 6 7 #if 0 8 9 if (y == INT_MIN) 10 11 return x<0; 12 13 else 14 15 return tadd_ok(x, -y); 16 17 #endif 18 19 return y==INT_MIN&&x<0 || y!=INT_MIN&&tadd_ok(x, -y); 20 21 }
☞问题六: 有符号数的乘法越界问题
[定理]
完全同无符号的乘法一样.
[代码]
1 /* Determine whether arguments can be multiplied without overflow. */ 2 3 int tmul_ok(int x, int y) 4 5 { 6 7 #if 0 8 9 int p = x * y; 10 11 return !x || p/x==y; 12 13 #endif 14 15 return umul_ok(x, y); /* 直接调用 */ 16 17 }




