20192317邓子彦 实验九 《数据结构与面向对象程序设计》实验报告
20192317邓子彦 实验九 《数据结构与面向对象程序设计》实验报告
课程:《程序设计与数据结构》
班级: 1923
姓名: 邓子彦
学号:20192317
实验教师:王志强
实验日期:2020年12月27日
必修/选修: 必修
1. 实验内容
- (1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
- (2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
- (3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
- (4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
- (5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
PS:本题12分。目前没有明确指明图的顶点和连通边,如果雷同或抄袭,本次实验0分。
2. 实验过程及结果
提交点一
- 实验代码
//图类
import java.util.Scanner;
public class Graph {
/**
* 图的节点个数
*/
int verNum;
/**
* 图的边的条数
*/
int edgeNum;
/**
* 图的邻接表中存储节点的数组
*/
Vertex[] verArray;
/**
* Graph类的构造方法,依次读取节点、边等信息,完成图的构建。
*/
public Graph() {
Scanner scan = new Scanner(System.in);
System.out.println("构建有向图输入0,构建无向图输入1 ");
int choose = scan.nextInt();
System.out.println("节点个数和边个数:");
verNum = scan.nextInt();
edgeNum = scan.nextInt();
verArray = new Vertex[verNum];
System.out.println("依次输入节点名称:");
for (int i=0;i<verNum;i++){
Vertex vertexmem = new Vertex();
vertexmem.verName = scan.next();
vertexmem.edgeLink = null;
verArray[i] = vertexmem;
}
System.out.println("请按‘头节点 尾节点 回车’的形式依次输入边的信息");
for (int i=0;i<edgeNum;i++){
String preName = scan.next();
String folName = scan.next();
Vertex preV = getVertex(preName);
Vertex folV = getVertex(folName);
if (preV == null || folV == null){
System.out.println("输入错误,输入了不存在的顶点!请重新输入");
i--;
continue;
}
Edge edge = new Edge();
edge.tailName = folName;
//将边加入到节点的链表中去
edge.broEdge = preV.edgeLink;//循环
preV.edgeLink = edge;//放在出始地的后面
//如果加上下面这段,则创建的是无向图,不加则是有向图
if(choose==1){
//edge.tailName = preName;
//edge.broEdge = folV.edgeLink;
//folV.edgeLink = edge;
Edge edgeelse = new Edge();
edgeelse.tailName = preName;
edgeelse.broEdge = folV.edgeLink;
folV.edgeLink = edgeelse;
}
}
}
public Vertex getVertex(String verName){
for (int i=0;i<verNum;i++){
if (verArray[i].verName.equals(verName))
return verArray[i];
}
return null;
}
}
//GraphTest
import java.util.Stack;
public class Test {
public static void main(String[] args) {
Graph graph = new Graph();
System.out.println("该图的邻接表为:");
outputGraph(graph);
}
/**
* 输出图的邻接表的方法。
* @param graph 要输出的图
*/
public static void outputGraph(Graph graph){
for (int i=0;i<graph.verNum;i++){
Vertex vertex = graph.verArray[i];
System.out.print(vertex.verName);
Edge current = vertex.edgeLink;
while (current != null){
System.out.print("-->"+current.tailName);
current = current.broEdge;
}
System.out.println();
}
}
public static void outputtuota(Graph graph,int[] a){
Stack<Integer> stack = new Stack<>();
for (int i=0;i<graph.verNum;i++){
if(a[i]==0){
System.out.println(i+1);
}
}
}
}
- 实验截图
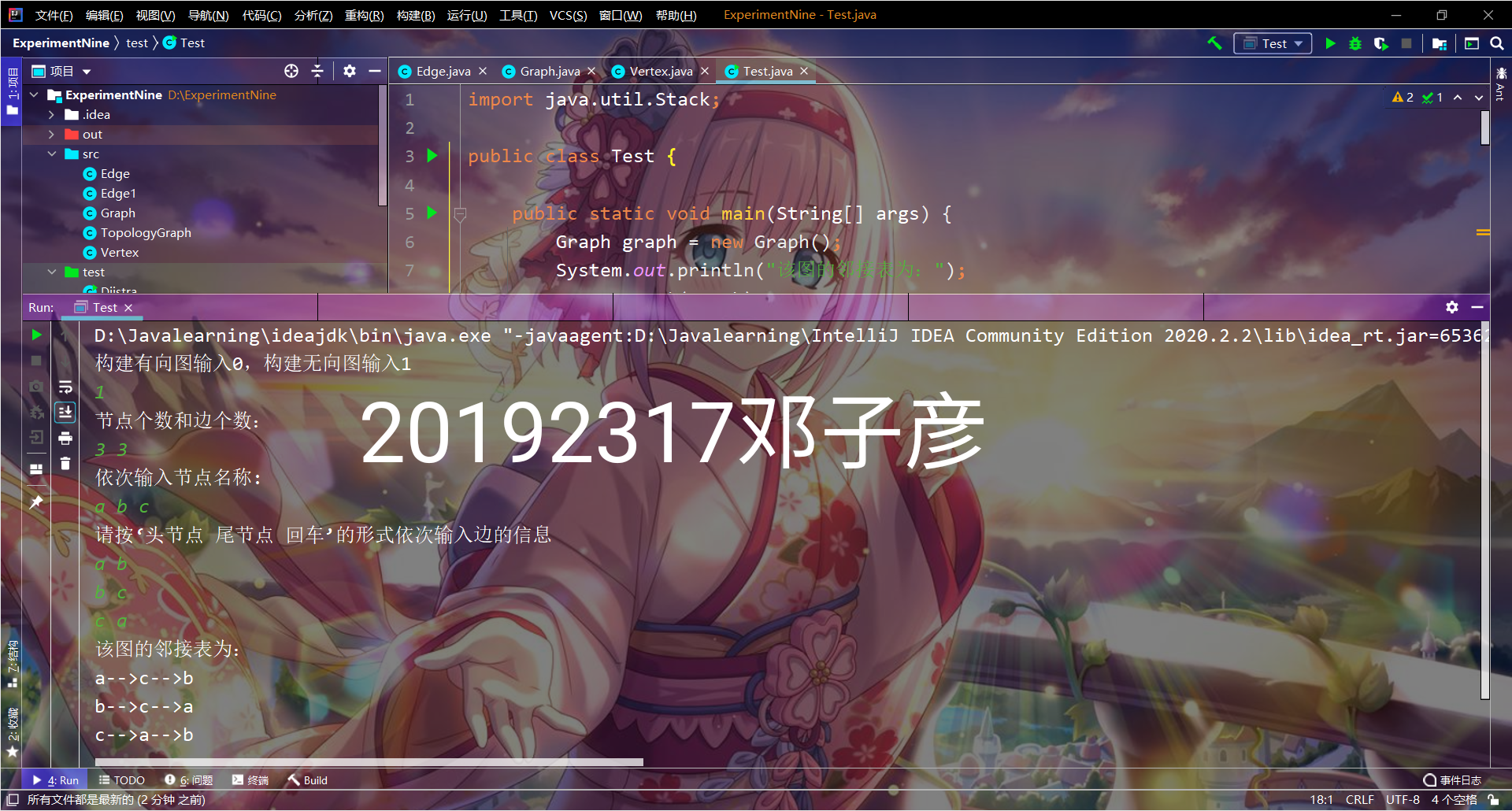
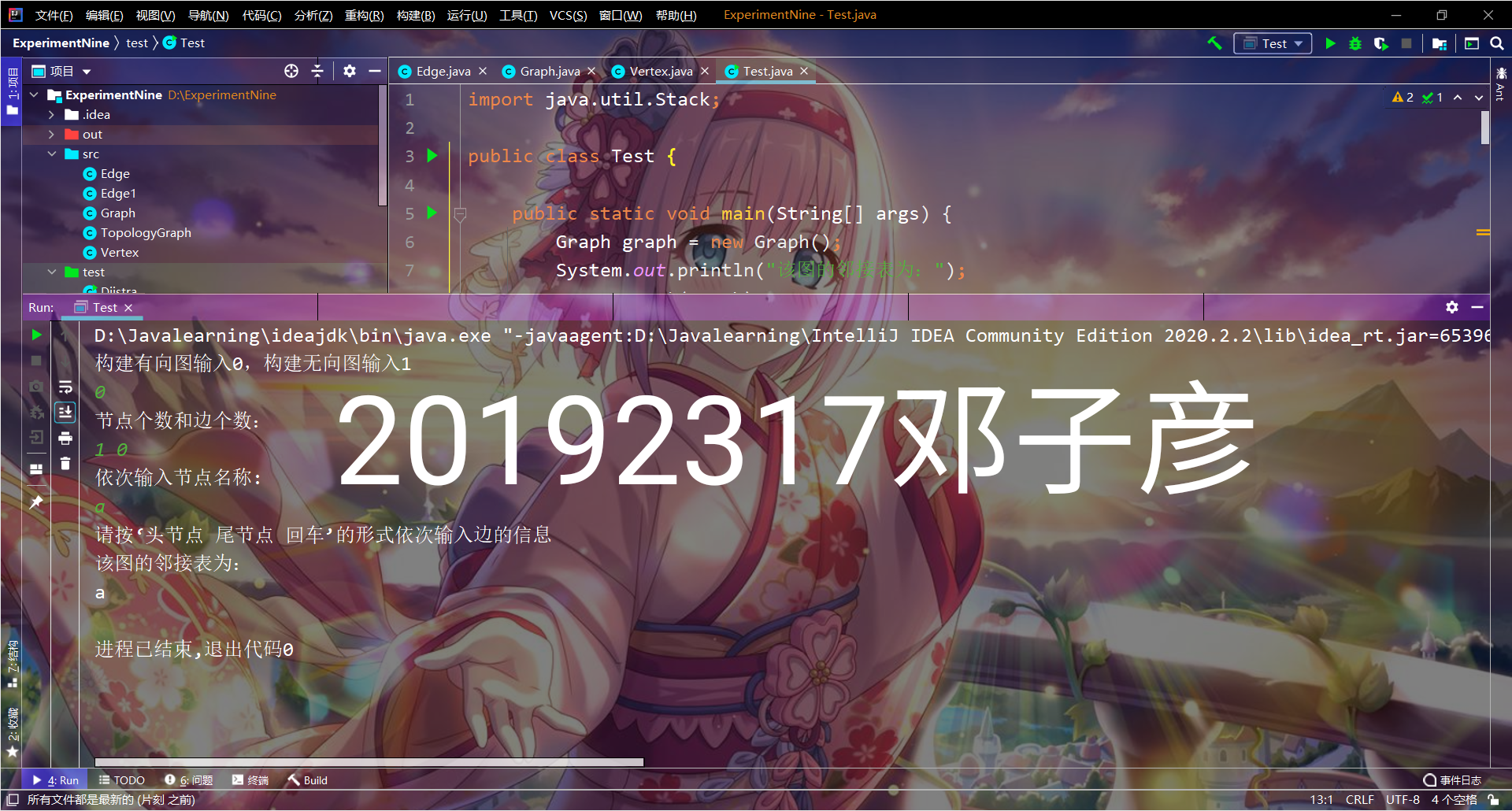
提交点二
- 实验代码
//图的遍历,深度和广度优先遍历
import java.util.*;
/**
* 使用java实现图的图的广度优先 和深度优先遍历算法。
*/
public class GraphTraversalTest {
private Map<String, List<String>> graph = new HashMap<String, List<String>>();
/**
* 初始化图数据:使用邻居表来表示图数据。
*/
public void initGraphData() {
graph.put("1", Arrays.asList("2", "3"));
graph.put("2", Arrays.asList("1", "4", "5"));
graph.put("3", Arrays.asList("1", "6", "7"));
graph.put("4", Arrays.asList("2", "8"));
graph.put("5", Arrays.asList("2", "8"));
graph.put("6", Arrays.asList("3", "8", "9"));
graph.put("7", Arrays.asList("3", "9"));
graph.put("8", Arrays.asList("4", "5", "6"));
graph.put("9", Arrays.asList("6", "7"));
}
/**
* 宽度优先搜索(BFS, Breadth First Search)
* BFS使用队列(queue)来实施算法过程
*/
private Queue<String> queue = new LinkedList<String>();
private Map<String, Boolean> status = new HashMap<String, Boolean>();
/**
* 开始点
*
* @param startPoint
*/
public void BFSSearch(String startPoint) {
//1.把起始点放入queue;
queue.add(startPoint);
status.put(startPoint, false);
bfsLoop();
}
private void bfsLoop() {
// 1) 从queue中取出队列头的点;更新状态为已经遍历。
String currentQueueHeader = queue.poll(); //出队
status.put(currentQueueHeader, true);
System.out.println(currentQueueHeader);
// 2) 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入queue中。
List<String> neighborPoints = graph.get(currentQueueHeader);
for (String poinit : neighborPoints) {
if (!status.getOrDefault(poinit, false)) { //未被遍历
if (queue.contains(poinit)) continue;
queue.add(poinit);
status.put(poinit, false);
}
}
if (!queue.isEmpty()) { //如果队列不为空继续遍历
bfsLoop();
}
}
private Stack<String> stack = new Stack<String>();
public void DFSSearch(String startPoint) {
stack.push(startPoint);
status.put(startPoint, true);
dfsLoop();
}
private void dfsLoop() {
if(stack.empty()){
return;
}
//查看栈顶元素,但并不出栈
String stackTopPoint = stack.peek();
// 2) 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入queue中。
List<String> neighborPoints = graph.get(stackTopPoint);
for (String point : neighborPoints) {
if (!status.getOrDefault(point, false)) { //未被遍历
stack.push(point);
status.put(point, true);
dfsLoop();
}
}
String popPoint = stack.pop();
System.out.println(popPoint);
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
System.out.println("选择深度遍历输入1,广度遍历输入0");
int choose = scan.nextInt();
GraphTraversalTest test = new GraphTraversalTest();
test.initGraphData();
if(choose==0){
System.out.println("广度优先遍历 :");
test.BFSSearch("1");}
if(choose==1){
System.out.println("深度优先遍历: ");
test.DFSSearch("1");}
}
}
- 实验截图
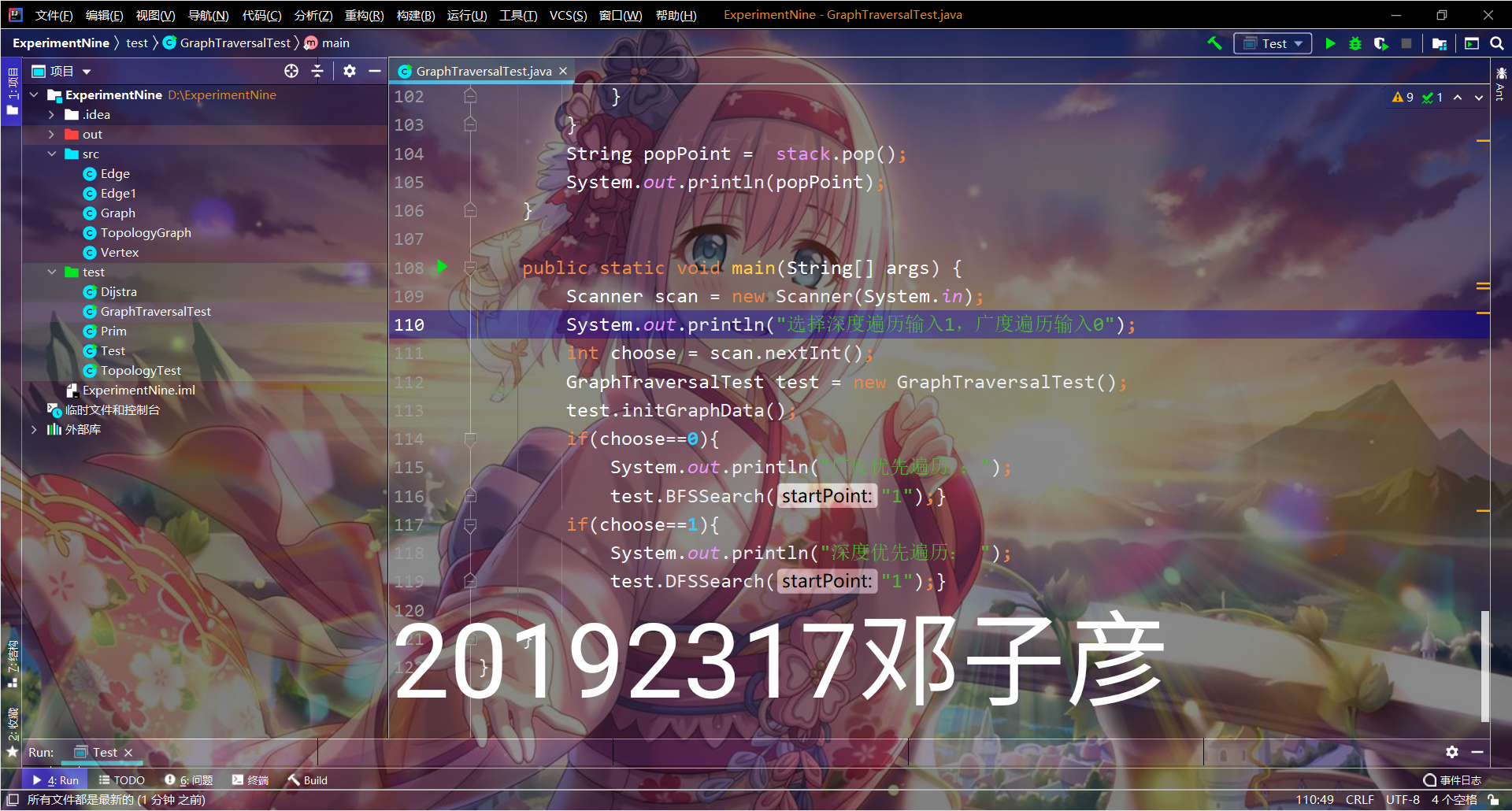
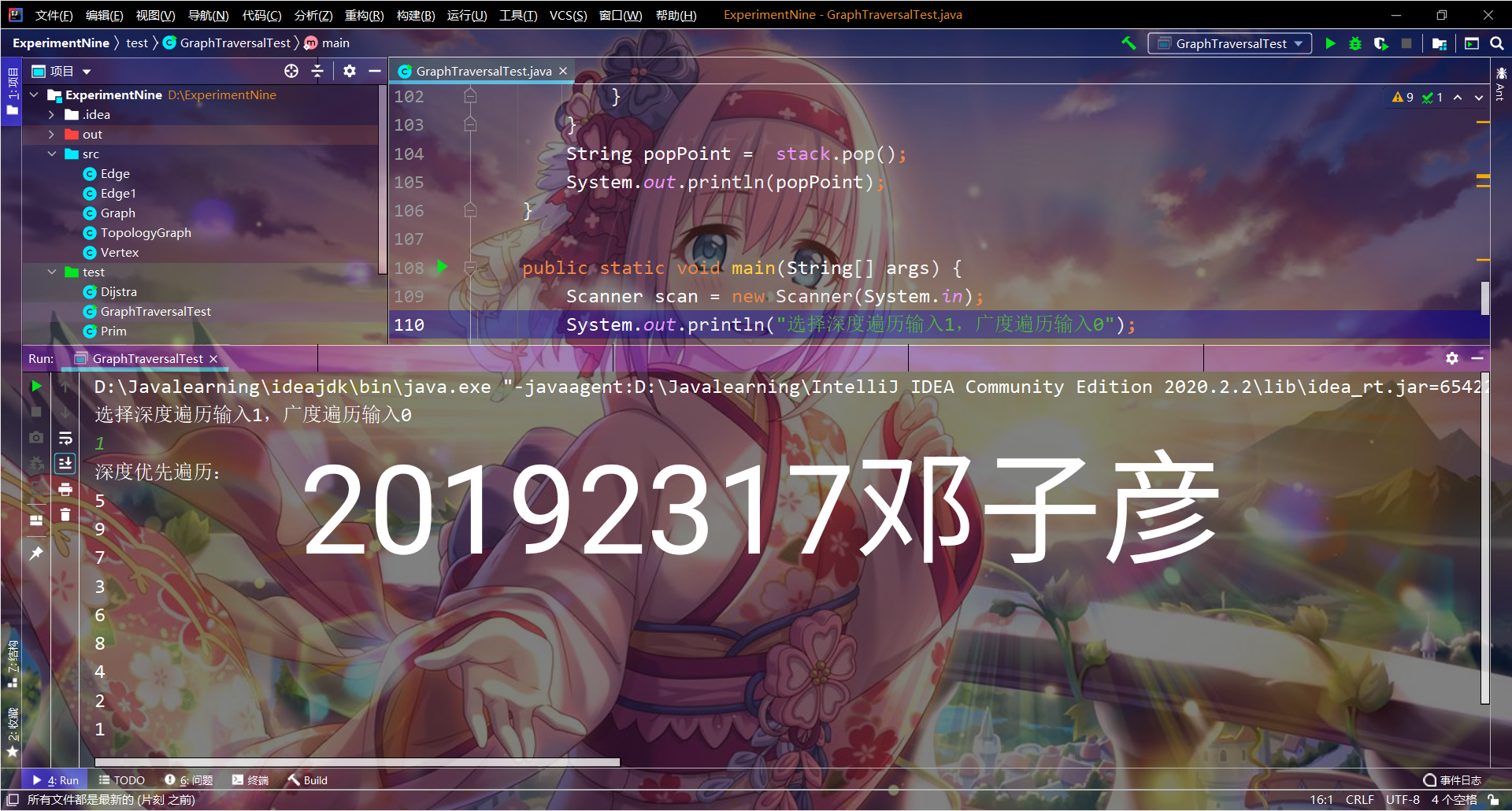
提交点三
- 实验代码
//拓扑
import java.io.*;
public class TopologyTest {
public static void main(String[] args) throws IOException {
TopologyGraph directedGraph = new TopologyGraph();
try{
directedGraph.topoSort();
}catch(Exception e){
System.out.println("graph has circle");
e.printStackTrace();
}
}
}
- 实验截图
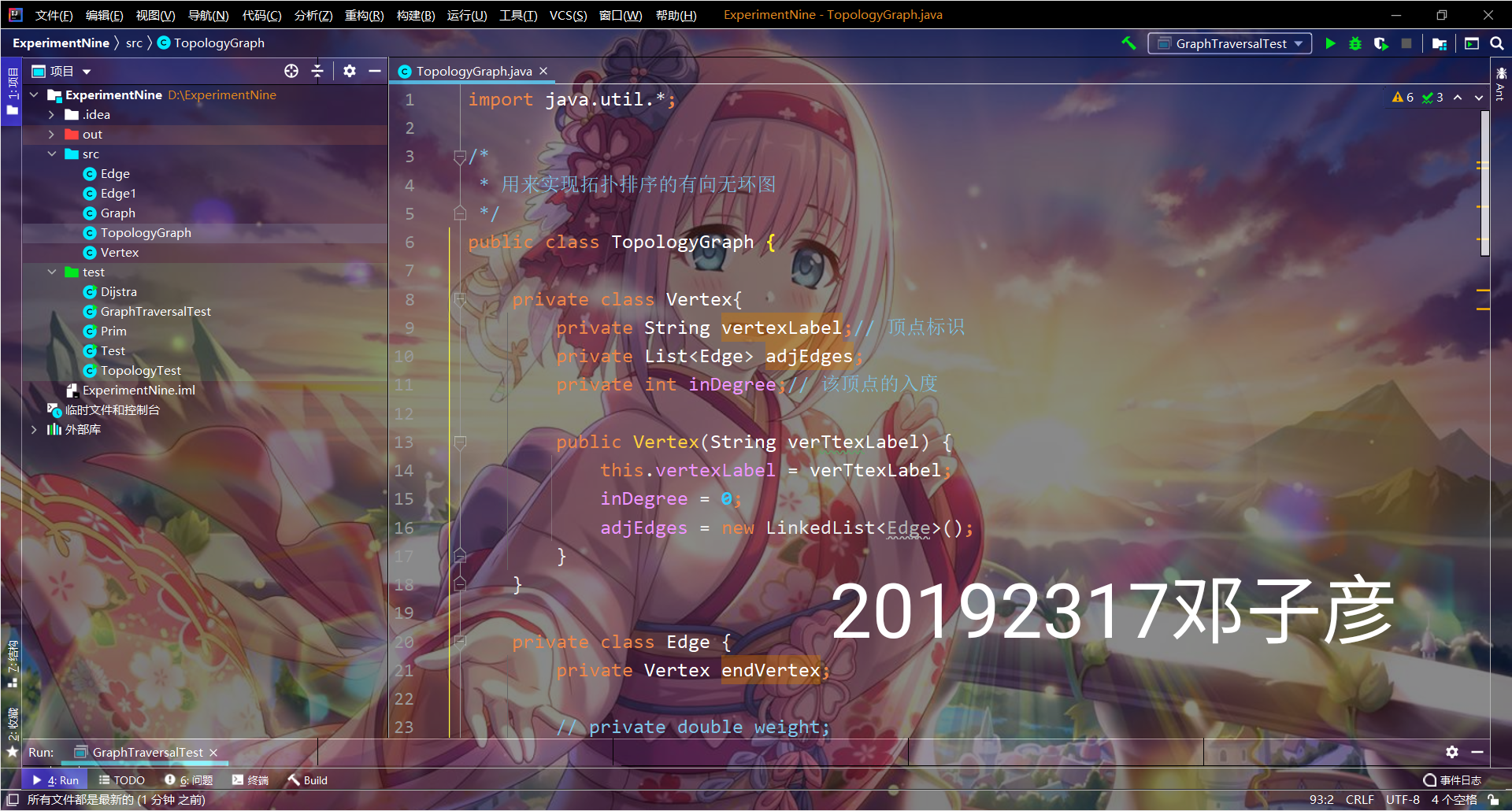
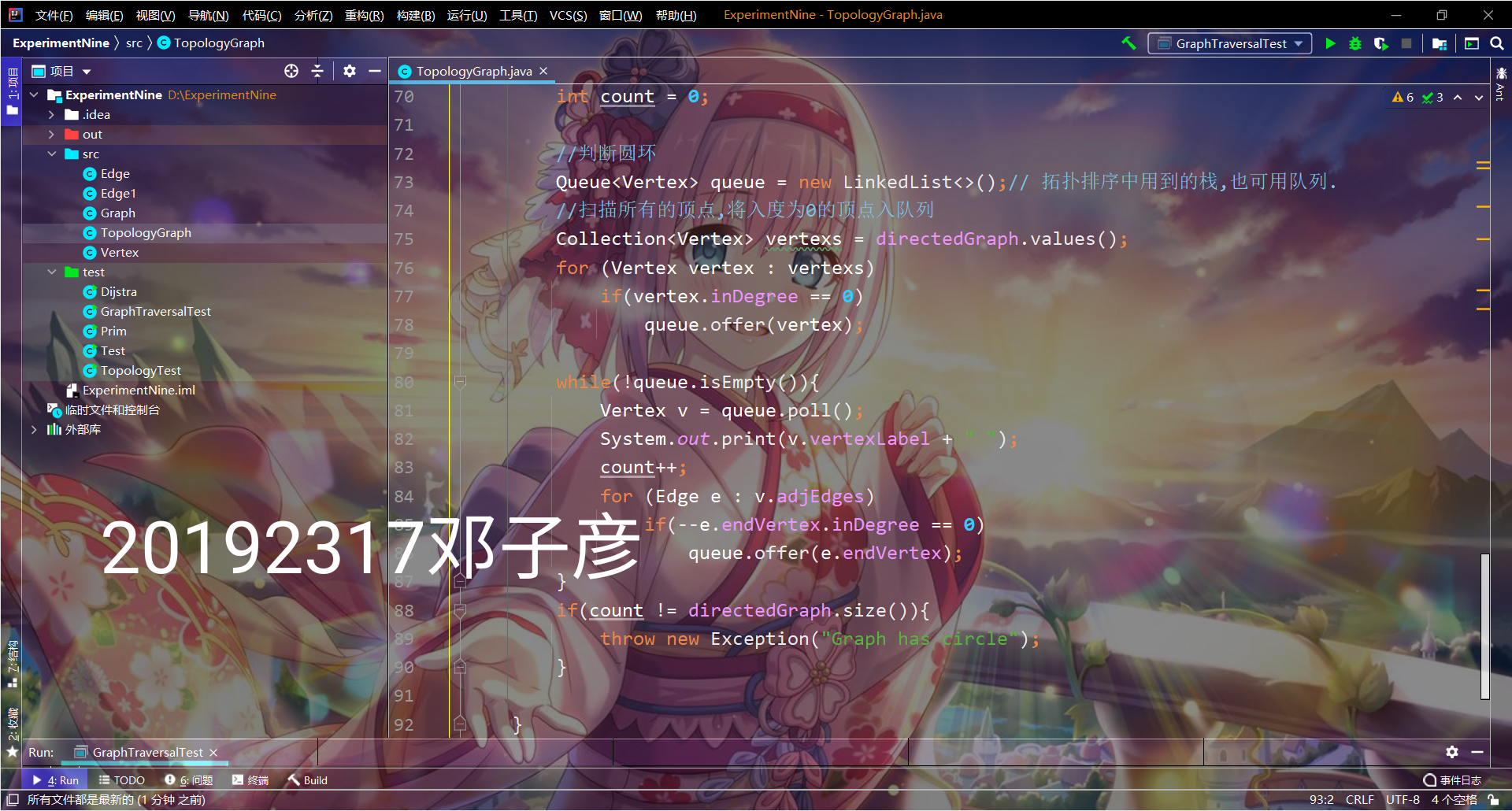
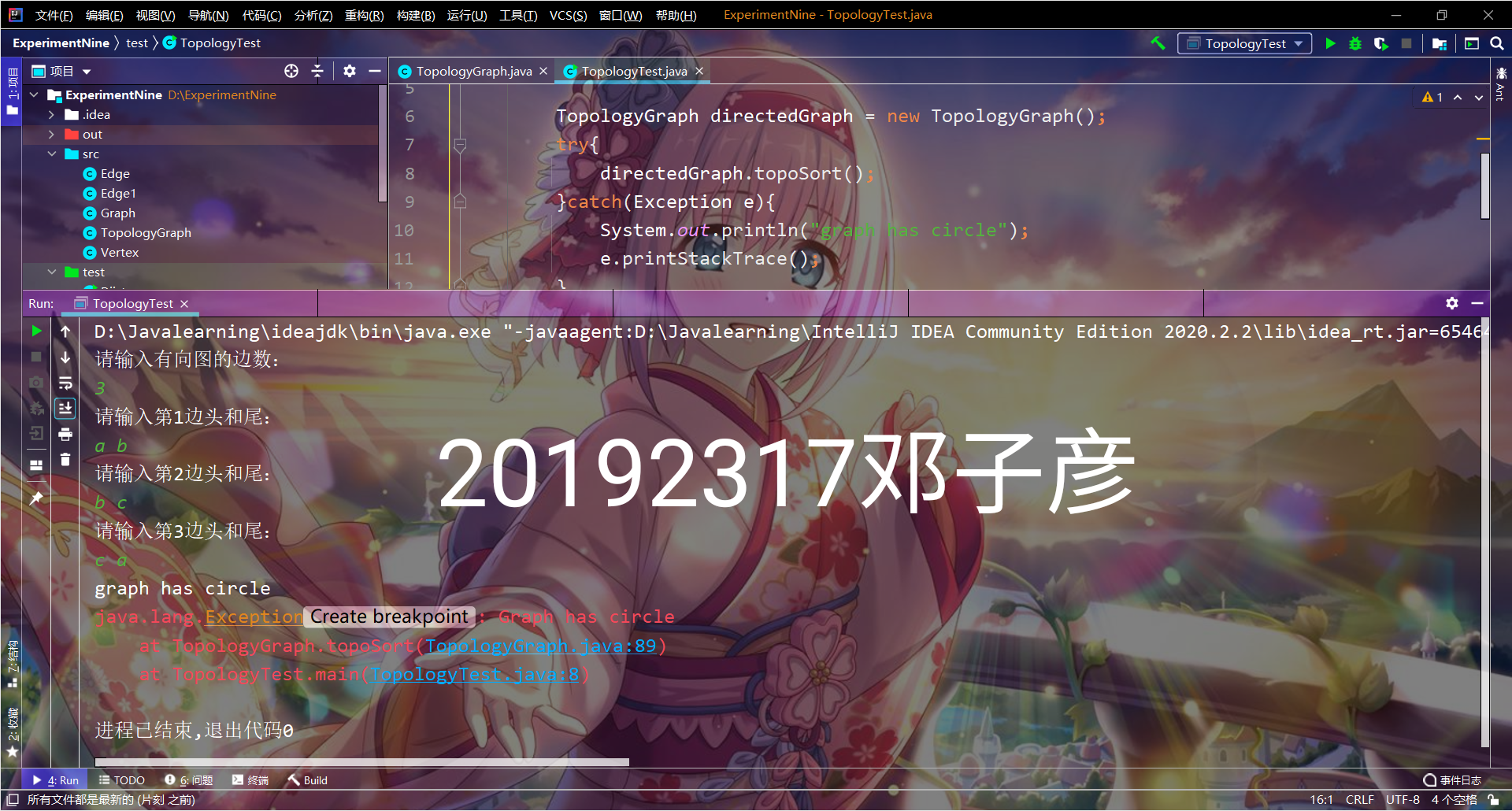
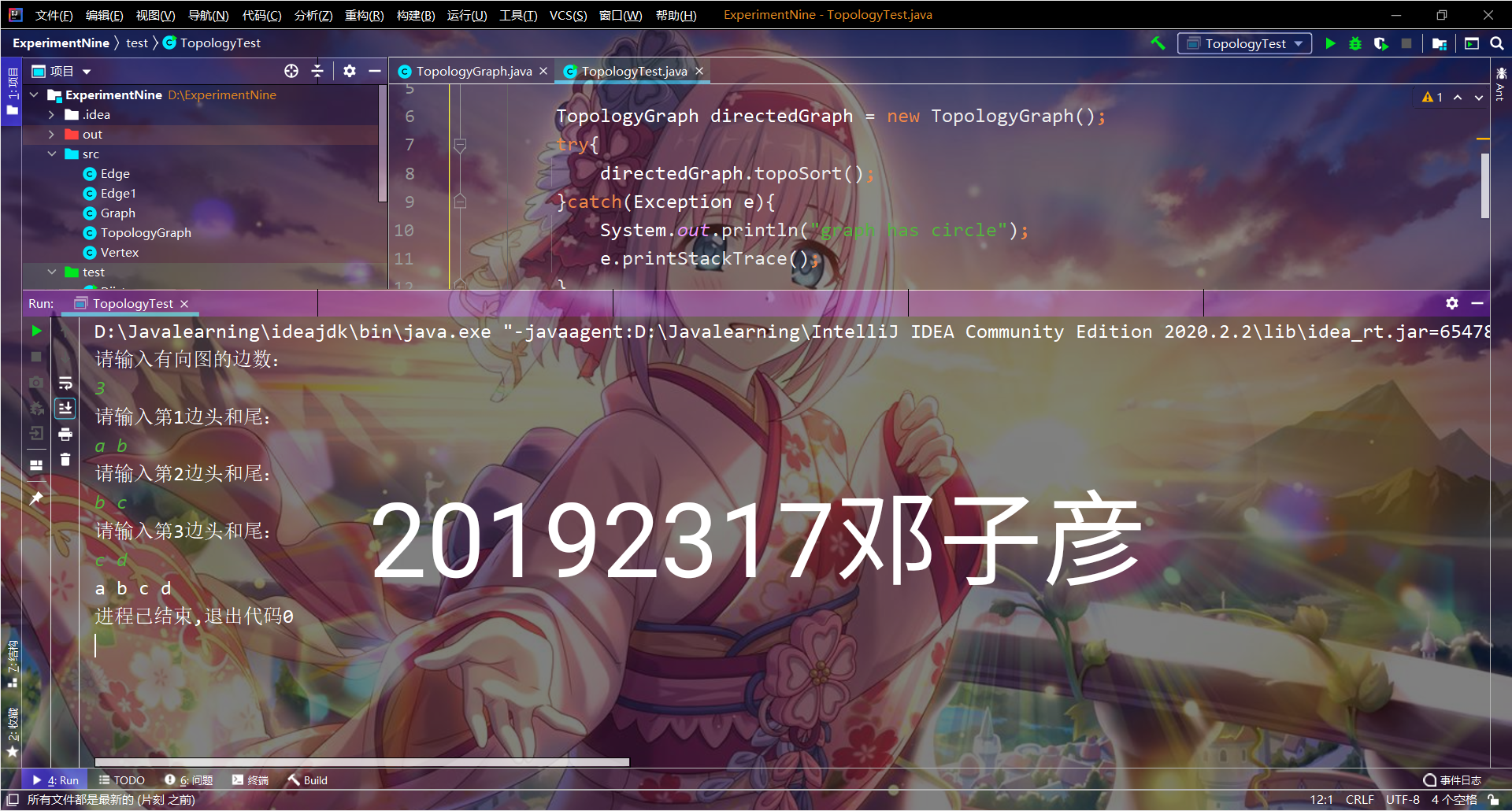
提交点四
- 实验代码
//Prim算法
public class Prim {
public static void PRIM(int [][] graph,int start,int n){
int [][] mins=new int [n][2];//用于保存集合U到V-U之间的最小边和它的值,mins[i][0]值表示到该节点i边的起始节点
//值为-1表示没有到它的起始点,mins[i][1]值表示到该边的最小值,
//mins[i][1]=0表示该节点已将在集合U中
for(int i=0;i<n;i++){//初始化mins
if(i==start){
mins[i][0]=-1;
mins[i][1]=0;
}else if( graph[start][i]!=-1){//说明存在(start,i)的边
mins[i][0]=start;
mins[i][1]= graph[start][i];
}else{
mins[i][0]=-1;
mins[i][1]=Integer.MAX_VALUE;
}
// System.out.println("mins["+i+"][0]="+mins[i][0]+"||mins["+i+"][1]="+mins[i][1]);
}
for(int i=0;i<n-1;i++){
int minV=-1,minW=Integer.MAX_VALUE;
for(int j=0;j<n;j++){//找到mins中最小值,使用O(n^2)时间
if(mins[j][1]!=0&&minW>mins[j][1]){
minW=mins[j][1];
minV=j;
}
}
// System.out.println("minV="+minV);
mins[minV][1]=0;
System.out.println("最小生成树的第"+i+"条最小边=("+(mins[minV][0]+1)+","+(minV+1)+"),权重="+minW);
for(int j=0;j<n;j++){//更新mins数组
if(mins[j][1]!=0){
// System.out.println("MINV="+minV+"||tree[minV][j]="+tree[minV][j]);
if( graph[minV][j]!=-1&& graph[minV][j]<mins[j][1]){
mins[j][0]=minV;
mins[j][1]= graph[minV][j];
}
}
}
}
}
}
- 实验截图
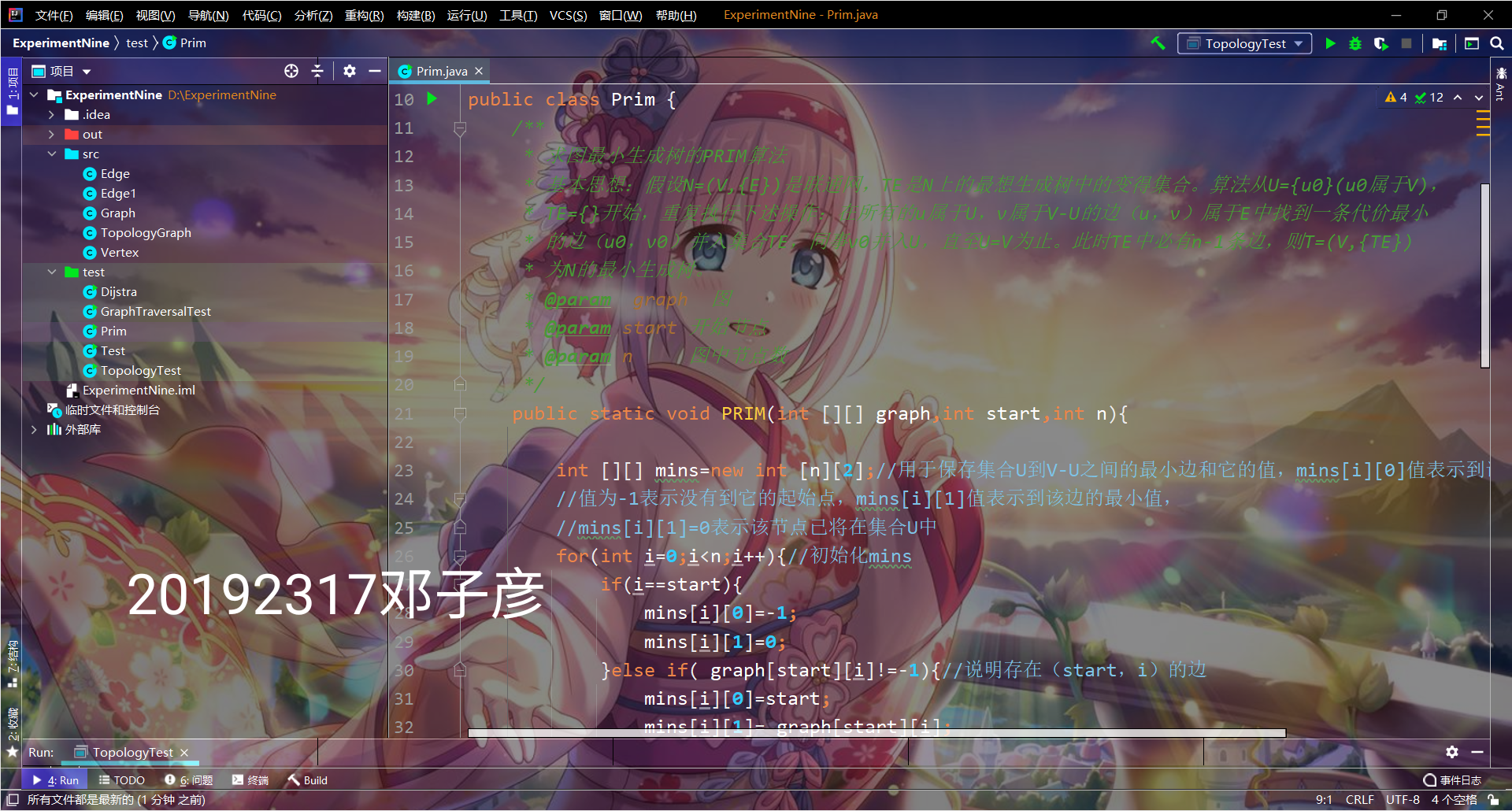
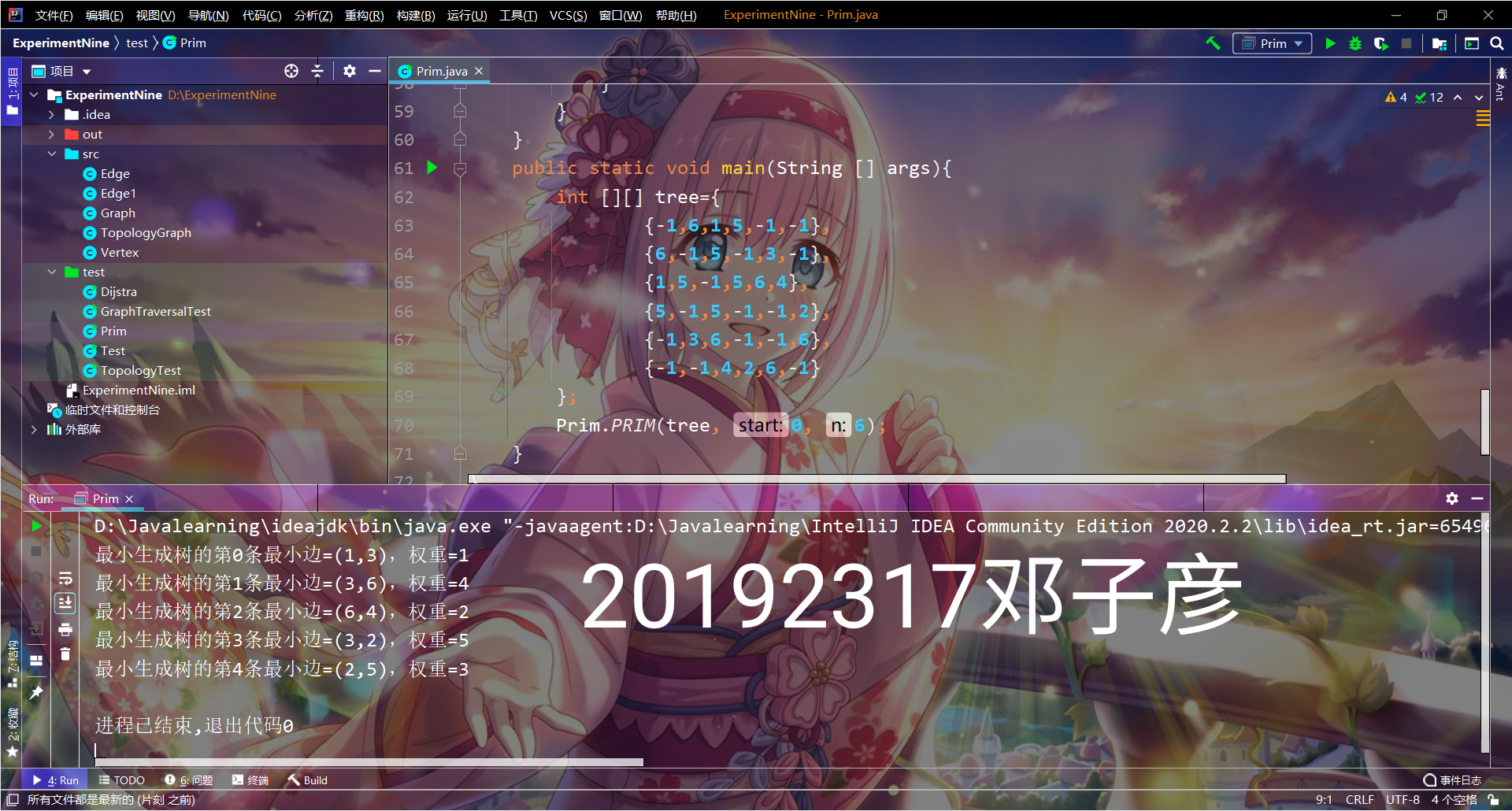
提交点五
- 实验代码
//通过迪杰斯特拉算法完成有向图的单源最短路径求解
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
import java.util.Stack;
public class Dijstra {
public static void main(String[] args) {
int vertexNum = 5;
char[] vertexs = new char[] { 'A', 'B', 'C', 'D', 'E' };
int[][] matrix = new int[][] { { 0, 10, Integer.MAX_VALUE / 2, Integer.MAX_VALUE / 2, 5 },
{ Integer.MAX_VALUE / 2, 0, 1, Integer.MAX_VALUE / 2, 2 },
{ Integer.MAX_VALUE / 2, Integer.MAX_VALUE / 2, 0, 4, Integer.MAX_VALUE / 2 },
{ 7, Integer.MAX_VALUE / 2, 6, 0, Integer.MAX_VALUE / 2 },
{ Integer.MAX_VALUE / 2, 3, 9, 2, 0 } }; // matrix[i][j]为0表示i==j,matrix[i][j]为Integer.MAX_VALUE/2表示两个顶点不是图的边,否则表示边的权值
Graph g = new Graph(vertexNum, vertexs, matrix);
Scanner sc = new Scanner(System.in);
int srcIndex;
do{
System.out.print("请输入源点索引(0~4):");
srcIndex = sc.nextInt();
}while(srcIndex < 0 || srcIndex > 4);
System.out.println(g.vertexs[srcIndex] + "作为源点");
Info info = dijkstra(g, srcIndex); // 指定将索引为srcIndex的顶点作为源点
for(int i : info.pathSerials){
System.out.print(g.vertexs[i] + " ");
}
System.out.println();
int index = 0;
for(int[] path : info.paths){
for(int i : path){
System.out.print(g.vertexs[i]);
}
System.out.println(": " + info.distances[index++]);
}
sc.close();
}
// 通过迪杰斯特拉(Dijkstra)算法求以vertex[srcIndex]顶点作为源点到其余各顶点的最短路径
public static Info dijkstra(Graph g, int srcIndex) {
if(srcIndex < 0 || srcIndex >= g.vertexNum){
return null;
}
int[] pathSerials = new int[g.vertexNum]; // pathSerials[i]表示从源点到顶点i的最短路径(即若P(srcIndex,j)={V(srcIndex)...Vk...Vs...Vj}是从源点srcIndex到j的最短路径,则有P(srcIndex,j)=P(srcIndex,k)+P(k,s)+P(s,j))
int[] path = new int[g.vertexNum]; // path[i]表示从源点到顶点i(i为vertexs中的索引)的最短路径中顶点i的前驱顶点
int index = 0;
pathSerials[index] = srcIndex; // 源点加入序列中
g.visited[srcIndex] = true; // 源点已在最短路径序列中
Arrays.fill(path, -1); // -1表示顶点没有前驱顶点
int[] distances = new int[g.vertexNum]; // distances[i]表示从源点到顶点i(i为vertexs中的索引)的当前最短路径长度
for (int i = 0; i < g.vertexNum; i++) {
// 初始化distances为其余顶点到源点的权值
distances[i] = g.matrix[srcIndex][i];
}
int minIndex = srcIndex;
while (minIndex != -1) { // 仍有未加入到最短路径序列中的顶点
index++;
for (int i = 0; i < g.vertexNum; i++) {
if (!g.visited[i]) { // 更新仍未加入到最短路径序列中的顶点的从源点到它的值
// 这些仍未加入到最短路径序列中的顶点的distances[i]值为(刚加入的顶点minIndex的distances[minIndex]与minIndex到顶点i之和)与(顶点minIndex刚加入之前源点到i的距离值distances[i])两者之间的较小者
distances[i] = Math.min(distances[i], distances[minIndex] + g.matrix[minIndex][i]);
// 如果当前顶点i的distances[i]值为新加入的顶点minIndex,则顶点i的前驱为minIndex,否则不变
if(distances[i] == distances[minIndex] + g.matrix[minIndex][i] && distances[i] != Integer.MAX_VALUE / 2){ // distances[i] != Integer.MAX_VALUE / 2表示仍不可达,就没有前驱
path[i] = minIndex;
}
}
}
minIndex = indexOf(g, distances); // 选出的最小顶点
if(minIndex == -1){
break;
}
pathSerials[index] = minIndex; // 刚选出的最小顶点加入到最短路径序列中
g.visited[minIndex] = true;
}
return new Info(distances, pathSerials, getPathOfAll(path, pathSerials));
}
// 找到图中仍未加入到最短路径序列顶点集中到源点距离最小的顶点的索引
public static int indexOf(Graph g, int[] distances) {
int min = Integer.MAX_VALUE / 3;
int minIndex = -1; // 当前数组distances剩余元素最小值(-1表示无剩余元素)--剩余元素就是仍未加入到最短路径序列中的顶点
for(int i = 0; i < g.vertexNum; i++){
if(!g.visited[i]){ // 如果i顶点仍未加入到最短路径序列中
if(distances[i] < min){
min = distances[i];
minIndex = i;
}
}
}
return minIndex;
}
// 得到指定顶点i的从源点到顶点i的最短路径(均以顶点集vertexs中索引表示)
public static int[] getPath(int[] path, int i){
Stack<Integer> s = new Stack<Integer>();
s.push(i);
int pre = path[i];
while(pre != -1){
s.push(pre);
pre = path[pre];
}
int size = s.size();
int[] pathOfVertex = new int[size];
while(!s.isEmpty()){
pathOfVertex[size - s.size()] = s.pop();
}
return pathOfVertex;
}
public static ArrayList<int[]> getPathOfAll(int[] path, int[] pathSerials){
ArrayList<int[]> paths = new ArrayList<int[]>();
for(int i = 0; i < pathSerials.length; i++){
paths.add(getPath(path, i));
}
return paths;
}
public static class Graph{
private int vertexNum;
private char[] vertexs;
private int[][] matrix;
private boolean visited[];
public Graph(int vertexNum, char[] vertexs, int[][] matrix){
this.vertexNum = vertexNum;
this.vertexs = vertexs;
this.matrix = matrix;
visited = new boolean[vertexNum];
}
}
public static class Info{
private int[] distances; // 源点到各个顶点的最短距离
private int[] pathSerials; // 整个最短路径序列
private ArrayList<int[]> paths; // 源点到各个顶点的确切最短路径序列
public Info(int[] distances, int[] pathSerials, ArrayList<int[]> paths) {
this.distances = distances;
this.pathSerials = pathSerials;
this.paths = paths;
}
}
}
- 实验截图



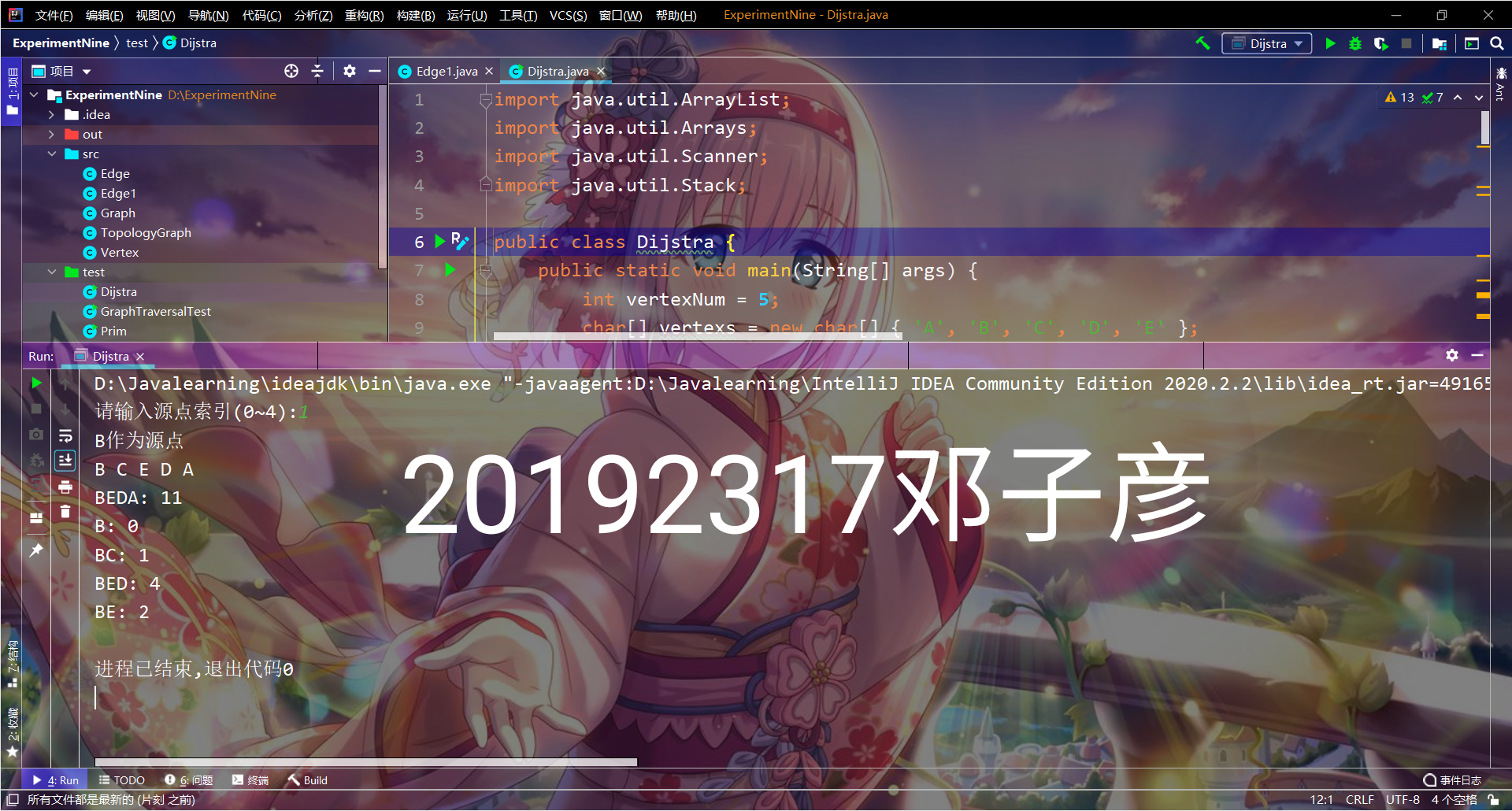

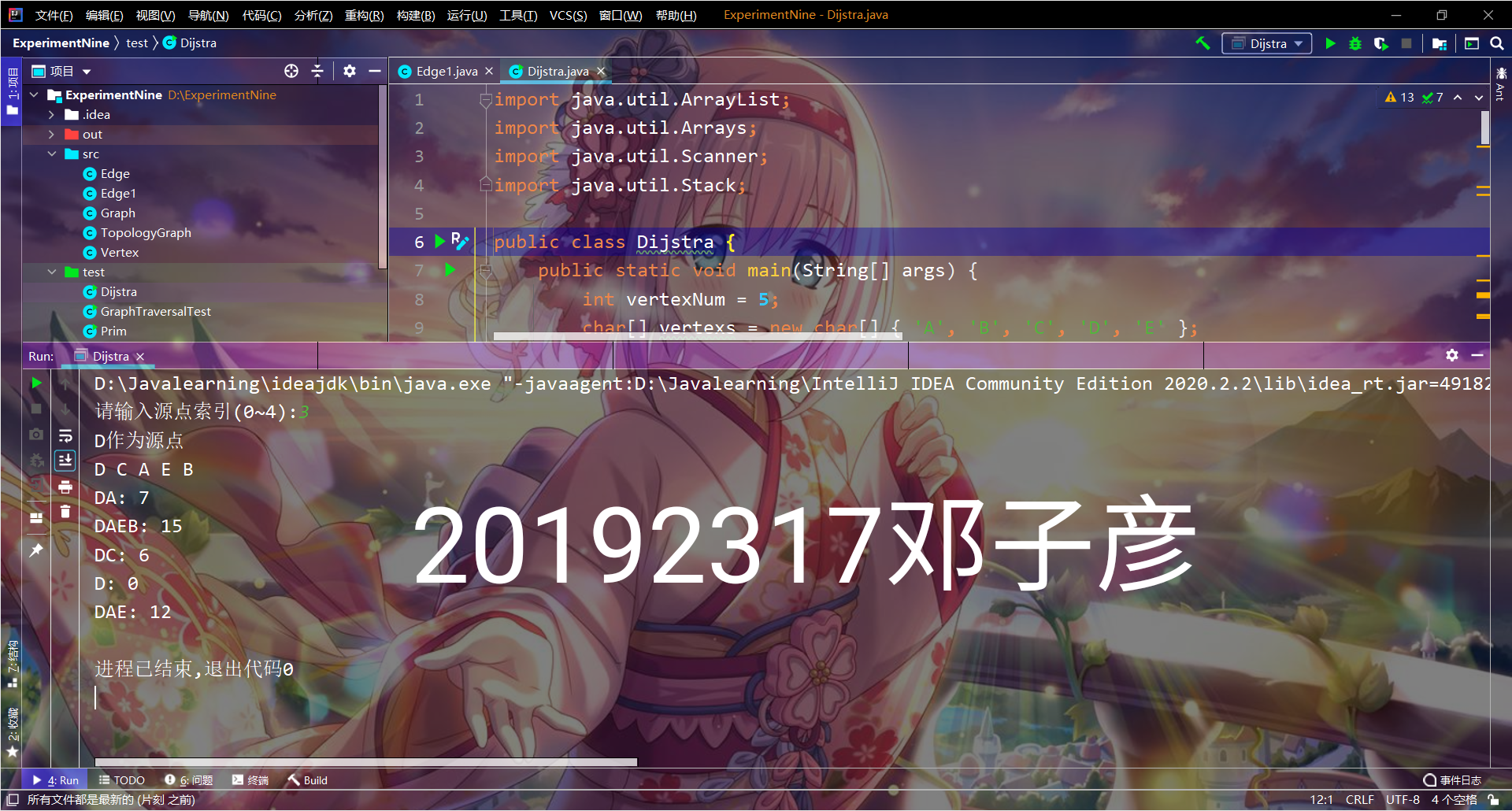
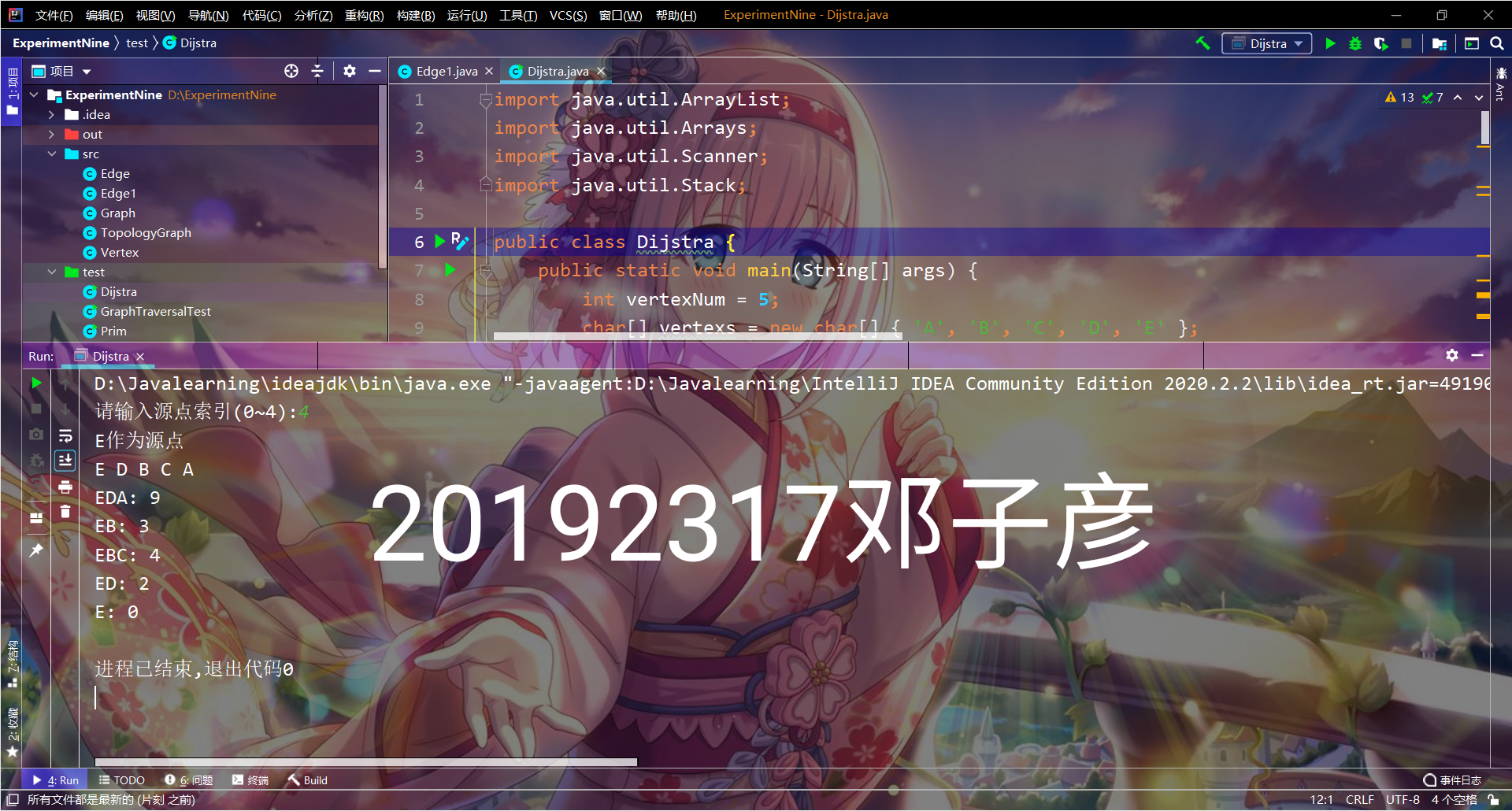
3. 心得体会
- 这次图的实验非常难,可能后面赶课时导致老师没有时间带我们进行代码的实践,所以这个实验操作起来十分困难,通过问同学和上CSDN学习图的知识完成了这次实验。



