插值
在一段连续的函数中,插入指定n个点, 填满空隙
一维插值
import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
import pylab as pl
x = np.linspace(0,10,11)
y = np.sin(x)
x_new = np.linspace(0,10,101)
pl.plot(x,y,'ro')
for kind in ['nearest','zero','slinear','quadratic','cubic']:
f = interpolate.interp1d(x,y,kind=kind)
y_new = f(x_new)
pl.plot(x_new,y_new,label=str(kind))
pl.legend(loc='lower right')
plt.savefig(u'./一维插值.png')

二维插值
import numpy as np
from scipy import interpolate
import pylab as pl
import matplotlib as mpl
def func(x,y):
'''
x 的2次幂
y 的2次幂
'''
return (x+y)*np.exp(-5.0*(x**2+y**2))
y,x = np.mgrid[-1:1:15j,-1:1:15j]
fvals = func(x,y)
print len(fvals[0])
new_func = interpolate.interp2d(x,y,fvals,kind='cubic')
x_new = np.linspace(-1,1,100)
y_new = np.linspace(-1,1,100)
f_new = new_func(x_new,y_new)
pl.subplot(121)
im1 = pl.imshow(fvals,extent=[-1,1,-1,1],cmap=mpl.cm.hot,interpolation='nearest',origin='lower')
pl.colorbar(im1)
pl.subplot(122)
im2 = pl.imshow(f_new,extent=[-1,1,-1,1],cmap=mpl.cm.hot,interpolation='nearest',origin='lower')
pl.colorbar(im2)
pl.savefig(u'./二维插值')
pl.show()

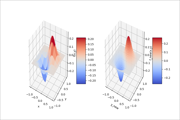
二维插值的三维展示方法
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt
def func(x, y):
return (x + y) * np.exp(-5 * (x ** 2 + y ** 2))
x = np.linspace(-1, 1, 20)
y = np.linspace(-1, 1, 20)
x, y = np.meshgrid(x, y)
fvals = func(x, y)
fig = plt.figure(figsize=(9, 6))
ax = plt.subplot(1, 2, 1, projection='3d')
surf = ax.plot_surface(x, y, fvals, rstride=2, cstride=2, cmap=cm.coolwarm, linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
plt.colorbar(surf, shrink=0.5, aspect=5)
new_func = interpolate.interp2d(x, y, fvals, kind='cubic')
x_new = np.linspace(-1, 1, 100)
y_new = np.linspace(-1, 1, 100)
f_new = new_func(x_new, y_new)
x_new, y_new = np.meshgrid(x_new, y_new)
ax2 = plt.subplot(1, 2, 2, projection='3d')
surf2 = ax2.plot_surface(x_new, y_new, f_new, rstride=2, cstride=2, cmap=cm.coolwarm, linewidth=0.5, antialiased=True)
ax2.set_xlabel('x_new')
ax2.set_xlabel('y_new')
ax2.set_zlabel('f_new(x,y)')
plt.colorbar(surf2, shrink=0.5, aspect=5)
plt.show()








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!
· AI与.NET技术实操系列(二):开始使用ML.NET
· 单线程的Redis速度为什么快?