最长单调递增子序列LIS（《算法导论》15.4-5题）

LIS问题可以转化为LCS问题求解，或者转化为动态规划方式求解。

LCS问题的递推式为：

                           

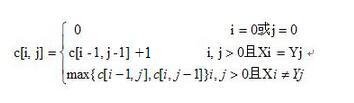
动态规划法递推式为：

                          

 

LCS程序上一篇文章里有写过，这里是第二种方法的程序（参考了《算法导论》及其他人的程序）：

import java.util.Scanner;

public class LIS {
    public static void main(String[] args) {
        //从控制台获取输入，并转换为整型数组（以空格作为分隔符，输入整数）
        Scanner sc=new Scanner(System.in);
        String[] s=sc.nextLine().split(" ");
        int[] arr=new int[s.length];
        for(int i=0;i<s.length;i++){
            arr[i]=Integer.parseInt(s[i]);
        }
        /*for(int x:arr){//for each用法
            System.out.print(x+" ");
        }*/ 
        
        //动态规划法（f(i)表示arr中以ai为末元素的最长递增子序列的长度）
        int n=arr.length;
        int[] f=new int[n];          //用于存放f(i)值
        f[0]=1;                      //以第a1为末元素的最长递增子序列长度为1
        for(int i=1;i<n;i++){        //循环n-1次
            f[i]=1;                  //f[i]的最小值为1
            for(int j=0;j<i;j++){    //循环i次
                if(arr[j]<arr[i]&&f[j]+1>f[i]){
                    f[i]=f[j]+1;     //更新f[i]的值
                }
            }
        }
        System.out.println(f[n-1]);
        sc.close();
    }
}