JavaSE—二维数组
二维数组
有些时候数据并不是线性的，而是区分行和列的，像围棋盘，当你要保存数据的时候，就需要按照行和列标准的去保存数据，这个时候用一维的数组就不方便了，所以这个时候就可以使用二维数组。
现在又提出一个需求：我要存储一组数据，
1 2 3
4 5 6
7 8 9，然后把它遍历输出数据，然后把5改成10，再遍历输出。
一维数组和二维数组的声明和使用都是一样的：
1.声明数组（确定数据类型和数组名称）；
2.为数组分配空间（确定行的长度和列的长度）；
3.赋值（确定数据）；
4.数组的使用（可修改数据等）。
1.二维数组的声明
同样的，声明二维数组也有两种方式，数据类型[] [] 数组名，以及数据类型 数组名 [] []，依旧推荐使用第一种。
//声明一个int类型的二维数组，取名为arr
int [][] arr;
2.为二维数组分配空间
可以看到数据有三行三列：
//为二维数组分配3行3列的空间
arr = new int[3][3];
注意点：（同一维数组）
声明的是什么类型就必须分配什么类型的空间！否则程序会报错！
也必须分配空间！否则也会报错！
直接打印数组名，输出的是该数组的hashCode（哈希码值），即地址。
3.边声明边分配空间
二维数组也可以边声明边分配空间：
int[][] arr = new int[3][3];
4.为二维数组赋值
二维数组的本质其实还是一维数组，可以通过下面这张图简单的理解一下：
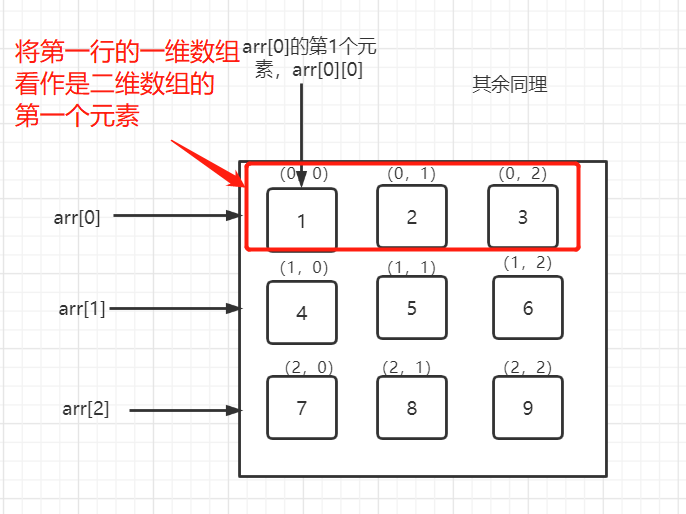
此处的注意点为：二维数组的行和列的下标都是从0开始的！
其实可以简单的理解为，第几行第几列的数据，下标都是那个几-1。
因为二维数组中的每一个元素都要赋值，所以我们可以采用遍历的方式赋值。
二维数组的行数：二维数组.length
所以我们先确定二维数组元素的长度，再每行每行的按照一维数组的遍历去遍历
二维数组中每行的长度：二维数组[下标].length
知道这两点，就可以遍历赋值了
//为二维数组赋值
int num = 1;
for(int i = 0;i<arr.length;i++){
for(int j = 0;j<arr[i].length;j++){
arr[i][j] = num;
num++;
}
}
5.边声明边分配空间边赋值
二维数组同样也可以边声明边分配空间：这种方式支持非矩形类型的二维数组，因为每一行的数据长度可以是不一样的。
//每一行放在{}中
int[][] arr = {{1,2,3},{4,5,6},{7,8,9}}
//所以{}中的数据个数可以任意，但是如果直接分配了列的空间，就每一行的列都固定了
//像int[][] arr = new int[3][3];就确定了每一列都是3个数
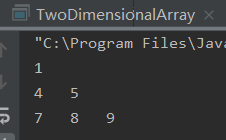
int[][] arr = {{1},{4,5},{7,8,9}} //此时第一行为一个数据，第二行为2个数据，第三行为3个数据
//此时该二维数组如下：
/*
1
4 5
7 8 9
*/
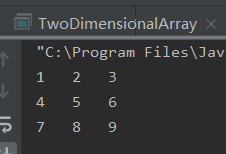
6.遍历二维数组
上述已经介绍了如何遍历二维数组，此处就来输出验证一下：
//遍历二维数组
for(int i = 0;i<arr.length;i++){ //行
for(int j = 0;j<arr[i].length;j++){ //列
System.out.print(arr[i][j]+"\t"); //按照行列输出
}
System.out.println(); //每输出一行就换行
}
7.操作二维数组
我们要将5变成10，首先要确定5的位置在第几行第几列（这里所说的几是从1开始的），我们看到，5在第2行第2列，所以它的下标就为（2-1，2-1），即（1，1）。
//操作二维数组的数据
arr[1][1] = 10;
8.for增强遍历二维数组
一维数组可以使用for增强遍历，我们说过，二维数组的本质也是一维数组，而且我们遍历的时候也是以每行的一维数组来遍历的，所以二维数组也是可以使用for增强来遍历的。
语法：
for（数据类型 自定义名字1：二维数组名）{
for（数据类型 自定义名字2：自定义名字1){
System.out.print(自定义名字1+"\t");
}
换行System.out.println();
}
//for增强遍历二维数组
for (int[] ints : arr) {
for (int anInt : ints) {
System.out.print(anInt+"\t");
}
System.out.println();
}
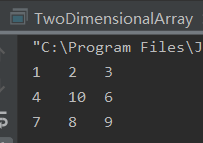
可以看到，操作数据成功~遍历也成功！
水平有限，若有错误，请指出，感激不尽~
