DS博客作业04--图

| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
| 姓名 | 邓宏 |

0.PTA得分截图

1.本周学习总结（6分）

1.1 图的存储结构

1.1.1 邻接矩阵

邻接矩阵的结构体定义

typedef struct  			
{  int edges[MAXV][MAXV]; 	/*邻接矩阵*/
   int n,e;  			/*顶点数、弧数*/
} MGraph;

建图函数

void CreateMGraph(MGraph& g, int n, int e)//建图 
{
    int a, b;
    //初始化矩阵
    for (int i = 1; i <= MAXV; i++) {
        for (int j = 1; j <= MAXV; j++) {
            g.edges[i][j] = 0;
        }
    }
    //填入对应
    for (int i = 1; i <= e; i++) {
        cin >> a >> b;
        g.edges[a][b] = 1;//无向图需要两个边都为一
        g.edges[b][a] = 1;
    }
    g.e = e;
    g.n = n;
}

1.1.2 邻接表

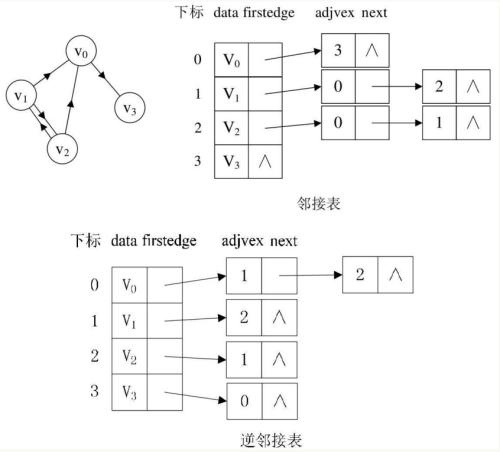
邻接矩阵的结构体定义

typedef struct ANode
{
	int adjvex;			//该边的终点编号
	struct ANode* nextarc;	//指向下一条边的指针
	int info;	//该边的相关信息，如权重
} ArcNode;				//边表节点类型
typedef int Vertex;
//声明邻接表头节点类型
typedef struct Vnode
{
	Vertex data;			//顶点信息
	ArcNode* firstarc;		//指向第一条边
} VNode;				//邻接表头节点类型
typedef VNode AdjList[MAXV];
//声明图邻接表类型
typedef struct
{
	AdjList adjlist;		//邻接表
	int n, e;		//图中顶点数n和边数e
} AdjGraph;

建图函数

void CreateAdj(AdjGraph& G, int n, int e) //创建图邻接表
{
int a, b;
ArcNode p;
G = new AdjGraph;
//初始化
for (int i = 0; i < n; i++)G->adjlist[i].firstarc = NULL;

for (int i = 1; i <= e; i++) {
    cin >> a >> b;
    //建立a与b之间的关系
    p = new ArcNode;
    p->adjvex = b;
    p->nextarc = G->adjlist[a].firstarc;
    G->adjlist[a].firstarc = p;
    //建立b与a之间的关系
    p = new ArcNode;
    p->adjvex = a;
    p->nextarc = G->adjlist[b].firstarc;
    G->adjlist[b].firstarc = p;
}
G->n = n; G->e = e;

}

1.1.3 邻接矩阵和邻接表表示图的区别

对于一个具有n个顶点e条边的无向图
它的邻接表表示有n个顶点表结点2e个边表结点
对于一个具有n个顶点e条边的有向图
它的邻接表表示有n个顶点表结点e个边表结点
如果图中边的数目远远小于n2称作稀疏图，这是用邻接表表示比用邻接矩阵表示节省空间;
如果图中边的数目接近于n2,对于无向图接近于n*(n-1)称作稠密图,考虑到邻接表中要附加链域，采用邻接矩阵表示法为宜。
故邻接矩阵适合稠密图,时间复杂度为O(n^2)
链表存储数据，适合稀疏图，时间复杂度为O(nlogn)

1.2 图遍历

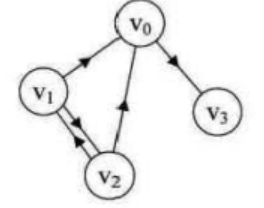
1.2.1 深度优先遍历

深度优先遍历顺序（v1开始）：v1->v2->v0->v3

深度遍历代码

//邻接矩阵
void DFS(MGraph g, int v)//深度遍历 
{
    int i;
    //控制空格输出
    if (flag==0) {
        cout << v;
        flag = 1; 
    }
    else cout << " " << v;
    visited[v] = 1;//标记已经走过的点
    
    for (i = 1; i <= g.n; i++) {
        if (g.edges[v][i]&&!visited[i]) DFS(g, i);
    }
}
//邻接表
void DFS(AdjGraph* G, int v)//v节点开始深度遍历 
{
    ArcNode* p;
    visited[v] = 1;//置已访问标记
    //控制空格输出
    if (flag == 0) {
        cout << v; 
        flag = 1;
    }
    else cout << " " << v;
    
    p=new ArcNode;//用于遍历v后面的链表
    p = G->adjlist[v].firstarc;
    while (p != NULL){
        if (!visited[p->adjvex])
            DFS(G, p->adjvex);
        p = p->nextarc;
    }
}

适用案例如：
是否有简单路径?

#include <stdio.h>
#include <malloc.h>
#include "graph.h"
int visited[MAXV];     //定义存放节点的访问标志的全局数组
void ExistPath(ALGraph *G,int u,int v, bool &has)
{
    int w;
    ArcNode *p;
    visited[u]=1;
    if(u==v)
    {
        has=true;
        return;
    }
    p=G->adjlist[u].firstarc;
    while (p!=NULL)
    {
        w=p->adjvex;
        if (visited[w]==0)
            ExistPath(G,w,v,has);
        p=p->nextarc;
    }
}

void HasPath(ALGraph *G,int u,int v)
{
    int i;
    bool flag = false;
    for (i=0; i<G->n; i++)
        visited[i]=0; //访问标志数组初始化
    ExistPath(G,u,v,flag);
    printf(" 从 %d 到 %d ", u, v);
    if(flag)
        printf("有简单路径\n");
    else
        printf("无简单路径\n");
}

int main()
{
    ALGraph *G;
    int A[5][5]=
    {
        {0,0,0,0,0},
        {0,0,1,0,0},
        {0,0,0,1,1},
        {0,0,0,0,0},
        {1,0,0,1,0},
    };  //请画出对应的有向图
    ArrayToList(A[0], 5, G);
    HasPath(G, 1, 0);
    HasPath(G, 4, 1);
    return 0;
}

问题：假设图G采用邻接表存储，设计一个算法，判断顶点u到v是否有简单路径。

1.2.2 广度优先遍历

广度优先遍历结果(v1开始)：v1->v0->v2->v3

广度遍历代码

//邻接矩阵
void BFS(MGraph g, int v)//广度遍历 
{
    int f = 0,r=0,k;
    int que[MAXV*5];//队列辅助

    //控制空格的输出
    if (flag) {
        cout << v;
        flag = 0;
    }
    visited[v] = 1;//标记已经走过的点
    
    que[r++] = v;
    while (f!=r) {
        k = que[f++];
        for (int j = 1; j <= g.n; j++) {
            if (g.edges[k][j] && !visited[j]) {
                cout << " " << j;
                visited[j] = 1;
                que[r++] = j;
            }
        }
    } 
}

//邻接表
void BFS(AdjGraph* G, int v) //v节点开始广度遍历 
{
    queue<int> q;
    int w;
    ArcNode* p;
    q.push(v);//第一个结点入队列
    visited[v] = 1; 
    cout << v;

    while (!q.empty()) {
        w = q.front();//访问队头
        q.pop();
        p = new ArcNode;
        p = G->adjlist[w].firstarc;//访问w第一条边
        while (p != NULL){
            w = p->adjvex;//边的邻接点
            if (!visited[w]){ // 若当前邻接点未被访问
               q.push(w);//该顶点进队
               visited[w] = 1;//置已访问标记
               cout << " " << w;
            }
            p = p->nextarc; //找下一个邻接点
        }
    }
}

适用案例如：
广度优先求解迷宫问题最短路径

include<Queue.h>

#pragma once

#define MaxSize 100

typedef struct

{

    int i, j;    //方块在地图中的位置

    int pre; //该路径中上一个方块在队列中的下标

}Box;    //方块类型

 

typedef struct

{

    Box data[MaxSize];

    int front, rear;

}Queue;      //用于存放路径的队列

 

void InitQueue(Queue *& q)

{

    q = (Queue *)malloc(sizeof(Queue));

    q->front = q->rear = -1;

}

 

void DestroyQueue(Queue *&q)

{

    free(q);

}

 

bool QueueEmpty(Queue *q)

{

    return (q->front == q->rear);

}

 

bool enQueue(Queue *& q, Box e)

{

    if (q->rear == MaxSize - 1)

         return false;

    q->rear++;

    q->data[q->rear] = e;

    return true;

}

 

bool deQueue(Queue *& q, Box & e)

{

    if (q->rear == q->front)

         return false;

    q->front++;

    e = q->data[q->front];

    return true;

}



cpp：

#include <iostream>

#include "Queue.h"

#define M 8

#define N 8

using namespace std;

 

int map[M + 2][N + 2] = {  //地图，1为不可走，0为可走

{1,1,1,1,1,1,1,1,1,1},{1,0,0,1,0,0,0,1,0,1},{1,0,0,1,0,0,0,1,0,1},{1,0,0,0,0,1,1,0,0,1},{1,0,1,1,1,0,0,0,0,1},

{1,0,0,0,1,0,0,0,0,1},{1,0,1,0,0,0,1,0,0,1},{1,0,1,1,1,0,1,1,0,1},{1,1,0,0,0,0,0,0,0,1},{1,1,1,1,1,1,1,1,1,1}

};

 

 

void ShowPath(Queue *qu, int front)     //输出正确路径

{

    int p = front, p0;

    do

    {

         p0 = p;

         p = qu->data[p].pre;

         qu->data[p0].pre = -1;//将正确路径的pre记为-1用以标记

    } while (p != 0); //利用循环反向找出正确路经

    cout << "最短路径：" << endl;

    for (int k = 0; k < MaxSize; k++)

    {

         if (qu->data[k].pre == -1)

         {

             cout << "(" << qu->data[k].i << "," << qu->data[k].j << ")";

             cout << "->";

         }

    }

}

 

bool Path(int x0, int y0, int x, int y) //广度优先找最优解

{

    int i, j, i0, j0; //i,j存储当前方块位置，i0,j0存储找到新路径的位置

    Box e;   //当前方块

    Queue * qu;

    InitQueue(qu);

    e.i = x0;    //设置起点位置

    e.j = y0;

    e.pre = -1;  //起点pre设置为-1;

    enQueue(qu, e);   //起点入队

    map[x0][y0] = -1; //走过的点记为-1，表示不可再走

    while (!QueueEmpty(qu))        //队非空时循环

    {

         deQueue(qu, e);       //出队，用e存储

         i = e.i; //记录该点坐标

         j = e.j;

         if (i == x && j == y)

         {

             ShowPath(qu, qu->front);  //打印路径

             DestroyQueue(qu);

             return true;

         }

         for (int circle = 0; circle < 4; circle++)  //遍历周围的方块，若方块可走就将其进队

         {

             switch (circle)   //遍历顺序为：上，右，下，左

             {

             case 0:

                  i0 = i - 1;

                  j0 = j;

                  break;

             case 1:

                  i0 = i;

                  j0 = j + 1;

                  break;

             case 2:

                  i0 = i + 1;

                  j0 = j;

                  break;

             case 3:

                  i0 = i;

                  j0 = j - 1;

                  break;

             }

             if (map[i0][j0] == 0) //移动至新位置

             {

                  e.i = i0;

                  e.j = j0;

                  e.pre = qu->front;    //用pre记录队列的数据下标

                  enQueue(qu, e);

                  map[i0][j0] = -1;

             }

         }

    }

    DestroyQueue(qu); //若队为空，说明遍历所有可以到达的方块后依旧找不到出口，即为无解

    return false;

}

 

int main()

{

    if (!Path(1, 1, 8, 8))

         cout << "迷宫无正确路径";

    return 0;

}

1.3 最小生成树

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树可以用kruskal（克鲁斯卡尔）算法或Prim（普里姆）算法求出。

1.3.1 Prim算法求最小生成树

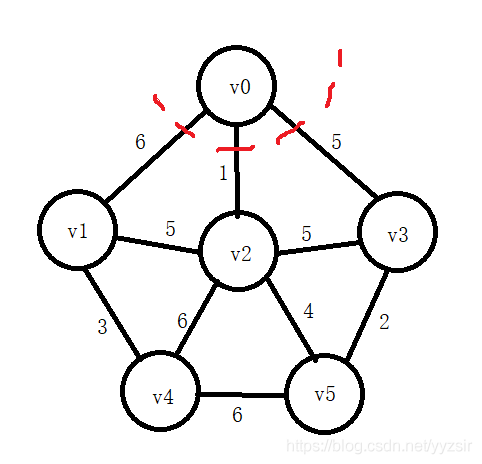
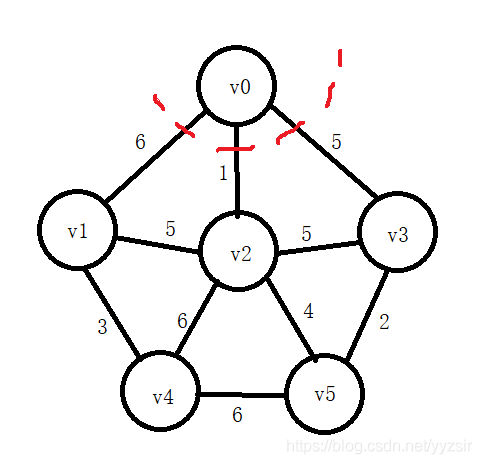
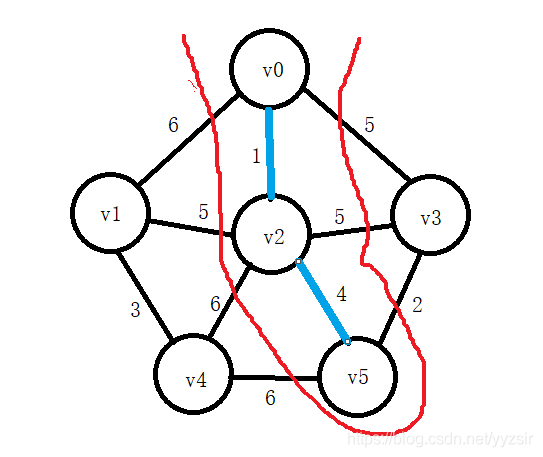
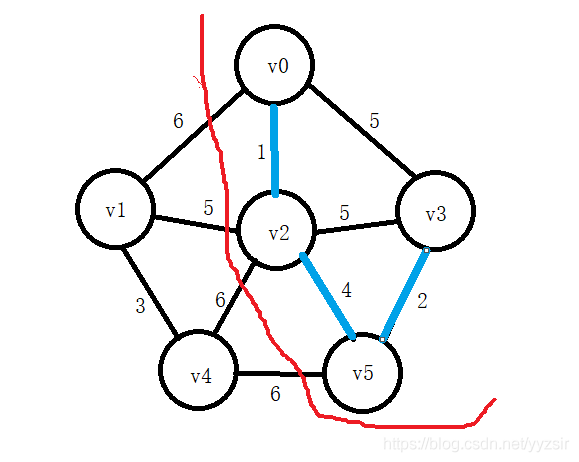
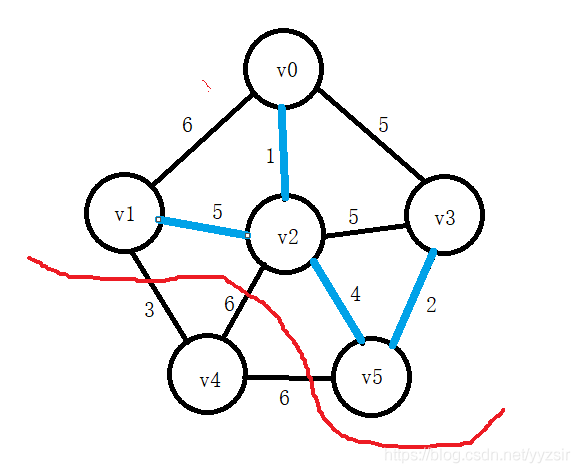
代码实现：

void Prim(MGraph g, int v)
{
    int lowcost[MAXV], min, closest[MAXV],k;
    for (int i = 0; i < g.n; i++) {//初始化lowcost与closest
        lowcost[i] = g.edges[v][i];
        closest[i] = v;
    }
    for (int i = 1; i < g.n; i++) { //找出（n-1）个顶点
        min = INF;
        for (int j = 0; j < g.n; j++) {//V-U中找出离U最近的顶点k
            if (lowcost[j] != 0 && lowcost[j] < min) {
                min = lowcost[j];
                k = j;//k记录最近顶点的编号
            }
        }
        printf("边(%d,%d)权为:%d\n", closest[k], k, min);
        lowcost[k] = 0;//标记k已经加入U
        
        for (int j = 0; j < g.n; j++) {//修改数组lowcost和closest
            if (g.edges[k][j] != 0 && g.edges[k][j] < lowcost[j]) {
                lowcost[j] = g.edges[k][j];
                closest[j] = k;
            }
        }
    }
    
}

实现Prim算法的2个辅助数组是什么？其作用是什么？Prim算法代码。
辅助数组：
1.closest保存路径
2.lowest存储一点到各点间的距离，同时判断顶点是否加入U集合
Prim算法中有两重for循环，时间复杂度为O(n^2),由于他执行时间与图中边数e关系无关,所以特别适合稠密图求最小生成树

1.3.2 Kruskal算法求解最小生成树

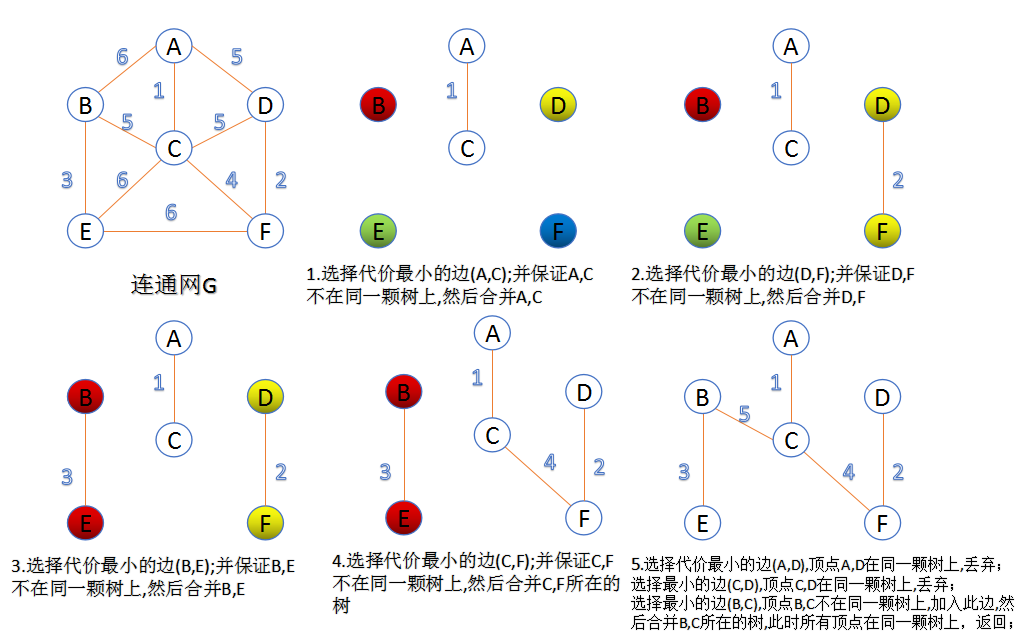
void Kruskal(AdjGraph *g)
{
    int u1, v1, sn1, sn2, k=1,j;
    int vset[MAXV];//集合辅助数组
    UFSTree t[MAXV];//并查集，树结构
    Edge E[MAXV];//存放所有边
    ArcNode* p;
    p = new ArcNode;
    for (int i = 0; i < g->n; i++) {
        p = g->adjlist[i].firstarc;
        while (p != NULL) {
            E[k].u = i;
            E[k].v = p->adjvex;
            E[k].w = p->weight;
            k++; p = p->nextarc;
        }
    }
    sort(E, E + g->n,cmp);//利用快排sort进行权值递增排序
    MakeSet(t, g->n);//初始化并查集树t
    k = 1; //k表示当前构造的树是第几条边
    j = 1;
    while (k < g->n) {
        u1 = E[j].u;
        v1 = E[j].v;
        sn1 = FindSet(t, u1);
        sn2= FindSet(t, v1);//得到两个顶点所属集合
        if (sn1 != sn2) {//集合不同
            printf("(%d,%d):%d\n", u1, v1, E[j].w);
            k++;//生成边数+1
            Union(t, u1, v1);//将两个顶点合并
        }
        j++;//进行下一条边
    }
}

采用邻接矩阵，目的是为频繁地取一条条边的权
时间复杂度为O(elog2e),执行时间仅与图中的边数有关，与顶点数无关，故适用于稀疏图建数

1.4 最短路径

1.4.1 Dijkstra算法求解最短路径

辅助数组：
dist存储某点到各点间的最短距离
path存储各点距离最短的前驱

void Dijkstra(MGraph g,int v){
	int dist[MAXV],path[MAXV];
	int s[MAXV];
	int mindis,u;
	//dist和path数组初始化 
	for(int i=0;i<g.n;i++){
		dist[i]=g.edges[v][i];
		s[i]=0;
		if(g.edges[v][i]<INF)path[i]=v;
		else path[i]=-1;
	}
	s[v]=1;//将源点放在S中 
	for(int i=0;i<g.n;i++){
		mindis=INF;
		//找最小路径长度顶点u 
		for(int j=0;j<g.n;j++){
			if(s[j]==0&&dist[j]<mindis){
				u=j;
				mindis=dist[j];
			}
		}
		s[u]=1;//u加入S 
		for(int j=0;j<g.n;j++){//修改不在s中的顶点的距离 
			if(s[j]==0){
				if(g.edges[u][j]<INF&&dist[u]+g.edges[u][j]<dist[j]){
					dist[j]=dist[u]+g.edges[u][j];
					path[j]=u;
				}
			}
		}
	}
	Dispath(dist,path,s,g.n,v);//输出 
}

时间复杂度为O(n^2),采用邻接矩阵表示

1.4.2 Floyd算法求解最短路径

void Floyd(MGraph g){
	int A[MAXV][MAXV];
	int path[MAXV][MAXV];
	for(int i=0;i<g.n;i++){//初始化A与path 
		for(int j=0;j<g.n;j++){
			A[i][j]=g.edges[i][j];
			if(i!=j&&g.edges[i][j]<INF)path[i][j]=i;
			else path[i][j]=-1;
		}
	}
	for(int k=0;k<g.n;k++){
		for(int i=0;i<g.n;i++){
			for(int j=0;j<g.n;j++){
				if(A[i][j]>A[i][k]+A[k][j]){//找更短路径 
					A[i][j]=A[i][k]+A[k][j];//进行修改 
					path[i][j]=k;
				}
			}
		}
	}
}

Floyd算法可以求得任意两个顶点的最短路，
Floyd算法需要两个二维数组A[][]与path[][]辅助,
Floyd算法优势:
Dijkstra不能处理负权图，Flyod能处理负权图；
Dijkstra需要求dist数组最短路径，Flyod不需要，且代码简

1.5 拓扑排序

结构体：

typedef struct 	       	//表头结点类型
{     
      Vertex data;         	//顶点信息
      int count;           	//存放顶点入度
      ArcNode *firstarc;   	//指向第一条边
}VNode;

代码：

void Floyd(MGraph g){
	int A[MAXV][MAXV];
	int path[MAXV][MAXV];
	for(int i=0;i<g.n;i++){//初始化A与path 
		for(int j=0;j<g.n;j++){
			A[i][j]=g.edges[i][j];
			if(i!=j&&g.edges[i][j]<INF)path[i][j]=i;
			else path[i][j]=-1;
		}
	}
	for(int k=0;k<g.n;k++){
		for(int i=0;i<g.n;i++){
			for(int j=0;j<g.n;j++){
				if(A[i][j]>A[i][k]+A[k][j]){//找更短路径 
					A[i][j]=A[i][k]+A[k][j];//进行修改 
					path[i][j]=k;
				}
			}
		}
	}
}

伪代码：

void TopSort(AdjGraph* G)
{
	将count置初值0
	再将所有顶点的入度记录在count中
	遍历count
	    if count==0  进队列

	遍历队列
	    输出顶点
	    所有点count--
	   如果 count==0  进队列
}

如何用拓扑排序代码检查一个有向图是否有环路？
在排序后判断各点count是否为0

1.6 关键路径

AOE-网：

一个工程常被分为多个小的子工程，这些子工程被称为活动，在带权有向图中若以顶点表示事件，有向边表示活动，边上的权值表示该活动持续的时间，这样的图简称为AOE网。---带权有向无环图

关键路径：

关键路径是从有向图的源点到汇点的最长路径

关键活动：

关键路径中的边叫关键活动

2.PTA实验作业（4分）

2.1 六度空间（2分）

2.1.1 伪代码

void BFS(MGraph& g,int u){
	将u顶点标记
	初始化dist[u]=0记录距离
	将u进队列
	cnt++;//用来表示几个人
	while q
	  取出队头，判断距离dist是否大于6
	  循环矩阵，只要没有被标记并且有边
	  进队列,距离+1；标记已访问，cnt++
}

2.1.2 提交列表

2.1.3 本题知识点

new申请空间：new int* [MAXV + 1]
dis[]进行距离计算，visited[]进行标记

2.2 村村通或通信网络设计或旅游规划（2分）

2.2.1 伪代码

void Dijkstra(MGraph g, int v)
{
    初始化dist数组、s数组、pay数组,dist数组
    遍历图中所有节点
	    for（i = 0; i < g.n; i++）
           若s[i]！ = 0，则数组找最短路径，顶点为u

	    s[u] = 1进s
	    for（i = 0; i < g.n; i++）

	       if（g.edges[u][j].len < INF && dist[u] + g.edges[u][j].len < dist[j]）
		     则修正dist[j] = dist[u] + g.edges[u][j].len;
				   pay[j] = pay[u] + g.edges[u][j].pay;
	       else  if（路径一样长但是花费更少）
		     则修正pay[j] = pay[u] + g.edges[u][j].pay;

}

2.2.2 提交列表

2.2.3 本题知识点

最短路径Dijkstra算法

posted @ 2021-05-23 22:23 年少不知头发贵阅读(78) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

阅读排行：
· 震惊！C++程序真的从main开始吗？99%的程序员都答错了
· winform 绘制太阳，地球，月球运作规律
· 【硬核科普】Trae如何「偷看」你的代码？零基础破解AI编程运行原理
· 上周热点回顾（3.3-3.9）
· 超详细：普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人

公告

欢迎阅读『DS博客作业04--图』

昵称：年少不知头发贵
园龄： 4年5个月
粉丝： 0
关注： 0

+加关注

2025年3月

日

一

二

三

四

五

六

DS博客作业04--图

0.PTA得分截图

1.本周学习总结（6分）

1.1 图的存储结构

1.1.1 邻接矩阵

邻接矩阵的结构体定义

建图函数

1.1.2 邻接表

邻接矩阵的结构体定义

建图函数

1.1.3 邻接矩阵和邻接表表示图的区别

1.2 图遍历

1.2.1 深度优先遍历

深度遍历代码

1.2.2 广度优先遍历

广度遍历代码

1.3 最小生成树

1.3.1 Prim算法求最小生成树

1.3.2 Kruskal算法求解最小生成树

1.4 最短路径

1.4.1 Dijkstra算法求解最短路径

1.4.2 Floyd算法求解最短路径

1.5 拓扑排序

1.6 关键路径

AOE-网：

关键路径：

关键活动：

2.PTA实验作业（4分）

2.1 六度空间（2分）

2.1.1 伪代码

2.1.2 提交列表

2.1.3 本题知识点

2.2 村村通或通信网络设计或旅游规划（2分）

2.2.1 伪代码

2.2.2 提交列表

2.2.3 本题知识点

公告

搜索

常用链接

随笔档案

阅读排行榜

评论排行榜

最新评论